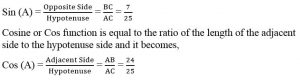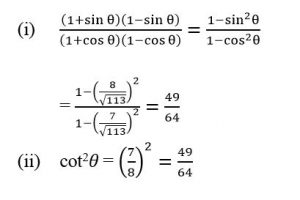TRIGNOMETRIC RATIOS:
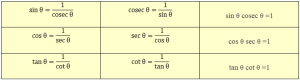
Reciprocal relation between Trigonometric Ratios:
Cosec A, sec A, and cot A are the reciprocals of sin A, cos A, and tan A respectively.
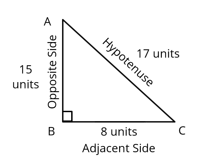
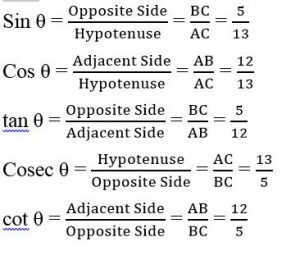
Example: Consider right triangle ABC, right angled at B. If AC = 17 units and BC = units determine all the trigonometric ratios of angle C.
Example 1. Consider right triangle ABC, right angled at B. If AC = 17 units and BC =8 units determine all the trigonometric ratios of angle C.
Solution: In Δ ABC, using Pythagoras theorem,
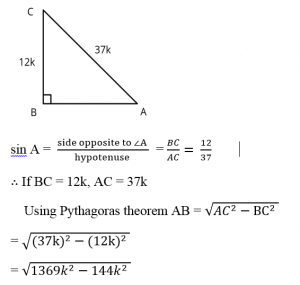
Example 2 : Given sin A = 12/37, find cos A and tan A.
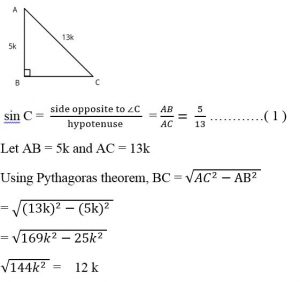
Example 3 : In ΔABC right angled at B, sin C = 5/13.
Find: (i) sin A (ii) cos A (iii) cos C.
EXERCISE 8.1
1.In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution: In a given triangle ABC, right angled at B = ∠B = 90°
Given: AB = 24 cm and BC = 7 cm
According to the Pythagoras Theorem,
In a right- angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
By applying Pythagoras theorem, we get
AC² = AB² + BC²
AC² = (24 )²+ (7)²
AC² = 576 + 49
⇒ AC² = 625 ⇒AC = 25
(i) To find Sin (A), Cos (A)
Solution. We know that Sine (Sin) function is the equal to the ratio of length of the opposite side to the hypotenuse side. So it becomes
(ii) To find Sin (C), Cos (C)
Sin (C) = AB/AC = 24/25
Cos (C) = BC/AC = 7/25
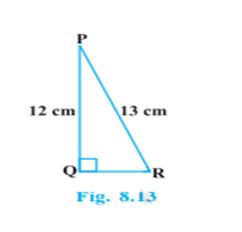
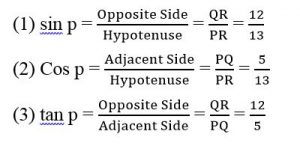
2.In Fig. 8.13, find tan P – cot R
Solution: In the given triangle PQR, the given triangle is right angled at Q and the given measures are:
PR = 13 cm, PQ = 12 cm
Since the given triangle is right angled triangle, to find the side QR, apply the Pythagoras theorem
In a right- angled triangle, the squares of the hypotenuse side is equal to the sum of the squares of the other two sides.
(PR)2 = (QR)2 + (PQ)2
Substitute the values of PR and PQ
(13)2 = (QR)2 + (12)2
169 = (QR)2 + 144
Therefore, (QR)2 = 169 − 144
(QR)² = 25 ⇒ QR = √25 = 5
Therefore, the side QR = 5 cm.
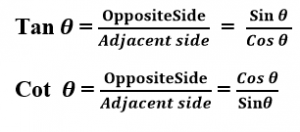
To find tan P – cot R:
tan (P) = (Opposite Side)/Hypotenuse = QR/PQ = 5/12 Since cot is the reciprocal of the tan.
Cot (R) = (Adjacent Side)/Hypotenuse = QR/PQ = 5/12
Tan (P) – cot (R) = 5/12 – 5/12 = 0
∴ tan (P) – cot(R) = 0
3. If sin A = 3/4, Calculate cos A and tan A.
Solution: Let us assume a right angled triangle ABC, right angled at B
Sin A = 3/4 ( given)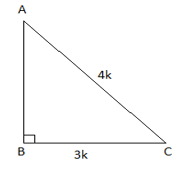
Sin A = (Opposite Side)/Hypotenuse = 3/4
Let BC be 3k and AC will be 4k
where k is a positive real number.
According to the Pythagoras theorem, we get,
(AC)2 = (AB)2 + (BC)2
Substituting the value of AC and BC
(4k)² = AB² + (3k)²
16k² − 9k² = (AB)²
(AB)² = 7k²
Therefore, AB = √7k
Now, we have to find the value of cos A and tan A
We know that,

Therefore, tan A = 3/√7
4.Given 15 cot A = 8, find sin A and sec A.
Solution: Let us assume a right angled triangle ABC, right angled at B
Given: 15 cot A = 8
So, Cot A = 8/15
Let AB be 8k and BC will be 15k where, k is a positive real number.
According to the Pythagoras theorem, we get
(AC )² = (AB)² + (BC)²
Substitute the value of AB and BC
(AC)2 = (8k)2 + (15k)2
(AC)2 = 64k2 + 225k2
(AC)2 = 289k2
Therefore, AC = 17k
Now, we have to find the value of sin A and sec A
We know that, Sin (A) = (Opposite Side)/Hypotenuse
Substitute the value of BC and AC , we get
Sin A = BC/AC = 15k/17k = 15/17
∴ Sin A = 15/17
Sec A = Hypotenuse/(Adjacent Side)
Substitute the value of BC and AB we get,
AC/AB = 17k/8k = 17/8 ∴ sec A = 17/8
5. Given sec θ = 13/12 Calculate all other trigonometric ratios
Solution: We know that sec is the reciprocal of the cos which is equal to the ratio of the length of the hypotenuse side to the adjacent side
Let us assume a right angled triangle ABC, right angled at B
sec θ = 13/12 = Hypotenuse/(Adjacent Side) = AC/AB
Let AC be 13k and AB will be 12k where, k is a positive real number.
According to the Pythagoras theorem, the squares of the hypotenuse side is equal to the sum of the squares of the other two sides of a right angle triangle and we get,
(AC)2 = (AB)2 + ( BC)2
Substitute the value of AB and AC
(13k)2 = (12k)2 + (BC)2
169k2 = 144k2 + (BC)2
169k2 = 144k2 + (BC)2
(BC)2 = 169k2 – 144k2
(BC)2 = 25k2
Therefore, BC = 5k
Now, substitute the corresponding values in all other trigonometric ratios
So,
6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠ A = ∠ B.
Solution: Let us assume the triangle ABC in which CD⊥AB
Give that the angles A and B are acute angles, such that
Cos (A) = cos (B)
As per the angles taken, the cos ratio is written as
AD/AC = BD/BC
Now, interchange the terms, we get
AD/BD = AC/BC
Let take a constant value = k
Now consider the equation as
AD = k BD … (1)
AC = k BC … (2)
By applying Pythagoras theorem in △CAD and △CBD we get,
(CD)2 = (BC)2 – (BD)2 … (3)
(CD)2 = (AC)2 − (AD)2 …. (4)
From the equations (3) and (4) we get,
(AC)2 − (AD)2 = (BC)2 − (BD)2
Now substitute the equations (1) and (2) in (3) and (4)
k² [(BC)2 − (BD)2] = [(BC)2 − (BD)2] k2 = 1
Putting this value in equation, we obtain AC = BC
∠A = ∠B (Angles opposite to equal side are equal-isosceles triangle)
7. If cot θ = 7/8, evaluate :
(i) (1 + sin θ) ((1− sin θ))/(1 + cos θ)(1− cos θ) (ii) cot² θ
Solution: Let us assume a ΔABC in which ∠B = 90° and ∠C = θ
cot θ = BC/AB = 7/8 ( given)
Let BC = 7 k and AB = 8 k, where k is a positive real number
According to Pythagoras theorem in ΔABC we get.
(AC)2 = (AB)2 + (BC)2
(AC)2 = 64k2 + 49k2
AC = √113 k
According to the sine and cos function ratios, it is written as
sin θ = AB/AC = (Opposite Side)/Hypotenuse = 8k/(√113 k) = 8/√113 and
cos θ = (Adjacent Side)/Hypotenuse = BC/AC = 7k/(√113 k) = 7/√113
Now apply the values of sin function and cos function:
8.If 3 cot A = 4, check whether (1− tan2 A)/(1 + tan2A) = cos2A – sin 2 A or not.
Solution: Let ΔABC in which ∠B = 90°
We know that, cot function is the reciprocal of tan function and it is written as
cot(A) = AB/BC = ( 4)/3
Let AB = 4k an BC = 3k, where k is a positive real number.
According to the Pythagorean theorem,
(AC)² = (AB)² + (BC)²
(AC)² = (4k)² + (3k)²
(AC)² = 16k² + 9k²
(AC)² = 25k²
AC = 5k
Now, apply the values corresponding to the ratios
tan(A) = BC/AB = 3/4
sin (A) = BC/AC = 3/5
cos (A) = AB/AC = 4/5
9. In triangle ABC, right-angled at B, if tan A = 1/√3 find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution: Let ΔABC in which ∠B = 90°
tan A = 1/√3
Let BC = 1k and AB = √3 k, where k is the positive real number.
By Pythagoras theorem in ΔABC we get:
(AC) 2 = (AB) 2 + (BC) 2
(AC) 2 = (k) 2 + (k) 2
AC) 2 = (4k) 2
AC = 2k
Now find the values of cos A, Sin A
Sin A = BC/AC = 1/2
Cos A = AB/AC = √3/2
Then find the values of cos C and sin C
Sin C = AB/AC = √3/2
Cos C = BC/AC = 1/2
Now, substitute the values in the given problem
(i) sin A cos C + cos A sin C = ( 1/2 ) × ( 1/( 2) ) + √3/2 ×(√3 )/2 = 1/4 + 3/4 = 1
(ii) cos A cos C – sin A sin C = ((√3 )/2 ) ( 1/( 2)) – (1/( 2)) (( √3)/2 ) = 0
10.In ∆ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P
Solution: In a given triangle PQR, right angled at Q, the following measures are
PQ = 5 cm and PR + QR = 25 cm
Now let us assume, QR = x cms
According to the Pythagorean Theorem,
(PR)² = (PQ)² + (QR)²
Substitute the value of PR as x
(25 – x)² = 5² + x²
25² + x² – 50 x = 25 + x²
625 + x²– 50 x – 25 – x² = 0
−50 x = − 600
x = (−600)/(−50)
x = 12 = QR
Now, find the value of PR
PR = 25 − QR
Substitute the value of QR
PR = 25−12
PR = 13
Now, substitute the value to the given problem
11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 12/5 for some value of angle A.
(iii)cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 4/3 for some angle θ.
(i) Ans: False
Justification: In ΔMNC we have ∠N = 90∘, MN = 3, NC = 4 and MC = 5
Value of tan M = 4/3 which is greater than 1 .
The triangle can be formed with sides equal to 3, 4 and hypotenuse = 5 as it will follow the Pythagoras theorem.
(MC)² = (MN)² + (NC)²
5² = 3² + 4²
25 = 9 + 16 ⇒ 25 = 25
(ii) sec A = 12/5 for some value of angle A
Ans: True
Justification: Let us consider ΔMNC in which ∠N = 90º,
MC = 12k and MB = 5k, where k is a positive real number.
By Pythagoras theorem we get,
(MC)²= (MN)² + (NC)²
(12k)² = (5k)² + (NC)²
(NC)² + (25)² = (144)²
(NC)² = 119k²
Such a triangle is possible as it will follow the Pythagoras theorem.
(iii) cos A is the abbreviation used for the cosecant of angle A.
Ans: False
Justification: Abbreviation used for cosecant of angle M is cosec M. cos M is the abbreviation used for cosine of angle M.
(iv) cot A is the product of cot and A.
Ans: False
Justification: cot M is not the product of cot and M. It is the cotangent of ∠M.
(v) sin θ = 4/3 for some angle θ.
Ans: False
Justification: sin θ = Height/Hypotenuse
We know that in a right angled triangle, Hypotenuse is the longest side.
∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ