EXERCISE 10.1

Tangents to a Circle:

All the tangents of a circle are perpendicular to the radius through the point of contact of that tangent.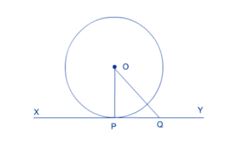

OP is the radius of the circle and Q is any point on the line XY which is the tangent to the circle. As OP is the shortest line of all the distances of the point O to the points on XY. So OP is perpendicular to XY. Hence, OP⊥ XY

Example 1 : Find the radius of the circle in the given figure, if the length of the tangent from point A which is 5 cm away from center is 4 cm.

Solution : As we know that the radius is perpendicular to the radius, so the ∆ABO is a right angle triangle.
Given, AO = 5 cm and AB = 4 cm
We can use Pythagoras theorem here
OA ²=  OB ² + AB ²
OB ²=  OA ² −  AB ²
OB ²= 5 ² − 4 ²
= 25 – 16
OB ² = 9    ⇒ OB = 3
So the radius of the given circle is 3 cm.

Exercise: 10.1

1.How many tangents can a circle have.

Solution: There can be infinite tangents to a circle. A circle is made up of infinite points which are at an equal distance from a point. Since there are infinite points on the circumference of a circle, infinite tangents can be drawn from them.

2.Fill in the blanks:

(i) A tangent to a circle intersects it in …………… point(s).

(ii) A line intersecting a circle in two points is called a ………….

(iii) A circle can have …………… parallel tangents at the most.

(iv) The common point of a tangent to a circle and the circle is called …………

Solution: (i) A tangent to a circle intersects it in one point(s).

(ii) A line intersecting a circle in two points is called a secant.

(iii) A circle can have two parallel tangents at the most.

(iv) The common point of a tangent to a circle and the circle is called the point of contact.

3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm.
Length PQ is : (A) 12 cm      (B) 13 cm       (C) 8.5 cm   (D) √119cm

Solution:

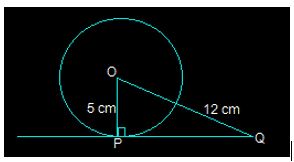
In the above figure, the line that is drawn from the centre of the given circle to the tangent PQ is perpendicular to PQ.
And so, OP ⊥ PQ
Using Pythagoras theorem in triangle ΔOPQ we get,
OQ² = OP² + PQ²
(12)² = 5²+ PQ²
PQ²= 144 − 25
PQ2 = 119  ⇒    PQ = √119 cm
So, option D.

4. Draw a circle and two lines parallel to a given line such that one is a tangent and the  other, a secant to the circle.
Solution:

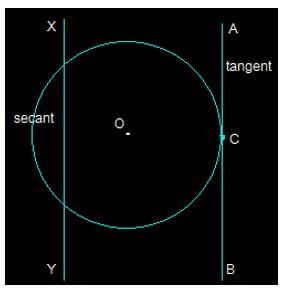
In the above figure, XY and AB are two the parallel lines. The line segment AB is the tangent at point C while the line segment XY is the secant.