ADDITIONAL QUESTIONS AND ANSWERS:
1. The length of the tangent to a circle from a point P, which is 25 cm away from the centre, is 24 cm. What is the radius of the circle?
Soln:
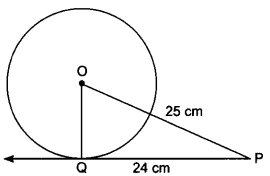
∵ OQ ⊥ PQ
∴ PQ2 + QO2 = OP2
⇒ 252 = OQ2 + 242
or OQ = √625 – √576
= √49 = 7 cm
2. In Fig. 8.6, ABCD is a cyclic quadrilateral. If ∠BAC = 50° and ∠DBC = 60° then find ∠BCD.
Soln:
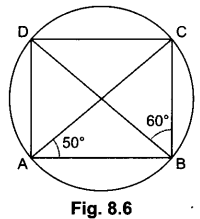
Here ∠BDC = ∠BAC = 50° (angles in same segment are equal)
In ABCD, we have
∠BCD = 180° – (∠BDC + ∠DBC)
= 180° – (50° + 60°) = 70°
3. In Fig. 8.7, the quadrilateral ABCD circumscribes a circle with centre O.
If ∠AOB = 115°, then find ∠COD.
Soln:
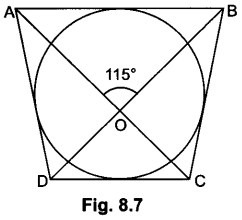
∵ ∠AOB = ∠COD (vertically opposite angles)
∴ ∠COD = 115°
4. In Fig. 8.8, AABC is circumscribing a circle. Find the length of BC.
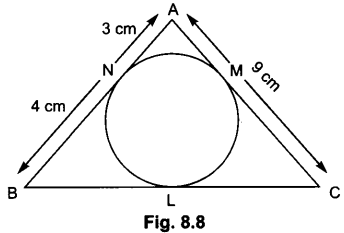
Soln:
AN = AM = 3 cm (Tangents drawn from an external point)
BN = BL = 4 cm (Tangents drawn from an external point)
CL = CM = AC – AM = 9 – 3 = 6 cm
⇒ BC = BL + CL = 4 + 6 = 10 cm.
5. In Fig. 8.9, O is the centre of a circle, PQ is a chord and the tangent PR at P
makes an angle of 50° with PQ. Find ∠POQ.
Soln:
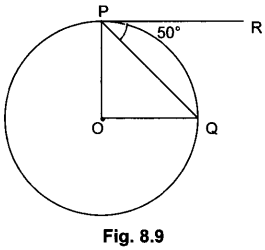
∠OPQ = 90° – 50° = 40°
OP = OQ [Radii of a circle]
∠OPQ = ∠OQP = 40°
(Equal opposite sides have equal opposite angles)
∠POQ = 180° – ∠OPQ – ∠OQP
= 180° – 40° – 40° = 100°
6. If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm,
then find the length of each tangent.
Soln:
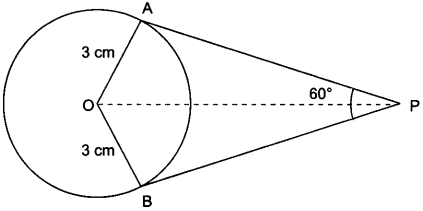
In Fig. 8.10
∆AOP ≅ ∆BOP (By SSS congruence criterion)
∠APO = ∠BPO = 60°/2 = 30°
In ∆AOP, OA ⊥ AP
∴ tan 30° = OA/AP
⇒ 1/√3 = 3/AP
⇒ AP = 3/√3 cm
7. If radii of two concentric circles are 4 cm and 5 cm, then find the length of
each chord of one circle which is tangent to the other circle.
Soln:
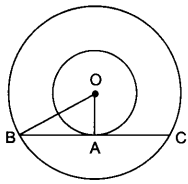
OA = 4 cm, OB = 5 cm
Also, OA ⊥ BC
∴ OB2 = OA2 + AB2
⇒ 52 = 42 + AB2
⇒ AB = √25 – √16 = 3 cm
⇒ BC = 2 AB = 2 × 3 = 6 cm
8. The length of tangent from an external point P on a circle with centre O is always less than OP.
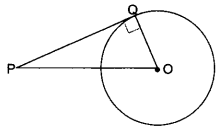
Soln:
This is true, let PQ be the tangent from the external point P.
Then ∆PQO is always a right angled triangle with OP as the hypotenuse.
So, PQ is always less than OP.
9. If angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre 0 is 90°, then OP = a√2.
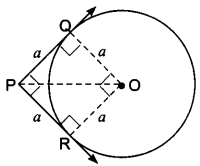
Soln:
True, let PQ and PR be the tangents
Since ∠P = 90°, so ∠QOR = 90°
Also, OR = OQ = a
∴ PQOR is a square
![]()
10. In Fig. 8.20, PA and PB are tangents to the circle drawn from an external point P. CD is the third tangent touching the circle at Q. If PA = 15 cm, find the perimeter of ∆PCD.
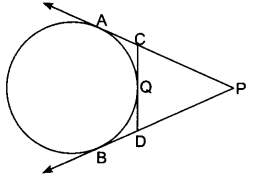
Soln:
∵ PA and PB are tangent from same external point
∴ PA = PB = 15 cm
Now, Perimeter of ∆PCD = PC + CD + DP = PC + CQ + QD + DP
= PC + CA + DB + DP
= PA + PB = 15 + 15 = 30 cm
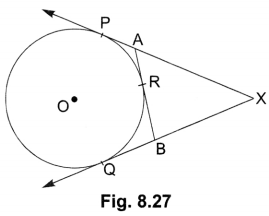
Soln:
In the given figure,
AP = AR
BR = BQ
XP = XQ (tangents to a circle from an external point are equal)
XA + AP = XB + BQ
XA + AR = XB + BR (AP = AR, BQ = BR)
12. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre 0 at a point so that OQ = 12 cm. Find the length of PQ.
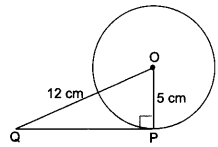
Soln:
We have, ∠OPQ = 90°
OQ = 12 cm and OP = 5 cm
∴ By Pythagoras Theorem
OQ2 = OP2 + QP2
⇒ 122 = 52 + QP2
⇒ QP2 = 144 – 25 = 119
= QP = √119 cm
13. From a point l, the length of the tangent to a circle is 24 cm and the distance
of Q from the centre is 25 cm. Find the radius of the circle.
Soln:
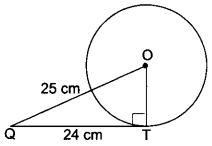
Let QT be the tangent and OT be the radius of circle. Therefore
OT ⊥ QT i.e., ∠OTQ = 90°
and OQ = 25 cm and QT = 24 cm
Now, by Pythagoras Theorem, we have
OQ2 = QT2 + OT2
⇒ 252 = 242 + OT2
⇒ OT2 = 252 – 242
⇒ 625 – 576
OT2 = 49 ⇒ OT = 7 cm
14. In Fig. 8.35, if TP and TQ are the two tangents to a circle with centre O
so that ∠POQ = 110°, then find ∠PTQ.
Soln:
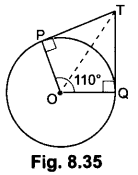
Since TP and TQ are the tangents to the circle with centre O
So, OPIPT and OQ ⊥ QT
⇒ ∠OPT = 90°, ∠OQT = 90° and ∠POQ = 110°
So, in quadrilateral OPTQ, we have
∠POQ + ∠OPT + ∠PTQ + ∠TQO = 360°
⇒ 110° + 90° + ∠PTQ + 90° = 360°
⇒ ∠PTQ + 290° = 360°
∴ ∠PTQ = 360° – 290°
= ∠PTQ = 70°
15. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Soln:
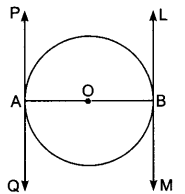
Let AB be the diameter of the given circle with centre O, and two tangents PQ and LM are drawn at the end of diameter AB respectively.
Р. Now, since the tangent at a point to a circle is perpendicular to the radius through the point of contact.
Therefore, OA ⊥ PQ and OB ⊥ LM
i.e., AB ⊥ PQ and also AB ⊥ LM
⇒ ∠BAQ = ∠ABL (each 90°)
∴ PQ||LM (∵ ∠BAQ and ∠ABL are alternate angles)
16. The length of a tangent from a point A at distance 5 cm from the centre of the
circle is 4 cm. Find the radius of the circle.
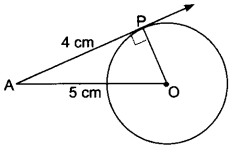
Soln:
Let O be the centre and P be the point of contact.
Since tangent to a circle is perpendicular to the radius through the point of contact,
∴ ∠OPA = 90° Now, in right ∆OPA we have
OA2 = OP2 + PA2 (By Pythagoras Theorem)
52 = OP2 + 42
= 25 = OP2 + 16
⇒ OP2 = 25 – 16 = 9
∴ OP = 3 cm
Hence, the radius of the circle is 3 cm.
17. If a point P is 17 cm from the centre of a circle of radius 8 cm, then find the length of the tangent drawn to the circle from point P.
Soln:
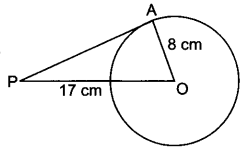
OA ⊥ PA (∵ radius is ⊥ to tangent at point of contact)
∴ In ∆OAP, we have
PO2 = PA2 + AO2
⇒ (17)2 = (PA)2 + (8)2
(PA)2 = 289 – 64 = 225
⇒ PA = √225 = 15
Hence, the length of the tangent from point P is 15 cm.
18. PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120° then find ∠OPQ.
Soln:
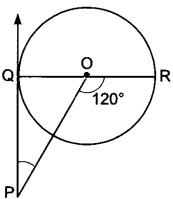
∠OQP = 90°
∠QOP = 180° – 120° = 60°
∠OPQ = 180° – ∠OQP – ∠QOP
= 180° – 90° – 60°
= 30°
19. AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
Soln:
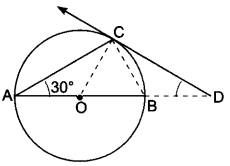
Join OC,
∠ACB = 90° (Angle in semi-circle)
∴ ∠OBC = 180° – (90° + 30°) = 60°
Since, OB = OC = radii of same circle
∴ ∠OBC = ∠OCB = 60°
Also, ∠OCD = 90°
⇒ ∠BCD = 90° – 60° = 30°
Now, ∠OBC = ∠BCD + ∠BDC (Exterior angle property)
⇒ 60° = 30° + ∠BDC
⇒ ∠BDC = 30°
∵ ∠BCD = ∠BDC = 30°
∴ BC = BD
20. In Fig. 8.20, PA and PB are tangents to the circle drawn from an external point P. CD is the third tangent touching the circle at Q. If PA = 15 cm, find the perimeter of ∆PCD.

Soln:
∵ PA and PB are tangent from same external point
∴ PA = PB = 15 cm
Now, Perimeter of ∆PCD = PC + CD + DP = PC + CQ + QD + DP
= PC + CA + DB + DP
= PA + PB = 15 + 15 = 30 cm
21. In Fig. 8.21, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
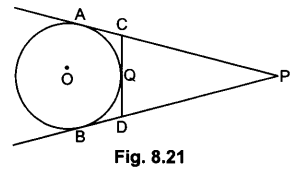
Soln:
PA = PC + CA = PC + CQ [∵ CA = CQ (tangents drawn An from external point are equal)]
⇒ 12 = PC + 3 = PC = 9 cm
∵ PA = PB = PA – AC = PB – BD
⇒ PC = PD
∴ PD = 9 cm
Hence, PC + PD = 18 cm
22. In Fig. 8.28, a circle is inscribed in a AABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF.
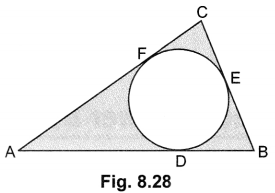
Soln:
Let AD = AF = x
∴ DB = BE = 12 – x
and CF = CE = 10 – x
BC = BE + EC
⇒ 8 = 12 – x + 10 – x
⇒ x = 7
∴ AD = 7 cm, BE = 12 – 7 = 5 cm, CF = 10 – 7 = 3 cm
23. In Fig. 8.30 from an external point P, two tangents PT and PS are drawn to a circle with centre 0 and radius r. If OP = 2r, show that ∠OTS = ∠OST = 30°.
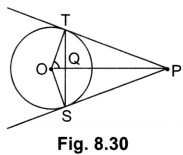
Soln:
Let ∠TOP = θ
∴ cos θ = OT/OP = r/2r =1/2
⇒ cos θ = cos 60°
⇒ θ = 60°
Hence, ∠TOS = 120°
In ∆OTS, OT = OS [Radii of circle]
⇒ ∠OTS = ∠OST = 60÷2 = 30°
