Construction of Tangents to a Circle.
Tangent is a line which intersects the circle at one point only at the outer of the circle. It is always perpendicular to the radius of the circle.
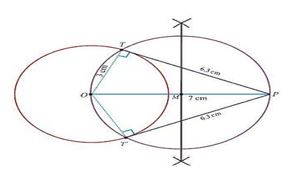
Example : Construct the pair of tangents to the circle of radius 3 cm from the point which is 7 cm away from its centre, and measure their lengths also.
Steps of Construction:
Step 1: Draw a circle of radius 3 cm by taking O as the centre.
Step 2: Mark a point P outside the circle at a distance of 7 cm from the centre O. Join OP.
Step 3: Bisect the line segment OP, so that the perpendicular bisector of OP intersects it at the point M.
Step 4: Now draw another circle by taking M as centre and MO as radius, which intersects the given circle at two points’ i.e. T and Tꞌ.
Step 5: Now join PT and PT’ which are the required tangents and measure the length of the tangents.
The length of the tangents is PT = PTꞌ = 6.3 cm.
EXERCISE 11.2
In each of the following, give the justification of the construction also:
1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Construction Procedure:
The construction to draw a pair of tangents to the given circle is as follows.
1.Draw a circle with radius = 6 cm with centre O.
2. Locate a point P, which is 10 cm away from O.
3. Join the points O and P through line
4. Draw the perpendicular bisector of the line OP.
5. Let M be the mid-point of the line PO.
6. Take M as centre and measure the length of MO
7. The length MO is taken as radius and draw a circle.
8. The circle drawn with radius = MO, intersect the previous circle at point Q and R.
9. Join PQ and PR.
10. Therefore, PQ and PR are the required tangents.
Justification: The construction of the given problem can be justified by proving that PQ and PR are the tangents to the circle of radius 6cm with centre O.
To prove: Join OQ and OR represented in dotted lines.
From the construction, ∠ PQO is an angle in the semi-circle.
We know that angle in a semi-circle is a right angle, so it becomes,
∴ ∠ PQO = 90°
Such that ⇒ OQ ⊥ PQ
Since OQ is the radius of the circle with radius 6 cm, PQ must be a tangent of the circle. Similarly, we can prove that PR is a tangent of the circle.
Hence, justified.
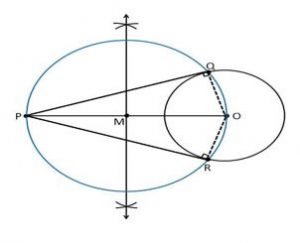
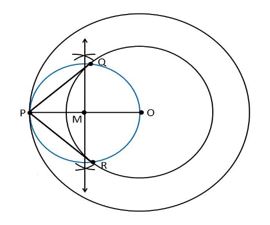
2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Construction Procedure:
For the given circle, the tangent can be drawn as follows.
1.Draw a circle of 4 cm radius with centre “O”.
2. Again, take O as centre draw a circle of radius 6 cm.
3. Locate a point P on this circle
4. Join the points O and P through lines such that it becomes OP.
5. Draw the perpendicular bisector to the line OP6. Let M be the mid-point of PO.
7. Draw a circle with M as its centre and MO as its radius
8. The circle drawn with radius = OM, intersect the given circle at the points Q and R.
9. Join PQ and PR.
10. PQ and PR are the required tangents.
From the construction, it is observed that PQ and PR are of length 4.47 cm each.
It can be calculated manually as follows
Since PQ is a tangent,
Applying Pythagoras theorem in ∆PQO, we get
(PQ)² + (QR)² = (PO)²+ (4)2 = (6)2
PQ2 +16 = 36
PQ2 = 36 −16 ⇒ PQ2 = 20
PQ = 2 √5 ⇒ PQ = 4.47 cm
Therefore, the tangent length PQ = 4.47
Justification: The construction of the given problem can be justified by proving that PQ and PR are the tangents to the circle of radius 4 cm with centre O.
To prove this, join OQ and OR represented in dotted lines.
From the construction,
∠ PQO is an angle in the semi-circle.
We know that angle in a semi-circle is a right angle, so it becomes,
∴ ∠ PQO = 90°
Such that ⇒ OQ ⊥ PQ
Since OQ is the radius of the circle with radius 4 cm, PQ must be a tangent of the circle. Similarly, we can prove that PR is a tangent of the circle.
Hence, justified.
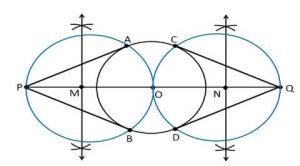
3. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Construction Procedure:
The tangent for the given circle can be constructed as follows.
1. Draw a circle with a radius of 3cm with centre “O”.
2. Draw a diameter of a circle and it extends 7 cm from the centre and mark it as P and Q.
3. Draw the perpendicular bisector of the line PO and mark the midpoint as M.
4. Draw a circle with M as centre and MO as radius
5. Now join the points PA and PB and the circle with radius MO intersects the circle of 3 cm.
6. Now PA and PB are the required tangents.
7. Similarly, from the point Q, we can draw the tangents.
8. From that, QC and QD are the required tangents.
Justification: The construction of the given problem can be justified by proving that PQ and PR are the tangents to the circle of radius 3 cm with centre O.
To prove this, join OA and OB.
From the construction,
∠PAO is an angle in the semi-circle.
We know that angle in a semi-circle is a right angle, so it becomes,
∴ ∠PAO = 90°
Such that ⇒ OA ⊥ PA
Since OA is the radius of the circle with radius 3 cm, PA must be a tangent of the circle. Similarly, we can prove that PB, QC and QD are the tangent of the circle.
Hence, justified.
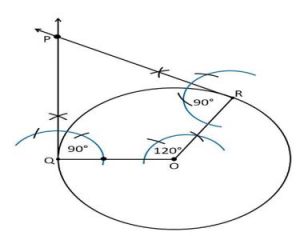
4. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°
Construction Procedure:
The tangents can be constructed in the following manner:
1. Draw a circle of radius 5 cm and with centre as O.
2. Take a point Q on the circumference of the circle and join OQ.
3. Draw a perpendicular to QP at point Q.
4. Draw a radius OR, making an angle of 120° (180°−60°) with OQ.
5. Draw a perpendicular to RP at point R.
6. Now both the perpendiculars intersect at point P.
7. Therefore, PQ and PR are the required tangents at an angle of 60°.
Justification: The construction can be justified by proving that ∠ QPR = 60°
By our construction
∠ OQP = 90° and ∠ ORP = 90°
And ∠ QOR = 120°
We know that the sum of all interior angles of a quadrilateral = 360°
∠ OQP + ∠ QOR + ∠ ORP +∠ QPR = 360o
90° + 120° + 90° + ∠ QPR = 360°
Therefore, ∠QPR = 60°
Hence Justified.
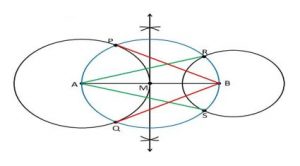
5. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm.Construct tangents to each circle from the centre of the other circle.
Construction Procedure:
The tangent for the given circle can be constructed as follows.
1. Draw a line segment AB = 8 cm.
2. Take A as centre and draw a circle of radius 4 cm
3. Take B as centre, draw a circle of radius 3 cm
4. Draw the perpendicular bisector of the line AB and the midpoint is taken as M.
5. Now, take M as centre draw a circle with the radius of MA or MB which the intersects the circle at the points P, Q, R and S.
6. Now join AR, AS, BP and BQ
7. Therefore, the required tangents are AR, AS, BP and BQ
Justification: The construction can be justified by proving that AS and AR are the tangents of the circle (whose centre is B with radius is 3 cm) and BP and BQ are the tangents of the circle (whose centre is A and radius is 4 cm).
From the construction, to prove this, join AP, AQ, BS, and BR.
∠ASB is an angle in the semi-circle.
∴ ∠ASB = 90° (angle in a semi-circle is a right angle)
⇒ BS ⊥ AS
Since BS is the radius of the circle, AS must be a tangent of the circle.
Similarly, AR, BP, and BQ are the required tangents of the given circle.
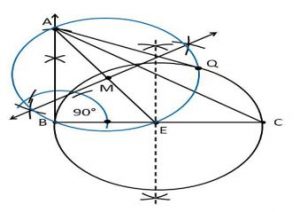
6. Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠ B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Construction Procedure:
The tangent for the given circle can be constructed as follows
1. Draw the line segment with base BC = 8cm
2. Measure the angle 90° at the point B, such that ∠ B = 90°.
3. Take B as centre and draw an arc with a measure of 6 cm.
4. Let the point be A where the arc intersects the ray.
5. Join the line AC.
6. Therefore, ABC be the required triangle.
7. Now, draw the perpendicular bisector to the line BC and the midpoint is marked as E.
8. Take E as centre and BE or EC measure as radius draw a circle.
9. Join A to the midpoint E of the circle
10. Now, again draw the perpendicular bisector to the line AE and the midpoint is taken as M
11. Take M as centre and AM or ME measure as radius, draw a circle.
12. This circle intersects the previous circle at the points B and Q
13. Join the points A and Q
14. Therefore, AB and AQ are the required tangents
Justification: The construction can be justified by proving that AG and AB are the tangents to the circle.
From the construction, join EQ.
∠AQE is an angle in the semi-circle.
∴ ∠AQE = 90° (angle in a semi-circle is a right angle)
⇒ EQ⊥ AQ
Since EQ is the radius of the circle, AQ has to be a tangent of the circle.
Similarly, ∠B = 90°
⇒ AB ⊥ BE
Since BE is the radius of the circle, AB has to be a tangent of the circle.
Hence, justified.
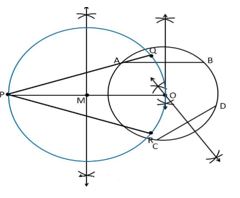
7. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Construction Procedure:
The required tangents can be constructed on the given circle as follows.
1. Draw a circle with the help of a bangle.
2. Draw two non-parallel chords such as AB and CD
3. Draw the perpendicular bisector of AB and CD
4. Take the centre as O where the perpendicular bisector intersects.
5. To draw the tangents, take a point P outside the circle.
6. Join the points O and P.
7. Now draw the perpendicular bisector of the line PO and midpoint is taken as M
8. Take M as centre and MO as radius draw a circle.
9. Let the circle intersects intersect the circle at the points Q and R
10. Now join PQ and PR
11. Therefore, PQ and PR are the required tangents.
Justification: The construction can be justified by proving that PQ and PR are the tangents to the circle.
Since, O is the centre of a circle, we know that the perpendicular bisector of the chords passes through the centre.
Now, join the points OQ and OR.
We know that perpendicular bisector of a chord passes through the centre.
It is clear that the intersection point of these perpendicular bisectors is the centre of the circle.
Since, ∠ PQO is an angle in the semi-circle.
∴ ∠ PQO = 90° (angle in a semi-circle is a right angle) ⇒ OQ⊥ PQ
Since OQ is the radius of the circle, PQ has to be a tangent of the circle. Similarly,
∴ ∠ PRO = 90°
⇒ OR ⊥ PO
Since OR is the radius of the circle, PR has to be a tangent of the circle
Therefore, PQ and PR are the required tangents of a circle.