MULTIPLE CHOICE QUESTIONS: (MCQ’s)
1. The perimeter of a circle having radius 5 cm is equal to____
(a) 30 cm
(b) 3.14 cm
(c) 31.4 cm
(d) 40 cm
2. Area of the circle with radius 5 cm is equal to_____
(a) 60 sq.cm
(b) 75.5 sq.cm
(c) 78.5 sq.cm
(d) 10.5 sq.cm
3. The largest triangle inscribed in a semi − circle of radius r, then the area of that triangle is_____
(a) r2.
(b) 1/2 r2
(c) 2 r2
(d) √2 r2
4. If the perimeter of the circle and square are equal, then the ratio of
their areas will be equal to_____
(a) 14:11
(b) 22:7
(c) 7:22
(d) 11:14
5. The area of the circle that can be inscribed in a square of side 8 cm is ____
(a) 36 π cm2.
(b) 16 π cm2.
(c) 12 π cm2.
(d) 9 π cm2
6. The area of the square that can be inscribed in a circle of radius 8 cm is ____
(a) 256 cm2
(b) 128 cm2
(c) 642 cm2
(d) 64 cm2
7. The area of a sector of a circle with radius 6 cm if the angle of the sector is 60° will be ___
(a) 142/7
(b) 152/7
(c) 132/7
(d) 122/7
8. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre.
The length of the arc is ____
(a) 20 cm
(b) 21 cm
(c) 22 cm
(d) 25 cm
9. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre.
The area of the sector formed by the arc is _____
(a) 200 cm2.
(b) 220 cm2.
(c) 231 cm2.
(d) 250 cm2.
10. Area of a sector of angle p (in degrees) of a circle with radius R is _____
(a) p/180 × 2πR
(b) p/180 × π R2
(c) p/360 × 2πR
(d) p/720 × 2π R2
11. Area of a circular region ___
(a) π r
(b) 2πr
(c)2π r2
(d) πr2
12. Area of sector of angle Θ _____
(a) Θ/360 x πr
(b) Θ/360 x 2πr
(c) Θ/360 x π r2
(d) Θ/180 x π r2
13. The area of sector of a circle with radius 78cm. and angle 60° is ___
(a) \frac { 77 }{ 3 }
(b) \frac { 67 }{ 3 }
(c) \frac { 65 }{ 3 }
(d) \frac { 74 }{ 3 }
14. The area of the quadrant of a circle whose circumference is cm will be ____ cm.
(a) 164
(b) 154
(c) 144
(d) 124
15. The interior of a circle along with its boundary is called the ____ region of the circle.
(a) Circular
(b) Inside
(c) External
(d) Internal
16. The total ____ around a circle is called as the circumference.
(a) Area
(b) Volume
(c) Path
(d) Internal side
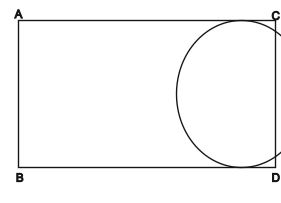
17. ABCD is a rectangle sheet of paper with AB = 40cm and BC = 14cm. A semi circle is cut as show. the area of the semi circle will be ____ cm
(a) 55 cm
(b) 65 cm
(c) 77 cm
(d) 108 cm
18. ABCD is a square from which another square AEOF is cut off the square ABCD has each side = 9 cm therefore the area of square AEOF will be ____( consider AE = 1/3 AD)
(a) 9 cm2
(b) 10 cm2
(c) 12 cm2
(d) 15 cm2
19. The perimeter of the sector with radius 10.5 cm and sector angle 60° is ____
(a) 32 cm
(b) 23 cm
(c) 41 cm
(d) 11 cm
20. In a circle of diameter 42 cm, if an arc subtends an angle of 60° at the centre, where π = 22/7 then length of arc is ____
(a) 11 cm
(b) 22/7 cm
(c) 22 cm
(d) 44 cm
21. The circumference of two concentric circles forming a ring are 88 cm and
66 cm. Taking π = 22/7, the width of the ring is _____
(a) 14 cm
(b) 7 cm
(c) 7/2 cm
(d) 21 cm
22. If the perimeter of a semicircular protractor is 72 cm where π = 22/7,
then the diameter of protractor is ____
(a) 14 cm
(b) 33 cm
(c) 28 cm
(d) 42 cm
23. If the radius of a circle is doubled, its area becomes ____
(a) 2 times
(b) 4 times
(c) 8 times
(d) 16 times
24. The perimeter of a circular and square fields are equal. If the area of the square field is 484 m² then the diameter of the circular field is ____
(a) 14 m
(b) 21 m
(c) 28 m
(d) 7 m
25. The area of the largest square that can be inscribed in a circle of radius 12 cm is ____
(a) 24 cm²
(b) 249 cm²
(c) 288 cm²
(d) 196√2 cm²
26. If the sum of the circumferences of two circles with radii R1 and R2 is equal to circumference of a circle of radius R, then ____
(a) R1 + R2 = R
(b) R1 + R2 > R
(c) R1 + R2 < R
(d) Can’t say.
27. The radius of sphere is r cm. It is divided into two equal parts. The whole surface area of two parts will be _____
(a) 8πr² cm²
(b) 6πr² cm²
(c) 4πr² cm²
(d) 3πr² cm²
28. If the diameter of a semicircular protractor is 14 cm, then its perimeter is ____ .
(a) 27 cm
(b) 36 cm
(c) 18 cm
(d) 9 cm
29. A race track is in the form of a circular ring whose outer and inner circumferences are 396 m and 352 m respectively. The width of the track is ____
(a) 63 m
(b) 56 m
(c) 7 m
(d) 3.5 m
30. The circumference of two concentric circles forming a ring are 88 cm and 66 cm. Taking π = 22/7, the width of the ring is _____
(a) 14 cm
(b) 7 cm
(c) 72 cm
(d) 21 cm
31. A steel wire when bent in the form of a square encloses an area of 121 cm². If the same wire is bent in the form of a circle, then the circumference of the circle is ____
(a) 88 cm
(b) 44 cm
(c) 22 cm
(d) 11 cm
32. The diameter of a circle whose area is equal to sum of the areas of the two circles of radii 40 cm and 9 cm is ____
(a) 41 cm
(b) 49 cm
(c) 82 cm
(d) 62 cm
33. The perimeter of a sector of radius 5.2 cm is 16.4 cm, the area of the sector is ____
(a) 31.2 cm²
(b) 15 cm²
(c) 15.6 cm²
(d) 16.6 cm²
34. If the radius of a circle is doubled, its circumference becomes ____
(a) 2 times
(b) 4 times
(c) 8 times
(d) 16 times
35. The area of the quadrant of a circle will be ___ of the total area of the circle
(a) 1/2 times
(b) 1/4 times
(c) 1/8 times
(d) 1/16 times
Answers. + Clues.
1 : (c) ⇒ The perimeter of the circle is equal to the circumference of the circle.
2 : (c)⇒ Radius = 5 cm and Area = πr2
3 : (a)⇒ The height of the largest triangle = radius of the semi-circle and
base = diameter of the semi-circle. Area of triangle = ½ x base x height
4 : (a)⇒ The perimeter of circle = perimeter of the square
2πr = 4a and Area of circle/Area of square
5 : (b) ⇒ Diameter of a circle = side of square = 8cm and Area of circle
6 : (b) ⇒ Diameter of circle = 16 cm = diagonal of the square
Let “a” be side, and hypotenuse = 16 cm. Use Pythagoras theorem
7 : (c) ⇒ Angle of the sector is 60° Area of sector = (θ/360°)×π r2
8 : (c) ⇒ Length of an arc = (θ/360°) × (2πr)∴ Length of an arc AB = (60°/360°) × 2 × 22/7 × 21
9 : (c) ⇒ angle subtended by arc = 60° , area of the sector = (60°/360°) × π r2 c
10 : (d) ⇒ The area of a sector = (θ/360°) × π r² and θ = p
So, area of sector = p/360 × π R2
11: (d) ⇒ Formula of area of circle
12: (c) ⇒ Formula of area of sector
13: (a) ⇒ Solve with area of sector formula
14: (b) ⇒ Use circumference = 2πr and find ‘r’ then put this value of r in 1/4 πr2
15: (a) ⇒ Definition of circular region
16: (b) ⇒ Definition of circumference of circle
17: (c) ⇒ D=2πr put this ‘r’ in 1/2 πr2 (since it is a semi circle)
18: (a) ⇒ Area of square is (side) 2
19 : (a) ⇒ Perimeter of sector = (θ/360 x2πr ) + 2r
20 : (c) ⇒Use length of arc formula
21 : (c) ⇒ Use circumference formula and find r1 and r2 then subtract the two radius
22 : (c) ⇒ Perimeter = πr + 2r formula and d = 2r
23 : (b) ⇒ Area =πr². If R= 2r then Area 4πr²
24 : (c) ⇒ From area of square we get r = 22cm and then use 2πr +2r
25 : (c) ⇒ Use Pythagoras thm and find one side of square , Then use area of square
26: (a) ⇒ Sum of the circumferences of two circles=circumference of a circle
27: (b) ⇒ Area of sphere = 4πr².It is divided by 2 = 2πr²Then 3 x 2πr²
28: (b) ⇒ Find radius and then perimeter
29: (c) ⇒ Find the two radius and subtract them
30: (c) ⇒ Find the two radius and subtract them
31: (b) ⇒ Area of square = Area of circle. Find radius. Put this in circumference formula
32: (c) ⇒ Add the two areas and equate it to the bigger area
33: (c) ⇒ From Perimeter formula get radius .Put this radius in Area formula
34: (b) ⇒ Instead of r put 2r in the formula and solve
35: (b) ⇒ Quadrant is one fourth part of a circle