ADDITIONAL QUESTIONS AND ANSWERS:

ADDITIONAL QUESTIONS AND ANSWERS:

1. A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. What is the total surface area of the combined solid?

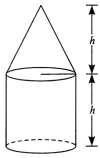
Ans: The total surface area of the combined solid in Fig.
= curved surface area of cone + curved surface area of cylinder + area of the base.

2.Two identical solid hemispheres of equal base radius r сm are struck together along their bases. What will be the total surface area of the combination?
Ans:  The resultant solid will be a sphere of radius r whose total surface area is 4πr².

3. A solid ball is exactly fitted inside the cubical box of side a. What is the volume of the ball?
Ans: Diameter of the solid ball = edge of the cube = a

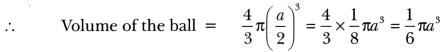
4. If two cubes of edge 5 cm each are joined end to end, find the surface area of the resulting cuboid.
Ans: Total length (l) = 5 + 5 = 10 cm
Breadth (b) = 5 cm, Height (h) = 5 cm
Surface Area = 2 (lb + bh + lh)
= 2(10 × 5 + 5 × 5 + 5 × 10)
= 2 × 125 = 250 cm²

5. A solid piece of iron in the form of a cuboid of dimension 49 cm × 33 cm × 24 cm is melted to form a solid sphere. Find the radius of sphere.
Ans: Volume of iron piece = Volume of the sphere formed
= 49 × 33 × 24 = 43 πr²

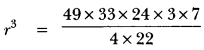
r = 21 cm

6. A mason constructs a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size 22.5 cm × 11.25 cm × 8.75 cm and it is assumed that space is covered by the mortar. Find the number of bricks used to construct the wall.
Ans:  Space occupied with bricks = 78 × volume of the wall
= 78 × 270 × 300 × 350

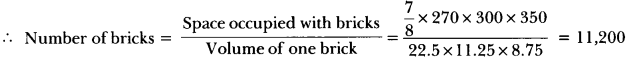
∴ The no: of bricks =11,200
7. The radii of the ends of a frustum of a cone 40 cm high are 20 cm and 11 cm. Find its slant height.
Ans:

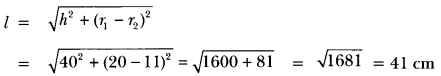
∴ The slant height is 41 cm
8. Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
Ans:  As per question
Volume of hemisphere = Surface area of hemisphere
= 2/3πr² = 3πr² 
∴ r = 9/2 units

9. A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes?
Ans: Volume of a cone: Volume of a hemisphere: Volume of a cylinder

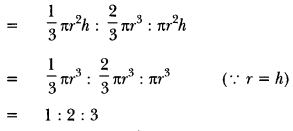
∴  the ratio of their volumes is 1 : 2 : 3

10. The slant height of the frustum of a cone is 5 cm. If the difference between the radii of its two circular ends is 4 cm, find the height of the frustum.
Ans: Let r and R be radii of the circular ends of the frustum of the cone.
Then, R – r = 4,   l = 5
We know, l² = (R – r)² + h²
⇒ 5² = 4² + h² or h² = 25 – 16 = 9
⇒ h = 3 cm

11. If the slant height of the frustum of a cone is 10 cm and the perimeters of its circular base are 18 cm and 28 cm respectively. What is the curved surface area of the frustum?
Ans: Let r and R be the radii of the two circular ends of the frustum of the cone.
Then, 2πr = 18 and 2πR = 28

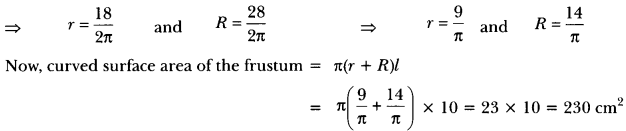
∴ the curved surface area of the frustum is 230 cm²

12. A vessel is in the form of a hollow hemisphere mounted by a hollow 7 cm cylinder. The diameter of the hemisphere is 14 cm and the total height T of the vessel is 13 cm. Find the inner surface area of the vessel.
Ans:

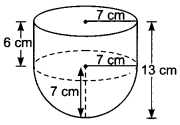
Here, radius of hemisphere =radius of cylinder = r cm = 7 cm
and height of cylinder, h = (13 – 7) cm = 6 cm
Now, inner surface area of the vessel
= Curved surface area of the cylindrical part + Curved surface area of hemispherical part = (2πrh + 2πr²) = 2πr (h + r)
= 2 × 22/7 × 7 (6 + 7)
= 2 × 22 × 13 = 572 cm²

13. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of T.
Ans:


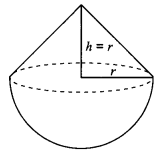
We have Height of cone is equal to its radius
 h = r = 1 cm (Given)
Also, radius of hemisphere = r = 1 cm
Now, Volume of the solid
= Volume of the cone + Volume of the hemisphere


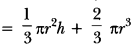
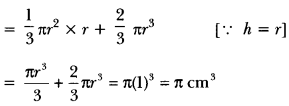
∴ the volume of the solid in terms of T is π cm³

14. If the total surface area of a solid hemisphere is 462 cm², find its volume. [Take π = 22/7]
Ans: Given, total surface area of solid hemisphere = 462 cm²
⇒ 3πr² = 462 cm²
3 × 22/7 × r² = 462
r² = 49 ⇒ r = 7 cm
Volume of solid hemisphere = 23 πr³
= 23 × 22/7 × 7 × 7 × 7
= 718.67 cm³

15. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Ans: The greatest diameter that a hemisphere can have = 7 cm = l
Radius of the hemisphere (R) = 72 cm
∴ Surface area of the solid after surmounting hemisphere
= 6l² – πR² + 2πR² = 6l² + πR²

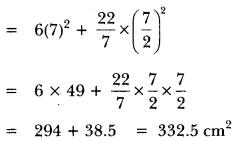
∴ the surface area of the solid is 332.5 cm²

16. The dimensions of a solid iron cuboid are 4.4 m × 2.6 m × 1.0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe.
Ans: Let the length of pipe by h m.
Volume of cuboid = 4.4 × 2.6 × 1 m²
Inner and outer radii of cylindrical pipe are 30 cm, (30 + 5) cm = 35 cm

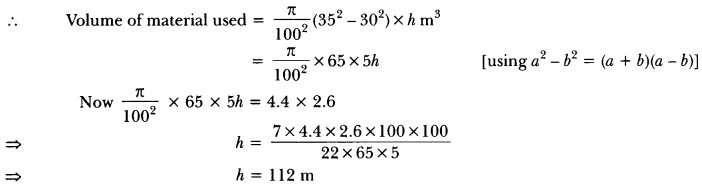
∴ the length of the pipe is 112 m

17. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius on its circular face. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Ans:

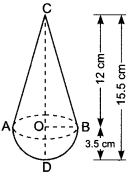
We have, CD = 15.5 cm and OB = OD = 3.5 cm
Let r be the radius of the base of cone and h be the height of conical part of the toy.
Then, r = OB = 3.5 cm
h = OC = CD – OD = (15.5 – 3.5) cm = 12 cm

∴ the total surface area of the toy is 214.5 cm².

18. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Ans: Here, we have
Edge of the cube = l = Diameter of the hemisphere
Therefore, radius of the hemisphere = l/2
∴ Surface area of the remaining solid after cutting out the hemispherical

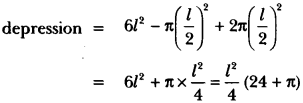
∴ the surface area of the remaining solid is l²/4 (24+ π)

19. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (Fig). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

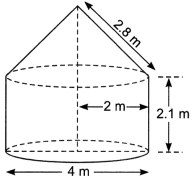
Ans:
Let the radius and height of the cylinder be r сm and h cm respectively. Then,

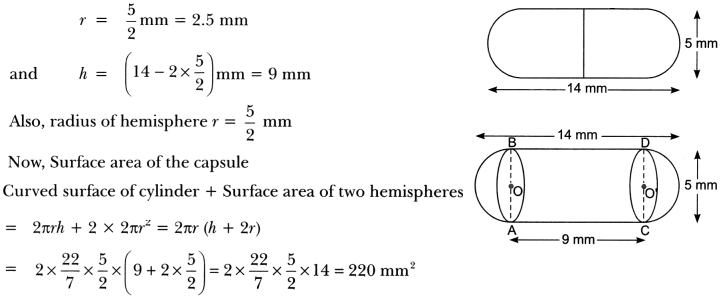
∴ its surface area is 220 mm²
20. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.

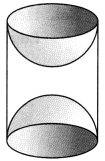
Ans: We have, r = 3.5 cm and h = 10 cm
Total surface area of the article
= Curved surface area of cylinder + 2 × Curved surface area of hemisphere
= 2πrh + 2 × 2πr² = 2πr (h + 2r)
= 2 × 227 × 3.5 × (10 + 2 × 3.5)
= 2 × 227 × 3.5 × 17 = 374 

Total surface area of the article= 374 
21. A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Ans: We have,
Radius of sphere (r₁) = 4.2 cm, Radius of cylinder (r₂) = 6 cm
Let h cm be the height of cylinder.
Now, since sphere is melted and recast into cylinder
∴ Volume of sphere = Volume of cylinder

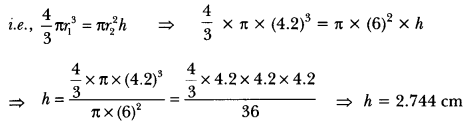
Hence, height of the cylinder is 2.744 cm.

22. What is the capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom?.
Ans:

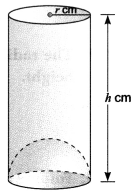
Capacity of the given vessel
= capacity of cylinder – capacity of hemisphere

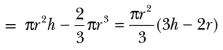
The capacity is π r /3 (5h −2r)

23. Two cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboid.
Ans:

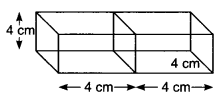
Let the length of each edge of the cube of volume 64 cm³ be x cm.
Then, Volume = 64 cm³
⇒ x² = 64
⇒ x² = 4³
⇒ x = 4 cm
The dimensions of cuboid so formed are
l = Length = (4 + 4) cm = 8 cm
b = Breadth = 4 cm and h = Height = 4 cm
∴ Surface area of the cuboid = 2 (lb + bh + lh)
= 2 (8 × 4 + 4 × 4 + 8 × 4)
= 2 (32 + 16 + 32)
= 160 cm²

24. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Ans:
The greatest diameter that a hemisphere can have = 7 cm = l
Radius of the hemisphere (R) = 72 cm
∴ Surface area of the solid after surmounting hemisphere
= 6l² – πR² + 2πR² = 6l² + πR²

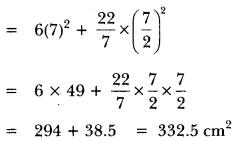
25. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Ans:
Here, we have
Edge of the cube = l = Diameter of the hemisphere
Therefore, radius of the hemisphere = l2
∴ Surface area of the remaining solid after cutting out the hemispherical

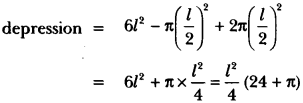
26. A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Ans:
Here, radius of cylindrical well =72m
Depth of cylindrical well = 20 m
Let H metre be the required height of the platform.
Now, the volume of the platform = Volume of the earth dugout from the cylindrical well

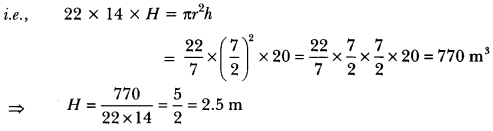
∴ Height of the platform = 2.5 m