ADDITIONAL QUESTIONS AND ANSWERS:

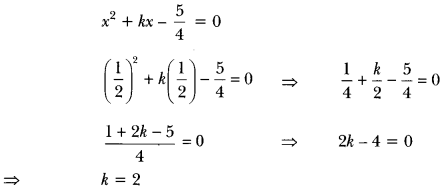
3) If ax² + bx + c = 0 has equal roots, find the value of c.
 Sol:  For equal roots D = 0
i.e., b² – 4ac = 0
⇒ b² = 4 ac
⇒ c = b² /4a
4) If a and b are the roots of the equation x² + Ax – B = 0, then find a and b.
 Sol:  Sum of the roots = a + b = – B/A = – a
Product of the roots = ab = B x A = – b
= a + b = – a and ab = −b
⇒ 2a = −b  and  a = −1
⇒ b = 2  and  a = −1

5) Show that x = – 2 is a solution  of  3x² + 13x + 14 = 0.
 Sol:  Put the value of x in the quadratic equation,
⇒ LHS = 3x² + 13x + 14
⇒ 3(−2)² + 13(−2) + 14
⇒ 12 – 26 + 14 = 0
⇒ RHS
Hence, x = −2 is a solution.

6) Find the discriminant of the quadratic equation 4√2x² + 8x + 2√2 = 0.
 Sol:  D = b² – 4ac
= (8)² – 4(4√2)(2√2)
⇒ 64 – 64 = 0

7) State whether the equation (x + 1)(x – 2) + x = 0 has two distinct
real roots or not. Justify your answer.
 Sol:  (x + 1)(x – 2) + x = 0
⇒ x² – x – 2 + x = 0
⇒ x² – 2 = 0
D = b² – 4ac
⇒ (−4)(1)(−2) = 8 > 0
∴ Given equation has two distinct real roots.

8) Is 0.3 a root of the equation x² – 0.9 = 0? Justify.
 Sol: Since  0.3 is a root of the equation x² – 0.9 = 0
∴ x² – 0.9 = (0.3)² – 0.9 = 0.09 – 0.9 ≠ 0
Hence, 0.3 is not a root of given equation.

9) For what value of k, is 3 a root of the equation 2x² + x + k = 0?
 Sol:  3 is a root of 2x² + x + k = 0, when
⇒ 2(3)² + 3 + k = 0
⇒ 18 + 3 + k = 0
⇒ k = – 21

10) Find the values of k for which the quadratic equation 9x² – 3kx + k = 0 has equal roots.
 Sol:  For equal roots: D = 0
⇒ b² – 4ac = 0
⇒ (− 3k)² – 4 × 9 × k = 0
⇒ 9k² = 36k
⇒ k = 4

11) Find the value of k for which the equation x² + k(2x + k – 1)+ 2 = 0 has real and equal roots.
 Sol: Given quadratic equation: x² + k(2x + k−1) + 2 = 0
= x² + 2kx + (k² – k + 2) = 0
For equal roots, b² – 4ac = 0
⇒ 4k² – 4k² + 4k – 8 = 0
⇒ 4k = 8
⇒ k = 2

12) If −5 is a root of the quadratic equation 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, then find the value of k.
 Sol:  Since – 5 is a root of the equation 2x² + px – 15 = 0
∴ 2 (−5)² + p (−5) – 15 = 0
⇒ 50 – 5p – 15 = 0    or    5p = 35    or   p = 7
Again p (x² + x) + k = 0   or   7x² + 7x + k = 0 has equal roots
∴ D = 0
i.e., b² – 4ac = 0   or   49− 4 × 7k = 0
⇒ k = 49/28 = 7/4

13) Does there exist a quadratic equation whose coefficients are rational but both of its roots are irrational? Justify your answer.
 Sol: Yes, x² – 4x + 1 = 0 is a quadratic equation with rational coefficients.

14) Write the set of values of k for which the quadratic equation 2x² + kx + 8 = 0 has real roots.
 Sol:  For real roots, D ≥ 0
⇒ b² – 4ac ≥ 0
⇒ k² – 4(2)(8) ≥ 0
⇒ k² – 64 ≥ 0
⇒ k²  ≥ 64
⇒ k ≤ −8   and   k ≥ 8

15) Solve the quadratic equation 2x² + ax – a² = 0  for  x.
 Sol:  2x² + ax – a² = 0
Here, a = 2,  b = a  and  c = −a².
Using the formula,

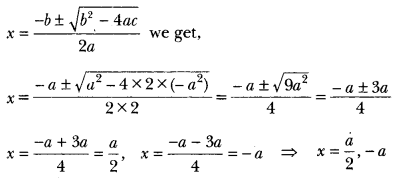
16) Find the roots of the quadratic equation
 Sol: The given quadratic equation is
√2x² + 7x + 5√2 = 0
By applying mid term splitting, we get
√2x² + 2x + 5x + 5√2 = 0
⇒ √2x (x + √2) + 5(x + √2)
⇒ (√2x + 5) + 5(x + √2) = 0
⇒ x = −5/√2   or  x = −5√2/5

17) Find the values of p for which the quadratic equation 4x² + px + 3 = 0 has equal roots.
 Sol: For equal roots;
D = 0
⇒ b² – 4ac = 0
⇒ p² – 4 × 4 × 3 = 0
⇒ p² – 48 = 0
⇒ p² = 48
⇒ p = ± √48
⇒ p = 4√3  or  −4√3

18) Solve for x: √3x² – 2√3x – 2√3 = 0
 Sol:  √3x² – 2√3x – 2√3 = 0
⇒ √3x² – 3√2x + √2x – 2√3 = 0
⇒ √3x (x – √6) + √2(x – √6) = 0
⇒ (√3x + 2) (x – √6) = 0
⇒ √3x + √2 = 0 or  x – √6 = 0
⇒ x = −√2√3  or  x = √6

19) If x = 23 and x = −3 are roots of the quadratic equation
ax² + 7x + b = 0, find the values of a and b.
 Sol:  Let us assume the quadratic equation be Ax² + Bx + C = 0.
Sum of the roots = –BA

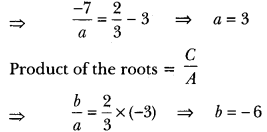
20) A two-digit number is four times the sum of the digits. It is also equal to 3 times the product of digits. Find the number.
 Sol: Let the ten’s digit be x and unit’s digit = y
Number 10x + y

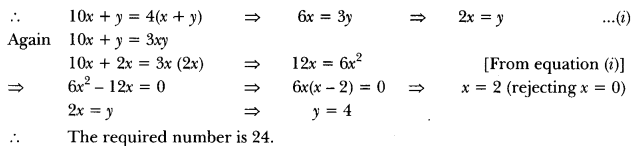
21) Find the value of p, for which one root of the quadratic equation
px² – 14x + 8 = 0 is 6 times the other.
 Sol:  Let the roots of the given equation be α and 6α.
Thus the quadratic equation is (x –α ) (x – 6α) = 0
⇒ x² – 7αx + 6α² = 0 …(i)
Given equation can be written as

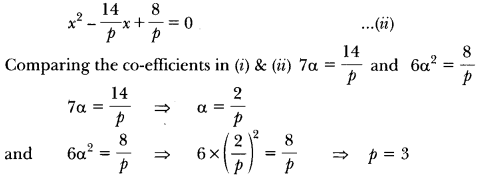
22) Find the roots of the following quadratic equations by factorisation:
(i) √2x² + 7x + 5√2 = 0    (ii) 2x² – x + 18 = 0
 Sol:  (i) We have, √2x² + 7x + 5√2 = 0
= √2x² + 5x + 2x + 5√2 = 0
⇒x (√2x + 5) + √2 (√2x + 5) = 0
⇒ (√2x + 5)(x + √2) = 0
∴ Either √2x + 5 = 0  or  x + √2 = 0
∴ x = – 5/√2  or   x = −√2
Hence, the roots are – 5/√2 and −√2.
(ii) We have, 2x² – x + 18 = 0

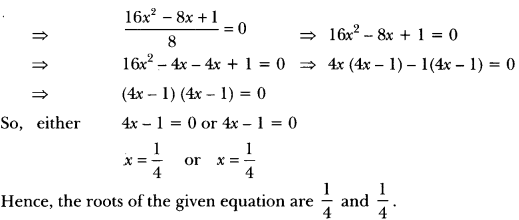
23) Find the roots of the following quadratic equations by applying the quadratic formula.
(i) 2x² – 7x + 3 = 0
(ii) 4x² + 4√3x + 3 = 0
 Sol: (i) We have, 2x² – 7x + 3 = 0
Here, a = 2,  b = −7  and  c = 3
Therefore, D = b² – 4ac
⇒ D = (−7)² – 4 × 2 × 3 = 49 – 24 = 25
∵ D > 0, ∴ roots exist.

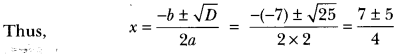
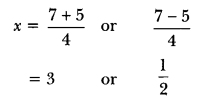
So, the roots of given equation are 3 and 1/2

(ii) We have, 4x² + 4√3x + 3 = 0
Here, a = 4,   b = 4√3  and  c = 3
Therefore, D = b² – 4ac = (4√3)² – 4 × 4 × 3 = 48 – 48 = 0
∴ D = 0, roots exist and are equal.

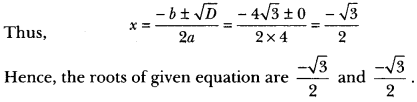
24) Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
(i) 3x² – 4√3x + 4 = 0    (ii) 2x² – 6x + 3 = 0
 Sol:  (i) We have, 3x² – 4√3x + 4 = 1
Here, a = 3,   b = – 4√3    and   c = 4
Therefore,  D = b² – 4ac
⇒ (− 4√3)² – 4 × 3 × 4
⇒ 48 – 48 = 0
Hence, the given quadratic equation has real and equal roots.

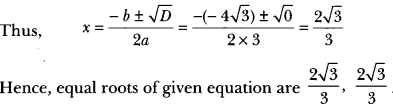
25) Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(i) 2x² + kx + 3 = 0
(ii) kx (x – 2) + 6 = 0
 Sol:  (i) We have, 2x² + kx + 3 = 0
Here, a = 2,   b = k,   c  = 3
D = b² – 4ac = k² – 4 × 2 × 3 = k² – 24
For equal roots  D = 0
i.e., k² – 24 = 0
⇒ ķ² = 24
⇒ k = ± √24
⇒ k = + 2√6

26) Determine the condition for one root of the quadratic equation
ax² + bx + c = 0 to be thrice the other.
 Sol: Let the roots of the given equation be a and 3α.

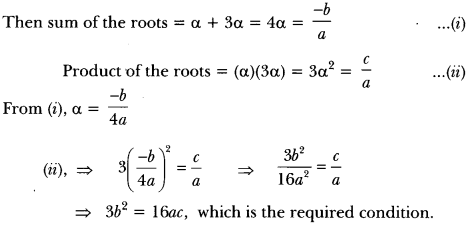
27) The sum of the reciprocals of Rashid’s age (in years) 3 years ago and 5 years from now is 1/3. Find his present age.
 Sol: Let the present age of Rashid be x years.
So, 3 years ago, Rashid’s age = (x – 3) years
And 5 years from now, Rashid’s age = (x + 5) years
Now, according to the question, we have

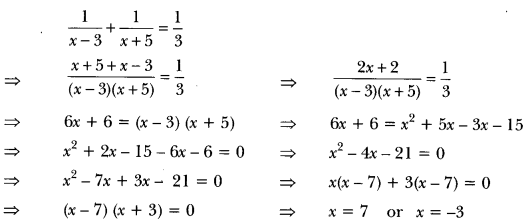
But x ≠ −3 (age cannot be negative)
Therefore, present age of Rehman = 7 years.

28) The difference of two natural numbers is 5 and the difference of their reciprocals is 110. Find the numbers.
 Sol: Let the two natural numbers be x and y such that x > y.
According to the question,
Difference of numbers, x – y = 5 ⇒ x = 5 + y …..(i)
Difference of the reciprocals,

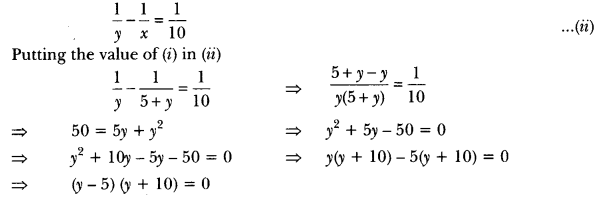
∴ y is a natural number.
∵ y = 5
Putting the value of y in (i), we have
⇒ x = 5 + 5
⇒ x = 10
29) The required numbers are 10 and 5.The sum of the squares of two consecutive odd numbers is 394. Find the numbers.
 Sol:  Let the two consecutive odd numbers be x and x + 2.

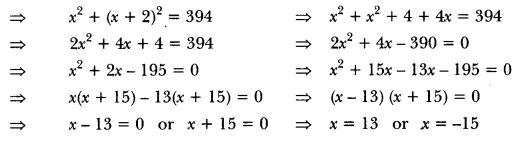
Hence, the numbers are 13 and 15  or  −15 and −13.

30) The sum of two numbers is 15 and the sum of their reciprocals is 3. Find the numbers.
 Sol:  Let the numbers be x and 15 – x.
According to given condition,

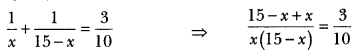
⇒ 150 = 3x (15 – x)
⇒ 50 = 15x – x²
⇒ x² – 15x + 50 = 0
⇒ x² – 5x – 10x + 50 = 0
⇒ x (x – 5) −10(x – 5) = 0
⇒ (x – 5) (x – 10) = 0
⇒ x = 5   or   10.
When x = 5,  then  15 – x = 15 – 5 = 10
When x = 10, then 15 – x = 15 – 10 = 5
Hence, the two numbers are 5 and 10.