ADDITIONAL QUESTIONS AND ANSWERS.
1) Which of the following can be the nth term of an AP?
4n + 3, 3n2 + 5, n2 + 1 . Give reason.
Sol: 4n + 3 because nth term of an AP can only be a linear relation in n like an = a + (n – 1) d.
2) Is 144 a term of the AP: 3, 7, 11, …? Justify your answer.
Sol: No, because here a = 3 is an odd number and d = 4 which is even. so, sum of odd and even must be odd whereas 144 is an even number.
3) The first term of an AP is p and its common difference is q. Find its 10th term.
Sol: a10 = a + 9d = p + 9q.
4) For what value of k: will 2k, k + 10 and 3k + 2 are in AP?
Sol: Given numbers are in AP
∴ (k + 10) – 2k = (3k + 2) – (k + 10)
⇒ −k + 10 = 2k – 8 ⇒ 3k = 18 ⇒ k = 6.
5) If an = 5 – 11n, find the common difference.
Sol: We have an = 5 – 11n
Let d be the common difference
d = an+1 – an
= 5 – 11(n + 1) – (5 – 11n)
= 5 – 11n – 11 −5 + 11n = −11
∴ d = − 11
6) For what value of p are 2p + 1, 13, 5p – 3, three consecutive terms of AP?
Sol: Since 2p + 1, 13, 5p – 3 are in AP.
∴ Second term – First term = Third term – Second term
⇒ 13 – (2p + 1) = 5p – 3 – 13
⇒ 13 – 2p – 1 = 5p – 16
⇒ 12 – 2p = 5p – 16
⇒ −7p = – 28
⇒ p = 4
7) In an AP, if d = −4, n = 7, a, = 4 then find a.
Sol: We know, an = a + (n – 1)d
Putting the values given, we get
⇒ 4 = a + (7 – 1)(−4) ⇒ a = 4 + 24
⇒ a = 28
8) Find the common difference of an AP in which a18 – a14 = 32.
Sol: Given, a18 – a14 = 32
⇒ (a + 17d) – (a + 13d) = 32
⇒ 17d – 13d = 32 ⇒ d = 324
9) If 7 times the 7th term of an AP is equal to 11 times its 11th term,
then find its 18th term.
Sol: Given, 7a7 = 11a11
⇒ 7 (a + 6d) = 11(a + 10d)
⇒ 7a + 42d = 11a + 110d
⇒ 4a + 68d = 0
⇒ a + 17d = 0
∴ a18 = a + 17d = 0
10) In an AP, if a = 1, an = 20, and Sn= 399, then find n.
Sol: Given, an = 20
= 1 + (n – 1)d = 20
⇒ (n – 1) d = 19
Sn= n/2 { 2a + (n – 1) d }
⇒ 399 = n/2 { 2 × 1 + 19 }
⇒ 399 × 2/21 = n
⇒ n = 38
11) Find the 9th term from the end (towards the first term) of the AP 5, 9, 13, …, 185.
Sol: l = 185, d = 4
l9 = l – (n – 1) d
= 185 – 8 × 4 = 153
Sol: We have, last term = 1 = 253
And, common difference d = 2nd term – 1st term = 8 – 3 = 5
Therefore, 20th term from end = 1 −(20 – 1) × d = 253 – 19 × 5
⇒ 253 – 95 = 158.
Sol: Let the first term be ‘a’ and common difference be ‘d’.
Given, a = 5, Tn = 45, Sn = 400 .
Tn = a + (m – 1) d
⇒ 45 = 5 + (m – 1) d
⇒ (n – 1) d = 40 ………(i)
Sn = n/2 (a + Tn)
⇒ 400 = n/2 (5 + 45)
⇒ n = 2 × 8 = 16 substituting the value of n in (i)
⇒ (16 – 1) d = 40
⇒ d = 40/15 = 8/3
Sol: Given: Sn = 3n2 +6n
Sn−1 = 3(n – 1)2 + 6(n – 1)
⇒ 3(n2 + 1 – 2n) + 6n – 6
⇒ 3n²+ 3 – 6n + 6n – 6 = 3n2 – 3
The nth term will be an
Sn = Sn−1 + an
an = Sn – Sn−1
⇒ 3n2 + 6n – 3n2 + 3
⇒ 6n + 3
15) What is the common difference of an AP in which a21 – a7 = 84?
Sol: Given: a21 – a7 = 84
⇒ (a + 20d) – (a + 6d) = 84
⇒ 14d = 84
⇒ d = 6
16) For what value of n, are the nth terms of two AP’s
63, 65, 67,… and 3, 10, 17,… equal?
Sol: Let nth term for two given series be an and a’n
According to the question
an = a’n
⇒ a + (n – 1) d = a + (n – 1) d’
⇒ 63 + (n – 1) 2 = 3 + (n – 1) 7
⇒ 5n = 65
⇒ n = 13.
17) Which term of the AP: 3, 8, 13, 18, … , is 78?
Sol: Let an be the required term and we have given AP
3, 8, 13, 18, …..
Here, a = 3, d = 8 – 3 = 5 and an = 78
Now, an = a + (n – 1) d
⇒ 78 = 3 + (n – 1) 5
⇒ 78 – 3 = (n – 1) × 5
⇒ 75 = (n – 1) × 5
⇒ 755 = n – 1
⇒ 15 = n – 1
⇒ n = 15 + 1 = 16
Hence, 16th term of given AP is 78.
18) Which term of the arithmetic progression 5, 15, 25, …. will be 130 more than its 31st term?
Sol: We have, a = 5 and d = 10
∴ a31 = a + 30d = 5 + 30 × 10 = 305
Let nth term of the given AP be 130 more than its 31st term. Then,
an = 130 + a31
∴ a + (n – 1) d = 130 + 305
⇒ 5 + 10(n – 1) = 435
⇒ 10(n – 1) = 430
⇒ n – 1 = 43
⇒ n = 44
Hence, 44th term of the given AP is 130 more than its 31st term.
19) In an AP: given l = 28, s = 144, and there are total 9 terms. Find a.
Sol: We have, l = 28, s = 144 and n = 9
Now, l = an = 28
28 = a + (n – 1) d 28 = a + (9 – 1)d
⇒ 28 = a + 8d ……(i)
and S = 144
⇒ 141 = 12 [2a + (n – 1) d]
⇒ 144 = 92 [12a +(9 – 1) d]
144 × 29 = 2a + 8d
⇒ 32 = 2a + 8d
⇒ 16 = a + 4d … (ii)
Now, subtracting equation (ii) from (i), we get
4d = 12 or d = 3
Putting the value of d in equation (i), we have
a + 8 × 3 = 28
⇒ a + 24 = 28
⇒ a = 28 – 24 =4
20) How many terms of the AP: 9, 17, 25, … must be taken to give a sum of 636?
Sol: Let sum of n terms be 636.
Sn = 636, a = 9, d = 17 – 9 = 8
⇒ n/2 [ 2a + (n – 1) d] = 636
⇒ n/2 [2 x 9 + (n – 1) × 8] = 636
⇒ n/2 × 2 [9+ (n – 1) 4] = 636
⇒ n [9 + 4n – 4] = 636
⇒ n [5 + 4n] = 636
⇒ 5n + 4n2 = 636
⇒ 4n2 + 5n – 636 = 0
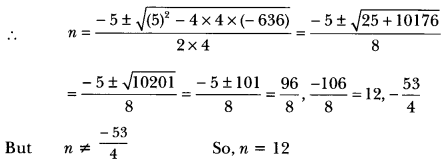
Thus, the sum of 12 terms of given AP is 636.
21) The first term, common difference and last term of an AP are 12, 6 and 252 respectively. Find the sum of all terms of this AP.
Sol: We have, a = 12, d = 6 and l = 252
Since, l = 252 ⇒ an = 252
= l = a + (n – 1) d
⇒ 252 = 12 + (n – 1) × 6
⇒ 240 = (n – 1) × 6
⇒ n – 1 = 40 or n = 41
Thus, Sn = n/2 (a + l)
⇒ S41 = 41/2 x (12 + 252) = 41/2 x (264)
= 41 × 132 = 5412
⇒ S41 = 5412
22) The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
Sol:
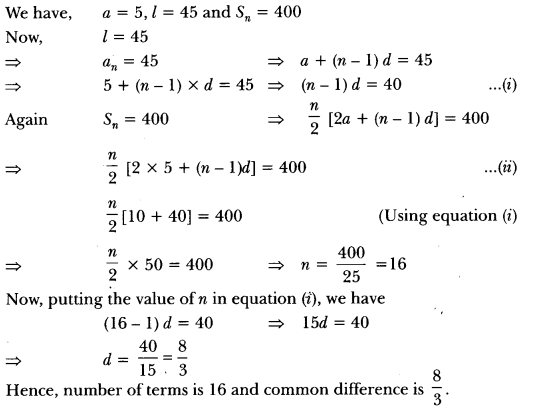
23) Find the sum of all two digit natural numbers which are divisible by 4.
Sol: Here a = 12, d = 4, an = 96
The formula is an = a + (n – 1) d
Therefore 96 = 12 + (n – 1) × 4
⇒ 96 = 8 + 4n
⇒ n = 88/4
⇒ n = 22
Apply the formula for sum,
⇒ Sn = n/2 [2a + (n – 1) d]
Hence, S22 = 11/24 + 21 × 4] = 11 [24 + 84]
= 11 × 108 = 1188.
24) If S, denotes the sum of the first n terms of an AP, prove that S30 = 3 (S20 – S10).
Sol: