Goa Board Paper OCTOBER 2014
1 (A) Select and write the most appropriate alternative from those provided in the bracket :
The H.C. F. and L.C.M of two numbers are 12 and 72 respectively. If one of the numbers is 24, then the other number is ____.
[ 4 , 36 , 84 , 144 ]
Ans : 36
(B) Attempt the following :
(i). Find the sum of the zeros of the quadratic polynomial 3x2 + 2x − 5.
Ans : Sum of the zeros = − \frac{b}{a} = − \frac{2}{3}
(ii). Determine whether is a zero of the quadratic polynomial x2 − 3.
Ans : Put x2 −3 = 0
x2 = 3
x = ± \sqrt{3}
\sqrt{3} is a zero of the polynomial
OR
Put x = \sqrt{3} in the given polynomial
Value of the polynomial = ( \sqrt{3})2− 3
= 3 − 3 = 0
\sqrt{3} is a zero of the polynomial
(C) On dividing (2x3 − x2 + 5x − 3) by a polynomial g (x), the quotient and remainder were ( 2x − 1) and ( 3x − 2 ) respectively. Find g (x).
Ans : Using the formula p(x) = q(x) x g(x) + r(x)
2x3− x2 + 5x − 3 = ( 2x − 1 ) g (x) + ( 3x − 2)
2x3− x2 + 5x − 3 − 3x + 2 = ( 2x − 1 ) g (x)
2x3−x 2 + 2x − 1 = ( 2x − 1 ) g (x)
g (x) = (2x3 − x2 + 2x − 1 ) ÷ (2x − 1)
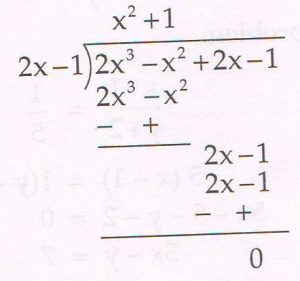
g (x) = x2 + 1
(D) Assuming that \sqrt{2} is an irrational number, prove that : 8 \sqrt{2} + 5 is an irrational number.
Ans : Let us assume, to the contrary , that 8 \sqrt{2} + 5 = \frac{a}{b}
8 \sqrt{2} = \frac{a}{b} − 5
8 \sqrt{2} = a − \frac{5b}{b}
\sqrt{2} = a − \frac{5b}{8b}
Now a and b are integers : a − 5b is an integer and 8b is an integer.
a − \frac{5b}{8b} is an rational number
This gives \sqrt{2} as a rational number
This leads to a contradiction as \sqrt{2} is irrational
Our assumption that 8 \sqrt{2} + 5 is rational, must be wrong.
8 \sqrt{2} + 5 is rational
2 (A) Select and write the most appropriate alternative from those provided in the bracket :
Five cards numbered as 1 , 2 , 3 , 4 , 5 are put in a box and mixed thoroughly. If a card is drawn at random from the box, then the probability that the number on the card is prime is ____.
[ \frac{1}{5} , \frac{2}{5} , \frac{3}{5} , \frac{4}{5} ]
Ans : \frac{3}{5}
(B) A die is thrown once. What is the probability that the number appearing on the top of the die is :
1. A perfect square?
Ans : All six possible outcomes are 1 , 2 , 3 , 4 5 and 6
Two favourable outcomes is 1 and 4
Probability that the outcome is a perfect square is \frac{2}{6}
= \frac{1}{3}
2. A multiple of 3 ?
Ans : There are six possible outcomes
Two favourable outcomes are 3 and 6
The probability that the outcome is a multiple of 3 is \frac{2}{6} = \frac{1}{3}
(C) Find the roots of ANY ONE of the following :
1. 3x2− 22x − 16 = 0
(By factorization method)
Ans : 3x2 − 22x − 16 = 0
3x2− 24x + 2x − 16 = 0
3x (x − 8 ) + 2 (x − 8 ) = 0
Either x − 8 = 0 OR 3x + 2 = 0
x = 8 OR x = − \frac{2}{3}
2. 2x2 + 13x − 24 = 0
(By quadratic formula )
Ans : 2x2 + 13x − 24 = 0
Here a = 2, b = 13 , c = − 24
D = b2 − 4ac
= (13)2− 4 × 2 ( − 24)
= 169 + 192
= 361
Roots are given by the formula
= − b ± \frac{ \sqrt{D} }{2a}
= − 13 ± \frac{ \sqrt{361} }{2 × 2}
= − 13 ± \frac{19}{4}
= − 13 + \frac{19}{4} and − 13 − \frac{19}{4}
= \frac{6}{4} and − \frac{32}{4}
= \frac{3}{2} and − 8
(D) Three consecutive positive integers are such that the sum of the square of the smallest number and the product of the other two is 46. Find the integers.
Ans : Let the 3 consecutive positive integers be x , x + 1 and x +2.
From the given condition,
x2 + ( x + 1 ) ( x + 2) = 46
x2 + x2 + x + 2x + 2 − 46 = 0
2x2 + 3x − 44 = 0
2x2 − 8x + 11x − 44 = 0
2x ( x − 4 ) + 11 (x − 4 ) = 0
( x − 4 ) ( 2x + 11 ) = 0
x − 4 = 0 or 2x + 11 = 0
x = 4 or x = − \frac{11}{2}
Since x is a positive integer − \frac{11}{2} is omitted.
x = 4
The 3 consecutive integer are 4 ,5 and 6
3(A) Select and write the most appropriate alternative from those provided in the bracket :
If the digit in the unit’s place of a two digit number is 2x and the digit in the ten’s place is y, then the two digit number is ____.
[ 2xy , 2x +y , 2x + 10y , 20x + y ]
Ans : 2x + 10y
(B) The following is a pair of linear equations:
− 2x + 3y = 6
4x − ky = 8
Answer the following questions with reference to the given pair of equations.
(1) Write the condition for a unique solution.
(2) Find the value of k.
Ans : (i) For a unique solution,
\frac{a1}{a2} ≠ \frac{b1}{b2}
− \frac{2}{4} ≠ \frac{3}{− k}
k ≠ 6
(ii). k has all values except 6
( C) Find the solution of ANY ONE of the following :
1. 7x − 3y = 11 ; 5x − 2y = 8
( By elimination method)
Ans : 7x − 3y = 11 … (1)
5x − 2y = 8 … (2)
Eq. (1) × 2, 14x − 6y = 22
Eq. (2) × 3, 15x − 6y = 24
− + −
______________
Subtracting − x = − 2
x = 2
Substituting x = 2 in eq (2),
We get 5 × 2 − 2y = 8
− 2y = 8 − 10
− 2y = −2
y = 1
The solution is x = 2 , y = 1
2. 7x − 2y = 3 ; 3x − y = 1
( By substitution method)
Ans : 7x − 2y = 3 … (1)
3x − y = 1 … (2)
Eq. (2) gives y = 3x − 1 … (3)
Substituting y in eq (1)
7x − 2 ( 3x − 1 ) = 3
7x − 6 + 2 − 3 = 0
x − 1 = 0
x = 1
Substituting x = 1 in Eq. (3), we get
y = 3 × 1 − 1
= 2
Solution is x = 1, y = 2
(D) A fraction reduces to \frac{1}{5} , if we subtract 1 from the numerator and add 2 to the denominator. It reduces to \frac{3}{3} ,if we only add 3 to the numerator. Find the fraction.
Ans : Let the fraction be \frac{x}{y} where y ≠ 0.
From the given condition,
\frac{( x −1)}{( y + 2)} = \frac{1}{5}
5 (x − 1 ) = 1 ( y + 2 )
5x − 5 − y − 2 = 0
5x − y = 7 … (1)
Also x + \frac{3}{y} = \frac{3}{4}
4x + 12 = 3y
4x − 3y = − 12 … (2)
Eq (1) × 3, 15 −3y = 21
− + −
_____________
− 11x = − 33
x = 3
Substituting x = 3 in Eq. (1),
5 × 3 − y = 7
15 − 7 = y
y = 8
The fraction is \frac{3}{8}
4 (A) Select and write the most appropriate alternative from those provided in the bracket :
The 20th term of the A.P. : 10 , 8 , 6 ,……. is _____.
[ − 180 , − 28 , 48 , 580 ]
Ans : − 28
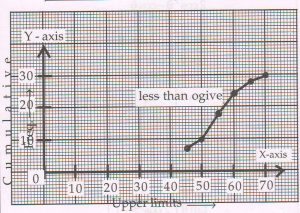
(B) The distribution given below, shows the weights of 30 students of a class:
|
Weight ( in kg) (Class – Interval) |
Number of students (Frequency) |
|
40 − 45 |
7 |
|
45 − 50 |
3 |
|
50 − 55 |
8 |
|
55 − 60 |
6 |
|
60 − 65 |
4 |
|
65 − 70 |
2 |
Prepare a cumulative frequency table of the less than type. Then taking a suitable scale, draw the ‘Less than type ogive’ on the graph paper provided.
Ans :
|
Weight ( in kg ) |
No. of students ( cumulative freq.) |
|
Less than 45 |
7 |
|
Less than 50 |
10 |
|
Less than 55 |
18 |
|
Less than 60 |
24 |
|
Less than 65 |
28 |
|
Less than 70 |
30 |
(C) The fourth term of an A.P is 17 and the sum of the third term and the seventh term is 42. Find the first term and the common difference.
Ans : Let the first term be ‘a’ and the common difference be ‘d’.
From the given condition,
a4 = 17
And a3 + a7 = 42
This gives a + ( 4 − 1) d = 17
a + 3d = 17 … (1)
And a + ( 3 −1 ) d + a + ( 7 − 1 ) d = 42
2a + 8d = 42
Dividing by 2,
We get a + 4d = 21 … (2)
a + 3d = 17 … (1)
− − −
_____________
d = 4
Subtituting d = 4 in Eq. (1)
a + 3 × 4 = 17
a = 17 − 12
a = 5
The first term is 5 and the common difference is 4.
(D) A life insurance agent found the following data of the distribution of the ages of 40 policyholders.
|
Age in years ( C.I ) |
No. of policy holders (fi ) |
Class mark (xi ) |
fi xi |
|
18 − 22 |
3 |
____ |
____ |
|
22 − 26 |
12 |
____ |
____ |
|
26 − 30 |
14 |
____ |
____ |
|
30 − 34 |
6 |
____ |
____ |
|
34 − 38 |
3 |
____ |
____ |
|
38 − 42 |
2 |
____ |
____ |
|
Total |
∑fi = 40 |
|
∑fi × xi = _ |
Rewrite and complete the table and hence find the mean age using the “Direct Method”.
Ans :
|
Age in years C.I
|
fi |
xi |
fixi |
|
18 − 22 |
3 |
20 |
60 |
|
22 − 26 |
12 |
24 |
288 |
|
26 − 30 |
14 |
28 |
492 |
|
30 − 34 |
6 |
32 |
192 |
|
34 − 38 |
3 |
36 |
108 |
|
38 − 42 |
2 |
40 |
80 |
|
Total |
∑fi= 40 |
|
∑fi xi =1120 |
Mean Age = \frac{∑fi × xi}{∑fi}
= \frac{1120}{40}
= 28 years
5 (A) Select and write the most appropriate alternative from those provided in the bracket :
If the diameter of a circle is 14 cm and the length of the tangent segment drawn from the external point P to the circle is 24 cm, then the distance of the point P from the centre of the circle is ___ cm.
[ 10 , 25 , 31 , 38 ]
Ans : 25
(B) In the given figure, two tangents Am and AN are drawn from an external point A to a circle with centre O touching the circle at M and N respectively
Prove that: AM = AN.
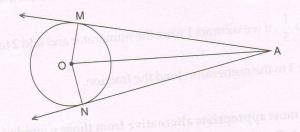
(Write only the proof with reasons)
Proof : Since tangent segments are perpendicular to the radii at the point of contact.
OM⊥ AM at M and ON ⊥ AN at N
In right Δs OMA and ONA
OA = OA ( common side )
OM = ON ( radii of the same circle )
ΔOMA ≅ ΔONA ( RHS congruency )
AM = AN ( c.p.c.t )
( C) Draw a circle with centre O and radius 3.8 cm. Take a point A in the exterior of the circle such that OA = 7.5 cm. Using a pair of compass and ruler, construct two tangents from point A to the circle touching it at P and Q respectively. Measure and state the length of the tangent segments.
Ans :
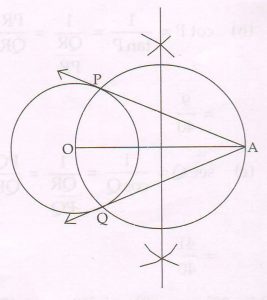
The length of each tangent segment is 6.3 cm
(D) Using a pair of compass and ruler construct ΔPQR with sides PQ = 7 cm, ∠ Q = 60° and QR = 5.5 cm. Then construct Δ P’QR’ whose sides are \frac{4}{5}of the corresponding sides of ΔPQR.
Ans :
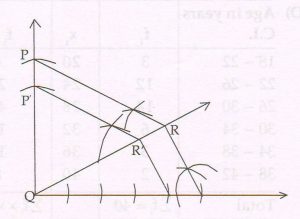
ΔP’QR’ is the required triangle whose sides are \frac{4}{5}of the corresponding sides of ΔPQR,
6 (A) Select and write the most appropriate alternative from those provided in the bracket :
If 1 + tan2 3A = sec2 42° where 3A is an acute angle, then the value of A = _____.
[ 14° , 16° , 42° , 126° ]
Ans : 14°
(B) Attempt ANY ONE of the following :
1. In ΔPQR, ∠R = 90°.
If cos P = \frac{9}{41} then find:
(a) The length of QR
(b) The value of cot P
(c) The value of sec Q
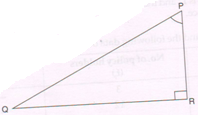
Ans : (a) cos P = \frac{PR}{PQ}
= \frac{9}{41}
Let PR = 9K and PQ = 41k, where k is a positive number
By Pythagoras theorem
QR2 = PQ2 − PR2
= ( 41k)2− ( 9k)²
= 1681k2− 81k2
= 1600k2
QR = \sqrt{1600k}²
= 40k
(b) cot P = \frac{1}{tanP} = \frac{1}{ \frac{QR}{PR} } = \frac{PR}{QR} = \frac{9K}{40K}
= \frac{9}{40}
(c) sec Q = \frac{1}{cosQ} = \frac{1}{ \frac{QR}{PQ} } = \frac{PQ}{QR} = \frac{41K}{40K}
= \frac{41}{40}
2. Evaluate the following using known values of trigonometric ratios:
Sec 30° × tan 60° − sin2 60° + cot 45°
Ans : Sec 30° tan 60° − sin2 60 + cot 45°
= \frac{2}{ \sqrt{3} } × \sqrt{3} − ( \frac{ \sqrt{3} }{2})² + 1
= 2 − \frac{3}{4} + 1
= 3 − \frac{3}{4}
= 12 − \frac{3}{4}
= \frac{9}{4}
= 2 \frac{1}{4}
(C ) Prove the following identity:
\frac{sin Ø − 2 sin³ Ø}{2 cos³ Ø − cos Ø} = tan Ø
Ans :
L.H.S. = \frac{sin Ø − 2 sin³ Ø}{2 cos³ Ø − cos Ø}
= \frac{sin Ø [ 1 − 2 sin² Ø] }{ cos Ø [ 2 cos² Ø - 1] }
= \frac{ tan Ø [ 1 − 2( 1 - cos² Ø) ]}{2 cos² Ø − 1}
= \frac{ tan Ø [ 1 − 2 + 2 cos² Ø ]}{2 cos² Ø − 1}
= \frac{ tan Ø [ 2 cos² Ø − 1 ]}{2 cos² Ø − 1}
= tan Ø = R.H.S.
(D) Attempt each of the following :
1. Find the distance between the points A ( − 3 , 0) and B ( − 5 , − 4).
Ans : AB2 = [ −3 −( −5)]2 + [ 0 − ( − 4)]2
= ( − 3 + 5)2 + ( 4)2
= (2)2 + 42
= 4 + 16
= 20
AB = \sqrt{20} =\sqrt{4} × 5 = 2 \sqrt{5} units
2. If P ( 2 , 6 ), Q ( − 4 ,2 ) and R (3 , − 2 ) are the vertices of Δ PQR, then find the area of ΔPQR.
Ans :
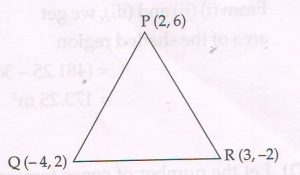
Area of ΔPQR
= \frac{1}{2} [ 2 (2 + 2) + ( − 4) ( − 2 − 2) + 3 (6 − 2) ]
= \frac{1}{2} [ 2 × 4 + ( − 4) ( − 4 ) + 3 × 4 ]
= \frac{1}{2} [ 8 + 16 + 12 ]
=\frac{1}{2} × 36
= 18 square units
7( A) Select and write the most appropriate alternative from those provided in the bracket :
If Δ WIN ∼ ΔFLY, ar( FLY) = 98 sq.cm and \frac{WN}{FY} = \frac{3}{7}, then ar (WIN) = ______ sq .cm.
[ 9 , 18 , 42 , 49 ]
Ans : 18
( B) Given : In ΔPQR, line l is drawn parallel to side QR to intersect side PQ at A and side PR at B respectively. BF ⊥side PQ.
Prove that: \frac{PA}{AQ} = \frac{PB}{BR}
(Write only the proof with reasons)
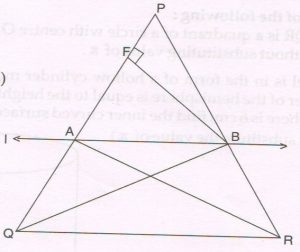
Proof : Let AE⊥ PB
Area of a triangle = \frac{1}{2} × base × height.
= ar ( PAB ) = \frac{1}{2} × PA × BF
= ar ( QAB ) = \frac{1}{2} × QA × BE
= ar ( PAB ) = \frac{1}{2} × PQ × AE
= ar ( RAB ) = \frac{1}{2} ×RB × AE
= \frac{ar ( PAB)}{ar ( QAB)} = \frac{ \frac{1}{2}× PA ×BF }{ \frac{1}{2} ×QA ×BF} = \frac{PA}{QA} … (1)
=\frac{ar ( PAB)}{ar ( RAB)} = \frac{ \frac{1}{2}× PB ×AE }{ \frac{1}{2} ×RB ×AE} = \frac{PB}{RB} … (2)
Now ΔQAB and ΔRAB are on the same base AB and between the same parallels QR and AD.
Ar( QAB) = ar ( RAB) … (3)
From (1), (2) and (3), we get
\frac{PA}{QA} =\frac{PB}{RB}
∴ \frac{PA}{AQ} =\frac{PB}{BR}
(C) Given : In right triangle, ABC , ∠B = 90°, D is the midpoint of side BC and DE⊥ side AC.
Prove that:
AB2 = AC. (AE − EC )
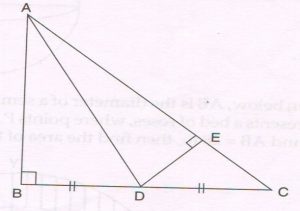
Proof: L.H.S = AB2
= AD2 − BD2 ( Pythagoras theorem to ΔABD)
= (AE2 + DE2 ) − DC2 ( Pythagoras theorem in ΔAED and using BD = DC)
= AE2 + DE2 − ( DE2 + EC2 ) (Pythagoras theorem in Δ DEC )
= AE2 + DE² − DE² − EC2
= AE2 − EC2
= ( AE + EC ) ( AE − EC )
= AC. ( AE − EC) (AC = AE + EC )
= R. H. S.
(D) A boy on top of a building AB, 12m high observes two parked cars P and Q at angles of depression 30° and 60° respectively. If the two cars and the foot ‘B’ of the building are in the same horizontal line as shown in the figure, find the distance between the two cars.
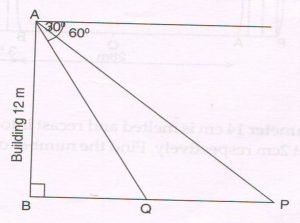
Ans : To find distance PQ
Let PQ = x meters and BP = y meters
BQ = ( y − x) meters
Now ∠ AQB = 60° and ∠ APB = 30°
In right Δ ABQ, tan 60°
= \frac{AB}{BQ} \sqrt{3}
\frac{12}{y − x} … (1)
In right ΔABP, tan 30°
=\frac{AB}{BP} \sqrt{3}
= \frac{12}{y } … (2)
∴ y = 12 \sqrt{3}
Substituting in (1), we get
\sqrt{3}
= \frac{12}{12 \sqrt{3}- x } \sqrt{3} ( 12 \sqrt{3} − x ) = 12
36 − x \sqrt{3} = 12
x \sqrt{3} = 36 − 12
x \sqrt{3} = 24
x = \frac{24}{ \sqrt{3} }
= \frac{24}{ \sqrt{3} } × \frac{ \sqrt{3} }{ \sqrt{3} }
= 24 \frac{ \sqrt{3} }{3}
PQ = 8 \sqrt{3} meters
Distance between the cars is 8 \sqrt{3} meters
8 (A) Select and write the most appropriate alternative from those provided in the bracket :
1. If the circumference and the area of a circle are numerically equal, then the radius of the circle is ____ units.
( π , 2 , 1 , 2π )
Ans : 2
2. The area of one face of a cube is 49 cm2, then the volume of the cube is ____ cm3.
[ 49 , 7 , 216 , 343 ]
Ans : 343
(B) Attempt each of the following :
1. If O − PQR is a quadrant of a circle with centre O and radius 4cm , then find the length of arc PQR without substituting value of π.
Ans : Length of arc PQR = \frac{Ø}{360 } × 2 π
= \frac{90}{360 } × 2 π × 4 cm
= 2 π cm
2. A vessel is in the form of a hollow cylinder mounted on a hollow hemisphere. The inner diameter of the hemisphere is equal to the height of the cylinder. If the inner diameter of the hemisphere is 6 cm, find the inner curved surface area of the cylinder.
(Do not substitute the value of π)
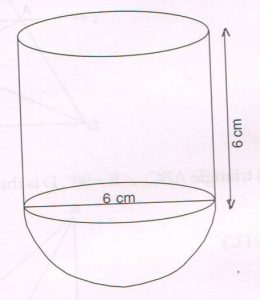
Ans : Inner curved surface area of the cylinder
= π r2h
= π × 3 × 3 × 6 cm2
= 54 π cm2
(c) In the figure given below, AB is the diameter of a semicircle lawn AXB. The shaded region which is a half ring, represents a bed of roses, where points P , Y, Q lie on the outer semicircle. If the width of the ring is 3.5 m and AB = 28 m , then find the area of the shaded region.
( Take π = \frac{22}{7 } )
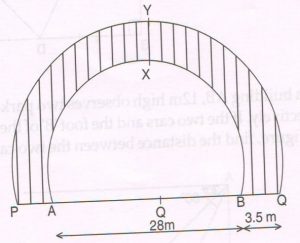
Ans : Area of the shaded region = area of outer semicircle – area of inner semicircle … (1)
= \frac{1}{2 } × π r2
= \frac{1}{2 } × \frac{22}{7 } × 14 × 14 m2
= 308 m2 … (2)
Area of the outer semicircle
= \frac{1}{2 } × π R2
= \frac{1}{2 } × \frac{22}{7 } × 17.5 × 17.5 m2
= 481.25 m2 …. (3)
From (1) (2) and (3), we get
Area of the shaded region
= ( 481.25 − 308 ) m2
= 173.25 m2
(D) A solid metallic sphere of diameter 14 cm is melted and recast into solid right circular cones each of base radius 3.5 cm and height 2 cm respectively. Find the number of cones formed.
( Take π = \frac{22}{7} )
Ans : Let the number of cones formed be N
Volume of the solid metallic sphere
= \frac{4}{3 } π R3
= \frac{4}{3 } × \frac{22}{7} × 7 × 7 × 7 cm3
= 88 × \frac{49}{3 } cm3 …. (1)
Volume of each solid right circular cone
= \frac{1}{3 } × π r2 h
= \frac{1}{3 } × \frac{22}{7} × 3.5 × 3.5 × 2
= 22 × 3.5 × \frac{1} {3} cm2 …. (2)
Number of cones, N
= \frac{88 × \frac{49}{3} }{22 ×\frac{3.5}{3} }
= \frac{88 \times 49}{22 \times 3.5}
= 4 × 7 × 7 × \frac{10} {35}
= 56
The number of cones is 56.