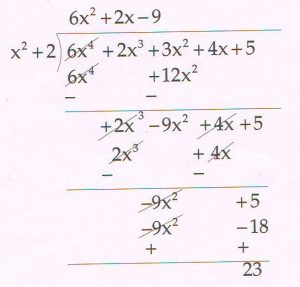Sample Papers Goa Board MARCH 2016
1 (A) Select and write the most appropriate alternative from those provided in the bracket :
The product of two numbers is 192. If their HCF is 8, then their LCM is _____.
[ 24 , 26 , 30 , 60 ]
Ans : 24
(B) Attempt the following :
1. Find the product of the zeros of the polynomial P (x) = 2x2 − 3x + 8
Ans : P (x) = 2x2 − 3x + 8
Product of the zeros = \frac{c}{a} = \frac{8}{2} = 4
2. Find the zeros of the polynomial 5x2 − 20.
Ans : Let P (x) = 5x2 − 20
= 5 (x2 − 4)
Zeros are given by x2 − 4 = 0
(x − 2) ( x+ 2) = 0
x − 2 = 0 OR x + 2 = 0
x = 2 OR x = − 2
Zeros are 2 and − 2
(C) Divide the polynomial 6x4 + 2x3 + 3x2 + 4x + 5 by x2 + 2 and write the quotient and remainder. Hence express your result in the form:
Dividend = Divisor × Quotient + Remainder.
Ans :
Quotient is 6x2 + 2x − 9
Remainder is 23
∴Dividend = Divisor × Quotient + Remainder. will be
6x4 + 2x3 + 3x2 + 4x + 5 = ( x2 + 2) ( 6x2 + 2x − 9 ) + 23
(D) Prove that: \sqrt{5} is an irrational number.
Proof:
Let us assume, to the contrary, that \sqrt{5} is rational
We can find integers a and b ( where b ≠ 0 )
Such that \sqrt{5} = \frac{a}{b}
Where a and b are coprime
b \sqrt{5} = a
5b2 = a2 …. (1)
a2 is divisible by 5
a is divisible by 5 ( using theorem ) …. (2)
a = 5c
For some integer c …. (3)
Substituting (3) in (1), we get
5b2 = 25 c2
b2 = 5 c2
b2 is divisible by 5
b is divisible by 5 …. (4)
From (2) and (4), a and b have 5 as a common factor.
This contradicts that a and b are coprime.
\sqrt{5} is rational is a wrong assumption
\sqrt{5} must be irrational.
2 (A) Select and write the most appropriate alternative from those provided in the bracket :
An unbiased die is thrown once, then the probability of getting an odd number on the top face of the die is ____.
( \frac{1}{6} , \frac{2}{3} , \frac{1}{2} , \frac{1}{3} )
Ans : \frac{1}{2}
(B) A box contains 40 discs which are numbered from 1 to 40 and mixed thoroughly. If one disc is drawn at random from the box, find the probability that the disc is drawn is :
1. A perfect square number
Ans : Number of all possible outcomes = 40
Let E be the event getting a perfect square number ( like 1 , 4 , 9 , 16 , 25 , 36 )
Outcomes favourable to E = 6
P ( a perfect square no.) = \frac{6}{40} = \frac{3}{20}
2. A number divisible by 5.
Ans : Let F be the event getting a number divisible by 5 ( like 5 , 10 , 15 , 20 , 25 , 30 , 35 , 40)
Outcome favourable to F = 8
P ( a number divisible by 5 ) = \frac{8}{40} = \frac{1}{5}
(C) Find the roots of ANY ONE of the following quadratic equations :
1. 4x2 − 11x + 6 = 0
( By factorization method )
Ans : 4x2 − 11x + 6 = 0
4x2 − 8x − 3x + 6 = 0
4x ( x − 2) ( 4x − 3) = 0
( x − 2) ( 4x − 3) = 0
Either x − 2 = 0 or 4x − 3 = 0
Either x = 2 or x = \frac{3}{4}
The roots of the equation are 2 and \frac{3}{4}
2. 3x2 − 4x − 7 = 0
( By using quadratic formula )
Ans : 3x2 − 4x − 7 = 0
Here a = 3, b = − 4 and c = − 7
Roots of the equation are given by
x = \frac{- b ± \sqrt{b² − 4ac} }{2a}
= − (− 4) ± \sqrt{16 − 4 × 3 × (− 7 )} 2 × 3
= 4 ± \frac{ \sqrt{16 + 84} }{6}
= 4 ± \frac{ \sqrt{100} }{6}
= 4 ± \frac{10}{6}
= x = 4 + \frac{10}{6} OR x = 4 − \frac{10}{6}
= x = \frac{14}{6} OR x = − \frac{6}{6}
= x = \frac{7}{3} OR x = − 1
Roots are − 1 and \frac{7}{3}
(D) A takes 10 days less than the time taken by B to finish an embroidery work. If both A and B together can finish the work in 12 days, find the time taken by B alone to finish the work.
Ans : Let the time taken by B to finish the work alone be x days
Then A alone will take x − 10 days
In 1 day, B finishes \frac{1}{x}of the work
And A finishes \frac{1}{x} − 10 of the work
Both together, in 1 day, finish ( \frac{1}{x} + \frac{1}{x − 10} ) of the work, which is \frac{1}{12} of the work
\frac{1}{x} + \frac{1}{x − 10} = \frac{1}{12}
12 ( x − 10 ) + 12x = x ( x − 10 )
12x − 120 + 12x = x2 − 10x
− x2 + 10x + 24x − 120 = 0
x2 − 34x + 120 = 0
( x − 30) ( x − 4) = 0
x = 30 or x = 4
According to the problem x = 4 is not possible
B alone can finish the work in 30 days and A alone will finish the work in 30 − 10 = 20 days
3 (A) Select and write the most appropriate alternative from those provided in the bracket :
If 11x + 3y = 28 and 3x + 11y = 14 then x + y = _____.
( 1 , 3 , 14 , 28 )
Ans : 3
(B) The cost of a pen is thrice the cost of a pencil. Also, 2 pens and 3 pencils together cost Rs 45. Represent the above statements by two linear equations in two variables.
Ans : Let the cost of a pen be Rs x
And the cost of a pencil be Rs y
1st eq. is x = 3y
Or x − 3y = 0 …. (1)
2nd eq. is 2x + 3y = 45 …. (2)
(C) Find the solution of ANY ONE of the following pairs of linear equations :
1. 7x + 5y = 12 and 4x + 3y = 9
( By elimination method )
Ans : 7x + 5y = 12 …. (1)
4x + 3y = 9 …. (2)
3 × eq (1) 21x + 15y = 36
5 × eq (2) 20x + 15y = 45
− − −
____________________
x = − 9
Substituting x = − 9 in eq (1),
We get 7 ( − 9) + 5y = 12
5y = 12 + 63
5y = 75
y = 15
The solution is x = − 9 , y = 15
2. 2x + 5y = 1 and 5x − 3y = 18
( By cross multiplication method )
Ans : 2x + 5y − 1 = 0
5x − 3y − 18 = 0
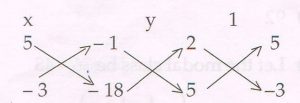
Then
\frac{x}{5 (− 18) − ( − 1)( − 3)}
= \frac{y}{5 (− 1)− 2 (− 18)}
= \frac{1}{2 (−3) − 5 × 5} \frac{x}{− 90 − 3}
= \frac{y}{− 5 +36}
= \frac{1}{− 6 − 25} \frac{x}{− 93}
= \frac{y}{31}
= \frac{1}{−31}
x = \frac{− 93}{− 31} = 3
y = \frac{31}{− 31} = − 1
Solution is x = 3 , y = − 1
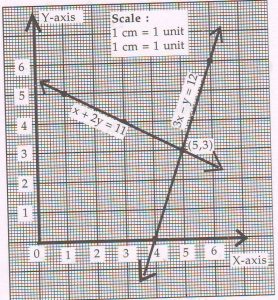
( D) Find the solution of the following pair of linear equations graphically :
3x − y = 12 and x + 2y = 11
Rewrite and complete the following tables.
3x − y = 12
|
x |
|
|
|
|
y |
|
|
|
x + 2y = 11
|
x |
|
|
|
|
y |
|
|
|
( Plot at least three points for each line using graph paper. )
Ans : 3x − y = 12
|
x |
4 |
5 |
6 |
|
y |
0 |
3 |
6 |
x + 2y = 11
|
x |
1 |
3 |
5 |
|
y |
5 |
4 |
3 |
Graphical solution is x = 5 , y = 3
4 (A) Select and write the most appropriate alternative from those provided in the bracket :
The 20th term of the Arithmetic Progression ; 16 , 20 , 24 , 28 …… is ____.
[ 60 , 84 , 92 , 108 ]
Ans : 92
(B) The marks distributed of 102 students in a mathematics test are as given below in the table :
|
Marks |
Number of shops |
|
0 − 12 |
22 |
|
12 − 24 |
10 |
|
24 − 36 |
25 |
|
36 − 48 |
30 |
|
48 − 60 |
15 |
Find the mode of this data.
Ans: Let the modal class be 36 − 48
Mode = l + ( \frac{ f_{1 }- f_{0} }{2 f_{1} - f_{0} - f_{2} } ) × h
Where
l = lower limit of the modal class = 36
f1 = frequency of the modal class = 30
f0 = frequency of the class preceding the modal class = 25
f2 = frequency of the class succeeding the modal class = 15
Mode = 36 + ( 30 − \frac{25}{2} × 30 − 25 − 15) × 12
= 36 + ( \frac{5}{20} ) × 12
= 36 + 3
Mode = 39
(C) Mr. X from his daily income makes some savings per day. In each month he saves Rs 250 on the 1st day, Rs 275 on the 2nd day, Rs 300, on the 3rd day and so on. Calculate the amount he saved for the month of February 2015.
Ans : Total amount Mr X saved in February 2015 is given by
S = \frac{n}{2} [ 2a + (n − 1) d ]
Where n = 28 days, a = Rs 250, d = 275 − 250 = Rs 25
S = \frac{28}{2} [ 2 × 250 + ( 28 − 1 ) 25 ]
= 14 [ 500 + 675 ]
= 14 × 1175
= 16,450
The amount saved by Mr. X is Rs 16,450
(D) The following table gives the daily income of 80 workers in a locality:
Taking class mark ( denoted by a ) of the class interval ( 90 − 120 ) as the Assumed Mean, rewrite and complete the table, and also find the mean of daily income by the ‘assumed mean’ method.
Ans :
Mean of daily income = a + \frac{∑fidi}{∑fi}
= 105 + \frac{− 360}{80}
= 105 − 4.5
= Rs 100.50
5 (A) Select and write the most appropriate alternative from those provided in the bracket :
Point P is at a distance of 41 cm from the center O, of a circle having a radius of 9 cm. Therefore the length of the tangent segment from point P to the circle is ____ cm
[ 4 , 32 , 40 , 50 ]
Ans : 40
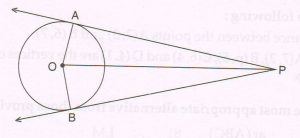
(B) Given : O is the center of the circle. Two tangent segments PA and PB are drawn from point P to the circle at A and B respectively.
Prove that: PA = PB.
Proof:
The tangent segments drawn from an external point to a circle are at right angles to the radii at the point of contact
∠OAP = ∠OBP = 90°
In right Δs OAP and BOP
OP = OP ( common side)
OA = OB ( radii of the same circle a)
Δ OAP ≅ ΔOBP ( Hypotenuse – side theorem)
PA = PB ( c.p.c.t )
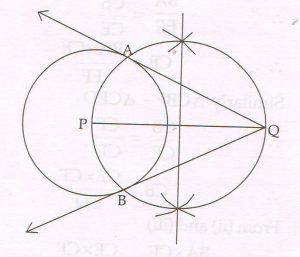
( C) Draw a line segment PQ of length 7.7 cm. Taking P as the center and radius 3.5 cm, draw a circle. Using a pair of compass and ruler, construct two tangents QA and QB to the circle from point Q. Measure and state the length of the tangent segments.
Ans :
The length of each tangent segment is 6.9 cm
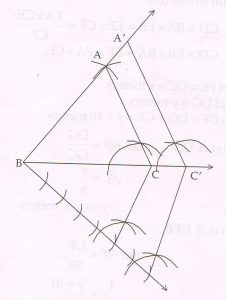
(D) Construct Δ ABC in which AB = 6.5 cm, BC = 7.5 cm and AC = 5.8 cm. using a pair of compass and ruler construct Δ A’BC’ similar to ΔABC whose sides are 7/5 of the corresponding sides of Δ ABC.
Ans :
ΔA’BC’ is the required triangle.
6 (A) Select and write the most appropriate alternative from those provided in the bracket :
If cosec 18° = sec 2A, then ∠ A = ____.
[ 18° , 36° , 72° , 162° ]
Ans : 36°
(B) Attempt ANY ONE of the following :
In ΔPQR, ∠Q = 90° and cos P = \frac{15}{17}, find:
(a) Length of QR
(b) Value of cot P
(c) Value of sin R
Ans :
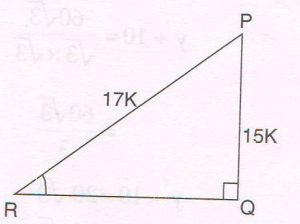
(a) cos P = \frac{15}{17}
Let PQ = 15k and PR = 17k
By Pythagoras theorem
RQ2 + PQ2 = PR2
RQ2 +( 15k )2 = ( 17k)2
RQ2 = 289k2 − 225k2
= 64k2
Length of RQ = 8k
(b) cot P = \frac{PQ}{RQ} = \frac{15k}{8k} = \frac{15}{8}
(c) sin R = \frac{PQ}{PR}= \frac{15k}{17k}= \frac{15}{17}
2. Evaluate the following expression using known numerical values :
12 sin2 60° − 8 sec2 45° + 3 tan2 30°.
Ans : 12 sin2 60° − 8 sec2 45° + 3 tan2 30°
= 12 × ( \frac{ \sqrt{3} }{2} )2 − 8 × ( \sqrt{2} )2 + 3 ( 1/ )2
= 12 × \frac{3}{4} − 8 × 2 + 3 × \frac{1}{3}
= 9 − 16 + 1
= − 6
( C) Prove the following identity :
( 1 + cot A − cosec A ) ( 1 + tan A + sec A ) = 2
Ans : L.H.S. = (1 + cot A − cosecA) ( 1 + tan A + sec A )
= \big(1 + \frac{cosA }{sin A}- 1 + \frac{1}{sinA} \big) \big(1 + \frac{sinA }{cos A} + 1 + \frac{1}{cos A} \big)
= \big( \frac{sinA + cos A- 1}{sinA} \big) \big( \frac{cos A + sin A + 1}{cos A} \big)
= \frac{(sin A + cos A)² − ( 1)²}{sin A cos A}
= \frac{sin² A+ cos² A + 2 sin A cos A − 1}{sin A cos A}
= \frac{1 + 2 sin A cos A − 1}{sinA cos A}
= \frac{2 sin A cos A}{sinA cos A}
= 2 = R.H.S.
(D) Attempt each of the following :
1. Find the distance between points A ( 2, 3 ) and B ( 6, 7 ).
Ans : \sqrt{(2 - 6)² + (3-7)²}
= \sqrt{( −4)² + (− 4)²}
= \sqrt{16 + 16}
= \sqrt{32}
= 4 \sqrt{2} units
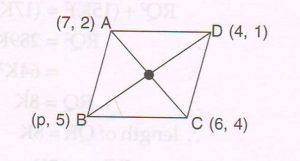
2. If the points A ( 7, 2 ) , B ( p , 5 ), C ( 6, 4 ) and D (4, 1 ) are the vertices of the parallelogram ABCD , find the value of p.
Ans :
In a parallelogram the diagonals bisect each other
Midpoint of AC = midpoint of BD
( 7 + \frac{6}{2} , 2 + \frac{4}{2} ) = ( p + \frac{4}{2} , 5 + \frac{1}{2} )
p + \frac{4}{2}
= 7 + \frac{6}{2}
p = 13 − 4 = 9
7 (A) Select and the most appropriate alternative from those provided in the bracket :
If ΔABC ∼ ΔLMN and \frac{ar (ABC)}{ar (LMN)} = \frac{8}{100} , then \frac{LM}{AB} = ____.
( \frac{10000}{6481} , \frac{6481}{1000} , \frac{9}{10} , \frac{10}{9} )
Ans : \frac{10}{9}
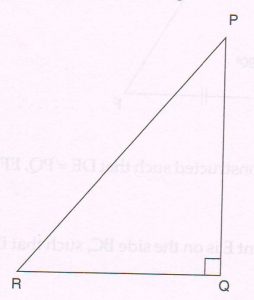
(B) With reference to the given figure and given condition, write only the proof with reasons of the following theorem.
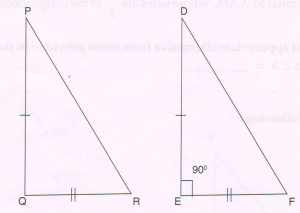
Given : In ΔPQR, PQ2 + QR2 = PR2, ΔDEF is constructed such that DE = PQ, EF = QR and ∠E = 90°.
Prove that : ΔPQR is a right angled triangle.
Proof: In right ΔDEF, by Pythagoras theorem
DF2 = DE2 + EF2
DF2 = PQ2 + QR2 ( using given condition)
Now PR2 = PQ2 + QR2 ( using given condition )
DF2 = PR2
DF = PR …. (1)
Now in ΔDEF and ΔPQR,
DF = PR [proved in (1)]
DE = PQ ( given )
EF = QR ( given)
Δ DEF ≅ Δ PQR ( by SSS congruency)
∠E = ∠Q ( c.p.c.t )
But ∠E = 90°
ΔPQR is a right angled triangle.
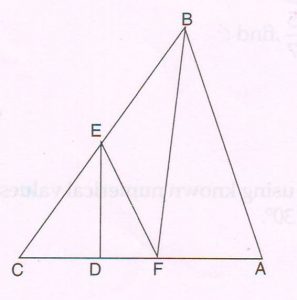
(C) In ΔABC, D and F are on the side CA and point E is on the side BC, such that DE \| FB and FE \| AB , as shown in the figure.
Prove that : CD × EB × BA = EF × FA × CE
Proof: In Δ CBA, since EF \| BA, by basic proportionality theorem
\frac{CF}{FA} = \frac{CE}{EB}
EB = FA × \frac{CE}{CF} …. (1)
Now ΔCBA ∼ ΔCEF ( by AA proportionality theorem)
\frac{BA}{EF} = \frac{CB}{CE}
CB = BA × \frac{CE}{EF} …. (2)
Similarly ΔCBF ∼ ΔCED
\frac{CB}{CE}= \frac{CF}{CD}
CB = CE × \frac{CF}{CD} …. (3)
From (2) and (3)
BA × \frac{CE}{EF} = CE × \frac{CF}{CD}
CD × BA = EF × CF …. (4)
Multiply (1) and (4)
CD × BA × EB = EF × CF × FA × \frac{CE}{CF}
CD × EB × BA = EF × FA × CE.
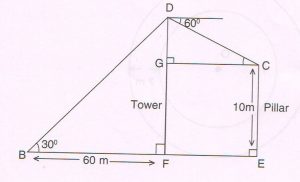
(D) A tower DF stands between a boy and a pillar CE. A boy at ‘B’ observes his father on the top ‘D’ of a tower at an angle of elevation of 30°. At the same time, his father observes the top ‘C’ of a pillar at an angle of depression of 60°.
The boy is 60 meters away from the foot of the tower. If the height of the pillar is 10 meters, find the distance between the feet of the tower and the pillar.
( Take \sqrt{3} = 1.7 )
Ans : Let FE = GC = x meters
And DG = y meters
So DF = DG + GF = y + 10 meters
In rt Δ DGC, tan 60° = \frac{DG}{GC}
\sqrt{3} = \frac{y}{x}
y = x \sqrt{3} meters …. (1)
In right ΔDFB,
tan 30° = \frac{DF}{BF}
\frac{1}{ \sqrt{3} } = y + \frac{10}{60}
y + 10 = \frac{60}{ \sqrt{3} }
y + 10 = \frac{ \frac{60}{ \sqrt{3} } }{ \frac{ \sqrt{3} }{ \sqrt{3} } }
= \frac{ \frac{60}{ \sqrt{3} } }{3}
y + 10 = 20 \sqrt{3}
y = 20 \sqrt{3} − 10
= 10 (2 \sqrt{3} − 1 )
= 10 × ( 2 × 1.7 − 1 )
= 10 × ( 3.4 − 1 )
= 10 × 24
y + 10 = 24
y = 24 − 10 = 14
y = x \sqrt{3}
x = \frac{y}{ \sqrt{3} }
= \frac{14}{ \sqrt{3} } × \frac{ \sqrt{3} }{ \sqrt{3} }
\frac{ 14 \sqrt{3} }{ 3 } = 14 × \frac{1.7}{3}
= \frac{23.8}{3} = 7.93
The distance is approx = 7.93 m
8 (A) Select and write the most appropriate alternative from those provided in the bracket :
1. The radius of the quadrant of a circle is 14 cm. Therefore its perimeter is ____ cm.
[ 22 , 28 , 39 , 50 ]
Ans : 50
2. Two cubes each of side 2 cm are joined end to end. The surface area of the resulting cuboid is ____ cm2.
[ 18 , 27 , 72 , 40 ]
Ans : 40
(B) Attempt each of the following :
1. The length of the minute hand of a clock is 10 cm. Find the distance traveled by its outer end in 6 minutes ( Take π = 3.1 )
Ans : 1 minute = \frac{360°}{60} = 6°
6 minutes = 6 × 6 = 36°
Distance travelled = \frac{Ø}{360} × 2 π r
= \frac{36}{360} × 2 × 3.1 × 10
= 6.2 cm
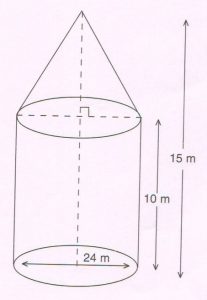
2. A tent of height 15 meters is in the form of a right circular cylinder of diameter 24 meters and height 10 meters, surmounted by a right circular cone of the same diameter. Find the slant height of the cone.
( Do not substitute the value of π )
Ans : Radius of the base of the cone, r = 12 m
Height of the cone, h = ( 15 − 10) m = 5 m
Let l be the slant height in meters
So l2 = h2 + r2
= 52 × 122
= 25 + 144
= 169
l = \sqrt{169}
= 13 m
Slant height is 13 meters
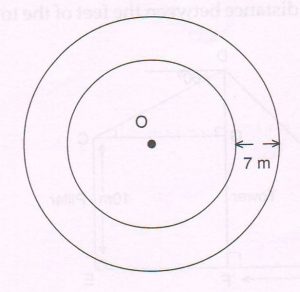
(C) The following figure shows a circular track whose inner circumference is 220 meters. If the track has a uniform width of 7 meters, find the area of the circular track. ( Take π = \frac{22}{7} )
Ans : Let inner radius be r meters
Inner circumference = 220 m
2 π r = 220
2 × \frac{22}{7} × r = 220
r = \frac{220 × 7}{2 × 22}
= 35 m
Area of the inner circle = π r2
= \frac{22}{7} × 35 × 35 m2
= 3850 m2 …. (1)
Let outer radius be R meters
Radius of outer circle = 35 + 7 = 42 m
Area of the outer circle = π R2
= \frac{22}{7} × 42 × 42
= 5544 m2 …. (2)
Area of the circular track = ( 5544 − 3850 ) m2
= 1594 m2
( D) A hollow metallic sphere of internal and external diameter 4 cm and 8 cm respectively is melted to form a solid cone of base diameter 8 cm. Find the height of the cone. ( Take π = \frac{22}{7} )
Ans : Inner radius of the sphere
= \frac{1}{2} × 4cm = 2cm
External radius of the sphere
= \frac{1}{2} × 8cm = 4cm
Volume of the metal of the sphere
= External volume − Internal volume
= \frac{4}{3} π × 43 − \frac{4}{3} π × 23
= \frac{4}{3} π ( 64 − 8 ) cm3
= \frac{4}{3} π × 56
= \frac{224 π}{3} cm3
This is melted to form a solid cone, whose number
= \frac{1}{3} π r2 h where h is the height of the cone.
\frac{1}{3} π r2 h = \frac{224}{3} π
4 × 4 × h = 224
h = \frac{224}{16}
= 14 cm
Height of the cone = 14 cm