GOA BOARD PAPER OCTOBER 2016
1 (A) Select and write the most appropriate alternative from those provided in the bracket :
The zeros of the quadratic polynomial 5u2 −25 are _____.
[ 0 and − \sqrt{5} , 5 and − 5 , \sqrt{5} and − \sqrt{5} , 0 and 15 ]
Ans : \sqrt{5} and − \sqrt{5}
(B) Attempt the following :
(i). Express the number 1386 as a product of its prime factors.
Ans :

1386 = 2 × 32 × 7 × 11
(ii). The product of two numbers is 1650 and their H.C.F. is 5. Find their LCM.
Ans : L.C.M. × H.C.F. = Product of the numbers
L.C.M. × 5 = 1650
L.C.M. = \frac{1650}{5}
= 330
(C) Assuming that \sqrt{3} is an irrational number, prove that :
11 − 2 \sqrt{5} is also an irrational number.
Proof : Let us assume, to the contrary that 11 − 2 \sqrt{3} is rational.
That is, we can find coprime a and b ( b ≠ 0 ) such that
11 − 2 \sqrt{3} = \frac{a}{b}
11 − \frac{a}{b} = 2 \sqrt{3}
\sqrt{3} = 11b − \frac{a}{2b}
Since a and b are integers, we get 11b − \frac{a}{2b} as rational.
So \sqrt{3} is rational. But this contradicts the fact that \sqrt{3} is irrational.
Our assumption that 11 − 2 \sqrt{3} is rational number is wrong
11 − 2 \sqrt{3} is irrational.
(D) If \sqrt{7} and − \sqrt{7} are two zeros of the polynomial
2x4 + 5x3 − 21x2 − 35x + 49 . Find the other two zeros.
Ans : Since \sqrt{7} and − \sqrt{7} are two zeros of the polynomial,
x − \sqrt{7} and x + \sqrt{7} are factors of the polynomial
( x − \sqrt{7} ) ( x + \sqrt{7} )
= x2 − 7 is a factor
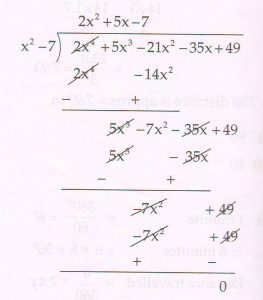
Other factors are given by
2x2 + 5x − 7 = 0
2x2 − 2x + 7x − 7 = 0
2x (x − 1 ) + 7 ( x − 1) = 0
( x − 1 ) (2x + 7 ) = 0
Either x − 1 = 0 or 2x + 7 = 0
x = 1 or x = − \frac{7}{2}
The other two zeros are 1 and − \frac{7}{2}
2(A) Select and write the most appropriate alternative from those provided in the bracket :
A die is thrown once. Therefore the probability of getting a number less than 4 on the top face of the die is ____.
( \frac{1}{2} , \frac{2}{3} , 1 , \frac{3}{2})
Ans : \frac{1}{2}
(B) Cards bearing numbers 5 to 20 are put in a box and mixed thoroughly. A card is drawn from the box at random. Find the probability that the number on the card drawn is:
(i). A single digit number
Ans : The number of possible outcomes, from 5 to 20 is 16
Number of favourable outcomes to get a single-digit number is 5
Probability of getting a single-digit number = \frac{5}{16}
(ii). A multiple of 2.
Ans : Number of favourable outcomes to get a multiple of 2
= \frac{8}{16}
= \frac{1}{2}
(C) Find the roots of ANY ONE of the following quadratic equations :
1. 5x2 − 19x + 18 = 0
( By using factorization method )
Ans : 5x2 − 19x + 18 = 0
5x2 − 10x − 9x + 18 = 0
5x ( x − 2) − 9 ( x − 2) = 0
( x − 2) ( 5x − 9 ) = 0
Either x − 2 = 0 OR 5x − 9 = 0
Either x = 2 OR x = \frac{9}{5}
The roots of the equation are 2 and \frac{9}{5}
2. x2 − 6x − 4 = 0 (deleted portion)
( By using completing the square method)
Ans : x2 − 6x = 4
Adding on both sides,
x2 − 6x + 9 = 4 + 9
L.T = − 6x × \frac{− 6x}{ 4 × 1} = 9
( x − 3)2 = 13
x − 3 = ± \sqrt{13}
x = 3 ± \sqrt{13}
Roots are 3 + \sqrt{13} and 3 − \sqrt{13}
(D) The hypotenuse of a right triangle is 2 cm less than thrice the shortest side. If the third side is 7 cm more than the shortest side, find the length of the hypotenuse of the right triangle.
Ans : Let the shortest side be x cm
Hypotenuse = ( 3x − 2) cm
Third side = ( x + 7) cm
By Pythagoras theorem
x2 + ( x + 7 )2 = ( 3x − 2 )2
x2 + x2 + 14x + 49 = 9x2 − 12x + 4
2x2 − 9x2 + 14x + 12x + 49 − 4 = 0
− 7x2 + 26x + 45 = 0
7x2 − 26x − 45 = 0
7x2 − 35x + 9x − 45 = 0
7x ( x − 5) + 9 ( x − 5) = 0
(x − 5) ( 7x + 9) = 0
Either x − 5 = 0 OR 7x + 9 = 0
x = 5 OR x = − \frac{9}{7}
Since side cannot be negative − \frac{9}{7} is discarded
Shortest side is 5 cm
And the hypotenuse is 3 × 5 − 2 = 13 cm
3(A) Select and write the most appropriate alternative from those provided in the bracket :
Three years hence, Rohan will be x years old and Sohan will be y years old. Therefore , the sum of their present ages is ____.
[ x + y − 3 ; x + y + 3 ; x + y + 6 ; x + y − 6 ]
Ans : x + y = − 6
(B) The following is a pair of linear equations in two variables:
2x + ky− 1 = 0
3x − 6y − 7 = 0
Answer the following questions with reference to the given pair of equations :
1. Write down the condition for no solution.
Ans : For no solution \frac{2}{3} = \frac{k}{− 6} ≠ \frac{− 1}{ − 7}
2. Find the value of k.
Ans : \frac{2}{3} = \frac{k}{ − 6}
k = 2 × \frac{( − 6)}{3}= − \frac{12}{3} = − 4
(C) Find the solution of ANY ONE of the following pairs of Linear equations :
1. 7x + 3y = 11 and 3x − 4y = 0
( By using elimination method )
Ans : 7x + 3y = 11 … (1)
3x − 4y = 10 …. (2)
4 × eq (1) 28x + 12y = 44
3 × eq. (2) 9x − 12y = 30
Adding, 37x = 74
x = \frac{74}{37} = 2
Substituting x = 2 in eq (1),
We get 7 × 2 + 3y = 11
3y = 11 − 14
3y = − 3
y = − 1
The solution is x = 2, y = − 1
2. 3x + 7y = 10 and 2x + y = 3
( By using substitution method)
Ans : 3x + 7y = 10 …. (1)
2x + y = 3 …. (2)
From (2), y = 3 − 2x
Substituting y in eq (1), we get
3x + 7 ( 3 − 2x) = 10
3x + 21 − 14x = 10
− 11x = − 11
x = 1
Substituting x = 1 in eq (1),
3 × 1 + 7y = 10
7y = 10 − 3
7y = 7
y = 1
Solution is x = 1 , y = 1
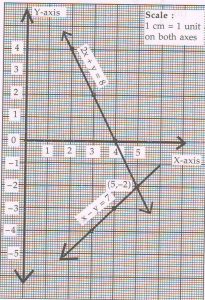
(D) Find the solution of the following pair of Linear equations graphically:
2x + y = 8 and x − y = 7
Rewrite the complete the following tables.
2x + y = 8
|
x |
|
|
|
|
y |
|
|
|
x − y = 7
|
x |
|
|
|
|
y |
|
|
|
( Plot at least three points for each line using a graph paper )
Ans : 2x + y = 8
|
x |
2 |
3 |
4 |
|
y |
4 |
2 |
0 |
x − y = 7
|
x |
2 |
3 |
4 |
|
y |
– 5 |
– 4 |
– 3 |
The graphical solution is x = 5 , y = − 2
4 (A) Select and write the most appropriate alternative from those provided in the bracket :
The 15th term of the Arithmetic Progression 3 , 8 , 13 , ….. is ____.
[ 13 , 24 , 73 , 120 ]
Ans : 73
(B) The following frequency distribution shows the monthly consumption of electricity of 30 houses in a locality. Find the median of the given data:
|
Monthly consumption ( in units) |
Number of houses |
|
55 − 65 |
5 |
|
65 − 75 |
7 |
|
75 − 85 |
10 |
|
85 − 95 |
8 |
Ans : n = 30 \frac{n}{2} = 15. So 75 − 85 is the median class
l = 75, f = 10, h = 10
Cf = 5 + 7 = 12, cumulative frequency of the class preceding the median class
Median = l + [ \frac{n}{2} − \frac{Cf}{f} ] × h
= 75 + [ \frac{15 − 12}{10} ] × 10
= 75 + 3
Median = 78
(C) Find the sum of the even natural numbers lying between 10 and 100.
Ans : Even natural numbers between 10 and 100 are 12 , 14 , 16 , 18 , 20 , ……, 94 , 96 , 98.
Here, a = 12 ,d = 2.
Let the number of terms be n. The nth term is 98.
an= a + ( n − 1) d
98 = 12 ( n − 1) 2
98 − 12 = 2 ( n − 1)
\frac{86}{2} = n − 1
43 = n − 1
n = 43 + 1 = 44
Now S = \frac{n}{2} [ 2a + ( n − 1) d ]
= \frac{44}{2} [ 2 × 12 + ( 44 − 1) × 2 ]
= 22 [ 24 + 86 ]
= 2420
Sum of the even natural numbers lying between 10 and 100 is 2420.
(D) The following table shows the donation collected by a club:
Taking the classmark denoted by ‘a’ of the class interval 100 − 150 as the assumed mean, rewrite and complete the table and also find the mean of the donation collected by the assumed mean method.
Ans :
Mean, by an assumed mean method
= a + \frac{∑fidi}{∑fi}
= 125 + \frac{1350}{45}
= 125 + 30
Mean= 155
5 (A) Select and write the most appropriate alternative from those provided in the bracket :
The radius of a circle O is 6 cm. A tangent PR at point P on the circle meets a line drawn from O at a point R such that OR = 10 cm. Therefore the length of PR = _____ cm.
[ 8 , 16 , 64 , 136 ]
Ans : 8 cm
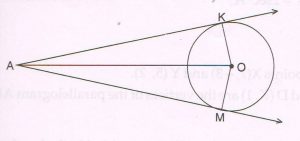
(B) Given: Point O is the center of a circle. Two tangent segments AK and AM are drawn from external “ point A” to the circle at K and M respectively.
Prove that: AK = AM.
( Write only the proof with reasons )
Proof : The tangents to the circle from an external point are perpendicular to the radii at the point of contact.
AK ⊥ OK at K and AM ⊥ OM at M
In right Δs AKO and AMO,
AO = AO ( common side )
OK = OM ( radii of the same circle)
ΔAKO ≅ ΔAMO ( Hypotenuse- side theorem )
AK = AM ( c.p.c.t )
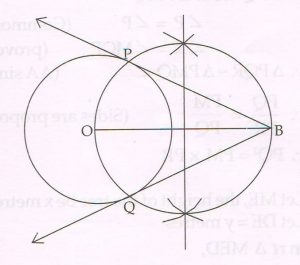
(C) Draw a circle with center O and radius 2.5 cm. Then take a point B at a distance of 6.7 cm from the center of the circle. Using a pair of compass and ruler, construct two tangents BP and BQ to the circle. Measure and state the length of tangent segments.
Ans :
The length of each tangent segment is 6.2 cm
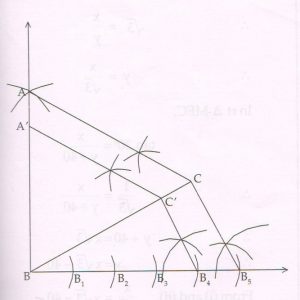
(D) Using a pair of compass and ruler, construct Δ ABC with sides BC = 6.5 cm , AB = 5cm and ∠ ABC = 60°. Then construct Δ A ‘BC’ whose sides are \frac{4}{5} of the corresponding sides of Δ ABC.
Ans :
6 (A) Select and write the most appropriate alternative from those provided in the bracket :
If B is an acute angle, then cos2 \frac{( 90° − B)}{sin² B} = _____.
[− 1 , 1 , cot B , cot2 B ]
Ans : 1
(B) Attempt ANY ONE of the following :
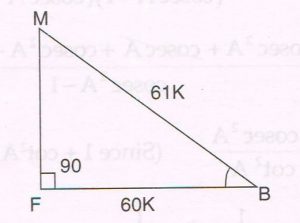
1. In Δ BFM, ∠F = 90° and cos B = \frac{60}{61}, then find:
(a) The length of FM
(b) The value of tan B.
(c) The value of sec M.
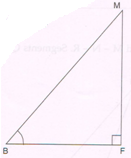
Ans :
(a) cos B = \frac{60}{61}. Let FB = 60k and MB = 61k
By Pythagoras theorem
FM2 + FB2 = MB2
FM2 + ( 60k)2 = ( 61 k)2
FM2 = 3721 k2 − 3600 k2
= 121 k2
FM = \sqrt{121k²}
= 11 k
(b) tan B = \frac{FM}{FB}
= \frac{11k}{60k}
= \frac{11}{60}
(c) sec M = \frac{1}{cos M}
= \frac{1}{ \frac{MF}{MB} }
= \frac{MB}{MF}
= \frac{61k}{11k}
= \frac{61}{11}
2. Evaluate the following expression using known numerical values of trigonometrical ratios :
2sec2 30° − \sqrt{3} cot 60° + cos2 30°.
Ans : 2sec2 30° − \sqrt{3} cot 60° + cos2 30°
= 2 × ( \frac{2}{ \sqrt{3} } )2 − \sqrt{3} × \frac{1}{ \sqrt{3} } + ( \frac{ \sqrt{3} }{ 2} )²
= 2 × \frac{4}{3} − 1 + \frac{3}{4}
= 32 − 12 + \frac{9}{3} × 4
= \frac{29}{12}
(C) Prove the following identity:
\frac{cosec A}{cosec A - 1} + \frac{cosec A}{cosecA + 1} = 2sec2 A
Ans : L.H.S
= \frac{cosec A}{cosec A - 1} + \frac{cosec A}{cosecA + 1}
= \frac{cosec A ( cosec A + 1) + cosecA ( cosec A - 1 )}{(cosec A - 1) ( cosec A + 1 )}
= \frac{2 cosec² A}{cot² A } ( since 1 + cot² A = cosec² A)
= 2 × \frac{1}{sin² A } × \frac{1}{ \frac{cos² A}{sin² A} }
= 2 × \frac{1}{sin² A } × \frac{sin² A}{cos² A }
= 2sec2 A
= R.H.S.
(D) Attempt each of the following :
1. Find the distance between the points X ( 7 , − 3) and Y (5 , 2 ).
Ans : XY = \sqrt{( 7 − 5)² + ( − 3 − 2)²}
= \sqrt{2² + (− 5)²}
= \sqrt{4 + 25}
= \sqrt{29}
2. If A ( − 1 , 1 ), B ( − 3, − 2) , C ( 1 , − 2) and D ( k , 1) are the vertices of the parallelogram ABCD, find the value of k.
Ans : AD = BC ( opp. sides of a \| gm )
AD2 = BC2
( − 1 − k)2 + (1 − 1)2 = ( − 3 − 1 )2 + ( − 2 + 2)2
1 + 2k + k2 + 0 = 16 + 0
k2 + 2k − 15 = 0
( k + 5) ( k − 3 ) = 0
Either k + 5 = 0 OR k − 3 = 0
k = − 5 OR k = 3
7(A) Select and write the most appropriate alternative from those provided in the bracket :
If Δ ABC ∼ ΔPQR and ar( ABC) = 16 ar ( PQR) , then the value of \frac{PQ}{AB} = ____.
( \frac{1}{16} , \frac{1}{4} , 4 , 16 )
Ans : \frac{1}{4}
(B) With reference to the given figure and given condition, write only the proof with reasons of the following theorem.
Given: In ΔPQR, ∠ PQR = 90° QS ⊥ PR and S lies on PR
Prove that : PQ2 + QR2 = PR2
Proof: Δ PSQ ∼ Δ PQR ( AA similarity )
\frac{PS}{PQ} = \frac{PQ}{PR} ( sides are proportional )
PS × PR = PQ2 …. (1)
Δ QSR ∼ Δ PQR ( AA similarity )
\frac{SR}{QR} = \frac{QR}{PR}
SR × PR = QR2 ….. (2)
From (1) and (2)
PS × PR + SR × PR = PQ2 + QR2
PR ( PS + SR) = PQ2 +QR2
PR × PR = PQ2 + QR2
PQ2 + QR2 = PR2
(C) In Δ PQN, PQ = PN , P − M − N and M − N − R.
Segments QM and QR are drawn such that ∠NQM = ∠ NQR.
Prove that : PQ2 = PM × PR
Proof :
∠ QNM = ∠ R + ∠ RQN ( exterior angle property)
∠ NQP = ∠ NQM + ∠ MQP
But ∠ QNM = ∠ NQP ( since PQ = PN )
∠ R + ∠ RQN = ∠NQM + ∠ MQP
But ∠RQN = ∠ NQM ( given )
∠ R = ∠ MQP …. (1)
In Δ PQR and Δ PMQ
∠P = ∠P ( common angle )
∠R = ∠ MQP ( proved in (1) )
ΔPQR ∼ Δ PMQ ( AA similarity )
\frac{PQ}{PR} = \frac{PM}{PQ} ( Sides are proportional )
PQ2 = PM × PR
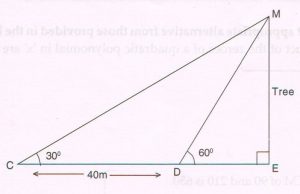
(D) A man standing on the bank ‘D’ of a river, observes the angle of elevation of the top ‘M’ of a tree ‘ME’ standing on the opposite bank, as 60°. When he moves 40 meters away from the bank along the horizontal line, through the base as shown in the figure, he finds the angle of elevation of the top ‘M’ to be 30°. Find the height of the tree.
( Take \sqrt{3} = 1.73 )
Ans : Let ME, the height of the tree be x meters
Let DE = y meters
In right Δ MED,
tan 60° = \frac{x}{y}
\sqrt{3} = \frac{x}{y}
y = \frac{x}{ \sqrt{3} } …. (1)
In right Δ MEC,
tan 30° = \frac{x}{y} + 40
\frac{1}{ \sqrt{3} } = \frac{x}{y} + 40
y + 40 = x \sqrt{3}
y = x \sqrt{3} − 40 …. (2)
From (1) and (2), \frac{x}{ \sqrt{3} } = x \sqrt{3} − 40
Multiply by \sqrt{3} , x = 3x − 40 \sqrt{3}
3x − x = 40 \sqrt{3}
2x = 40 \sqrt{3}
x = 40 × \frac{1.73}{2}
= 34.60
The height of the tree is 34.6 meters
8(A) Select and write the most appropriate alternative from those provided in the bracket :
1. Two concentric circles have their diameters of 16 cm and 12 cm. Therefore the width of the ring is ____ cm.
[ 2 , 4 , 14 , 28 ]
Ans : 2
2. The area of four walls of a hall in the form of a cuboid is 220m2 and the height of the hall is 5m. Therefore the perimeter of the floor of the hall is ____ meters.
[ 11 , 22 , 44 , 88 ]
Ans : 22
(B) Attempt each of the following :
1. A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the minor segment of the circle. ( Take π = 3.1 )
Ans : Area of minor segment = Area of the quadrant − Area of triangle
= \frac{1}{4} π r2 − \frac{1}{2} r2
= \frac{1}{4} × 3.1 × 10 × 10 − \frac{1}{2} × 10 × 10
= \frac{1}{4} × 310 − 50
= 77.5 − 50
= 27.5 cm2
2. The base area and height of a right circular cone are 154 cm2and 6 cm respectively. Find the volume of the cone.
Ans : base area of cone = 154 cm2
Height = 6 cm
Volume of cone = \frac{1}{3} × π r2 × h
= \frac{1}{3} × 154 × 6
= 308 cm3
(C) A square field and an equilateral triangular park have equal perimeters. If the cost of weeding the square field at the rate of Rs 5 per square meter is Rs 720 find the cost of fencing the equilateral triangular park at the rate of Rs 55 per meter.
Ans : Area of the square field
= \frac{720}{4} = 144 meters
S2 = 144 where S is the side of the square.
S = \sqrt{144} = 12 meters
The perimeter of the square field = 4 × 12 = 48 meters
∴ The perimeter of the equilateral triangular park = 48 meters
Cost of fencing the triangular park = 48 × Rs 55 = Rs 2640
(D) 12 hollow metallic spheres of the same size are made by melting a solid metallic cylinder of base diameter 16 cm and height 14 cm. If the inner radius of each hollow sphere is equal to the thickness of the hollow sphere, find the inner radius of the hollow sphere
( Take π = \frac{22}{7} )
Ans : Volume of the solid metallic cylinder = π R2 h
= \frac{22}{7} × 8 × 8 × 14 cm3
= 44 × 64 cm3
= 2816 cm3
Let the inner radius of the hollow sphere be r cm
Outer radius is r + r = 2r cm
Volume of each hollow metallic sphere = outer volume – inner volume
= \frac{4}{3} π ( 2r)3 − \frac{4}{3} π r3
= \frac{4}{3} π [ 8r3 − r3 ]
= \frac{4}{3} × 7 r3 cm3
Now volume of 12 hollow spheres = Volume of the solid cylinder
12 × \frac{4}{3} × \frac{22}{7} × 7 r3 = 2816
r3 = \frac{2816}{4} × 4 × 22
= 22 × 8 × 8 × \frac{2}{4} × 4 × 22
= 8
r = \sqrt[3]{8} = 2
Inner radius of the hollow sphere is 2 cm.