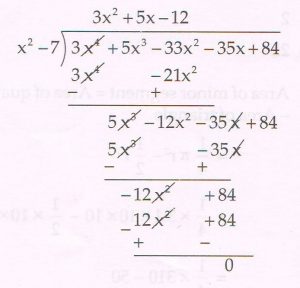Goa Board paper MARCH 2017
1 (A) Select and write the most appropriate alternative from those provided in the bracket :
If the sum and the product of the zeroes of a quadratic polynomial in ‘x’ are ‘3’ and ‘0’, then the quadratic polynomial is ____.
(a) x2 + 3x
(b) x2 − 3x
(c) x2 + 3x − 3
(d) x2 − 3x + 3
Ans : (b) x2 − 3x
(B) Attempt the following :
1. Find the HCF if LCM of 90 and 210 is 630.
Ans : Product of numbers = HCF × LCM
90 × 210 = HCF × 630
HCF = \frac{90 × 210}{630}
HCF = 30
2. Express the number 3150 as a product of its factors.
Ans : Prime Factors Tree of 3150
3150 ÷ 2 = 1575
1575 ÷ 3 = 525
525 ÷ 3 = 175
175 ÷ 5 = 35
35 ÷ 5 = 7
7 ÷ 7 = 1
∴ 3150 = 2 × 32 × 52 × 7
(C) Assuming that \sqrt{2} is an irrational number, prove that 3 + 5 \sqrt{2} is also an irrational number.
Ans : Let us assume, to the contrary, that 3+ 5 \sqrt{2} is rational.
That is, we can find coprime a and b ( b ≠ 0 ) such that
3 + 5 \sqrt{2} = \frac{a}{b − 3}
5 \sqrt{2} = \frac{90 × 210}{630}
5 \sqrt{2} = \frac{( a − 3b)}{b}
\sqrt{2} = \frac{( a − 3b)}{5b}
Since a and b are integers,
\frac{( a − 3b)}{5b} is rational,
\sqrt{2} is rational, contradicting the fact that \sqrt{2} is irrational
Our assumption that 3 + 5 \sqrt{2} is rational is wrong,
3 + 5 \sqrt{2} is irrational
(D) If the two zeroes of the polynomial 3x4 + 5x3 − 33x2 − 35x + 84 are \sqrt{7} and − \sqrt{7}, then find the other two zeroes.
Ans : Since two zeros are \sqrt{7} and − \sqrt{7} ,
( x − \sqrt{7} ) ( x + \sqrt{7} )
= x2 − 7 is a factor of the given polynomial
3x2 + 5x − 12 is the other factor
Factorising it we get
3x2 + 9x − 4x − 12 = 0
3x ( x + 3 ) − 4 ( x + 3 ) = 0
(x + 3 ) ( 3x − 4) = 0
x + 3 = 0 OR 3x − 4 = 0
x = − 3 OR x = \frac{4}{3}
The other two zeros are − 3 and \frac{4}{3}
2 (A) Select and write the most appropriate alternative from those provided in the bracket :
In a throw of a dice, the probability of getting an old prime number on the top face is ___.
(a) 2
(b) \frac{3}{2}
(c) \frac{1}{2}
(d) \frac{1}{3}
Ans : (d) \frac{1}{3}
(B) The king, queen and jack of diamonds are removed from a deck of 52 playing cards and the remaining cards are well shuffled. If one card at random is selected from the well-shuffled cards, find the probability that the card is drawn is :
Ans : When 3 cards are removed, the number of possible outcomes is 52 − 3 = 49
1. A king
Ans : To get a king, the number of favourable outcomes is 3.
P(E) = \frac{Number \thinspace \thinspace of \thinspace outcomes \thinspace \thinspace favourable}{ Number \thinspace \thinspace of \thinspace \thinspace all \thinspace \thinspace possible \thinspace \thinspace outcomes}
The probability of getting a king is \frac{3}{49}.
2. A diamond
Ans : To get a diamond card, the number of favourable outcomes is 10.
P(E) = \frac{Number \thinspace \thinspace of \thinspace outcomes \thinspace \thinspace favourable}{ Number \thinspace \thinspace of \thinspace all possible \thinspace \thinspace outcomes}
The probability of getting a diamond card is \frac{10}{49}.
(C) Attempt ANY ONE of the following :
1. 6x2 − 5x − 21 = 0
( By factorization method)
Ans : 6x2 − 5x − 21 = 0
6x2 − 14x + 9x − 21 = 0
2x ( 3x − 7 ) + 3 ( 3x − 7 ) = 0
(3x − 7 ) (2x + 3 ) = 0
Either 3x − 7 = 0 Or 2x + 3 = 0
Either x = \frac{7}{3} Or x = − \frac{3}{2}
Roots are \frac{7}{3} and − \frac{3}{2}
2. 3x2 − 10x + 8 = 0
( By using the quadratic formula )
Ans : 3x2 − 10x + 8 = 0
Here a =3 , b = − 10 , c = 8
b2 − 4ac = ( − 10)2 − 4 × 3 × 8
= 100 − 96= 4
Roots are = \frac{(− 10) ± \sqrt{4} }{2 × 3}
= \frac{10 ± 2 }{26}
\frac{ (10 + 2) }{6} and \frac{(10 − 2 ) }{6}
Roots are 2 and \frac{4 }{3}
(D) The perimeter of a right angled triangle is 60 cm and its hypotenuse is of length 25 cm. Find the length of the other two sides of the triangle.
Ans : Total length of the two sides containing the right angle
= 60 − 25 = 35 cm
If one side is x cm, then the other is ( 35 − x) cm
By Pythagoras’ theorem
x2 + ( 35 − x )2 = 252
x2 + 1225 − 70x + x2 = 625
2x2 − 70x − 625 + 1225 = 0
2x2 − 70x + 600 = 0
x2 − 35x + 300 = 0
x2 − 20x − 15x + 300 = 0
x (x − 20 ) − 15 (x − 20 ) = 0
( x − 20 ) (x − 15 ) = 0
x − 20 = 0 Or x − 15 = 0
x = 2 Or x = 15
The two sides containing the right angle are 20 cm and 15 cm.
3 (A) Select and write the most appropriate alternative from those provided in the bracket :
The ages of A and B three years ago were ‘x’ and ‘y + 2’ years, therefore the sum of their ages 4 years hence will be ____ years.
(a) x + y − 12
(b) x+ y + 12
(c) x + y + 16
(d) x + y − 16
Ans : (c) x + y + 16
(B) For the following pairs of linear equations :
x + 3y = 5
( k + 1 )x + 9y = 8k − 1
Answer the following questions with reference to the given pair of equations :
Ans : x + 3y − 5 = 0
(k + 1) x + 9y − ( 8k − 1) = 0
1. Write down the condition for infinitely many solutions.
Ans : For infinitely many solutions
\frac{1}{k + 1} = \frac{3 }{9} = \frac{ − 5}{− (8k − 1)}
2. Find the value of k.
Ans : 1 × 9 = 3 ( k + 1)
9 = 3 k + 3
9 − 3 = 3k
k = \frac{6 }{3} = 2
(C) Attempt ANY ONE of the following :
1. 3x − 4y = 10 and 5x + y = 9
( By elimination method)
Ans : 3x − 4y = 10 …. (1)
5x + y = 9 …. (2)
________________
Eq. (2) × 4, 20x + 4y = 36 …. (3)
Adding eq (1) and (3), 23 x = 46
x = \frac{46 }{23}
x = 2
Substitute x = 2 in eq (2),
5 × 2 + y = 9
y = 9 − 10
y = − 1
The solution is x = 2 , y = − 1 .
2. 2x − 3y = 11 and 7x + 2y = 26
( By cross multiplication method )
Ans: 2x − 3y − 11 = 0
7x + 2y − 26 = 0
By cross multiplication method,
\frac{x }{− 3 × (− 26) − 2× ( − 11)}
= \frac{y }{7 × (− 11) − 2 × (− 26)}
= \frac{1 }{2 × 2 − 7 ( − 3)}
\frac{x }{78 + 22}
= \frac{y }{− 77 + 52}
= \frac{1}{4 + 21} \frac{x }{100}
= \frac{y }{25}
= \frac{1 }{25}
\frac{x }{100} = \frac{1 }{25} gives x = 4
and \frac{y }{ − 25} = \frac{1}{25} gives y = − 1
The solution is x = 4 , y = − 1
(D) A car and a motorcyclist start from the same spot and move in the opposite direction. After 2 hours the distance between them is 140 km. If they had travelled in the same direction, then the distance between them would have been 20 km after 2 hours. Find the speed of the car and the motorcyclist.
Ans : Let the speed of the car be x km / hr
And the speed of the motorcycle be y km / hr
Since Distance = Speed × Time
After 2 hours, distance covered by the car is 2 km
And distance covered by the motorcycle is 2y km
In the opposite direction, we get
2x + 2y = 140 …. (1)
In the same direction, we get
2x − 2y = 20 …. (2)
Solving we get , 4x = 160
x = 40
Substitute x = 40 in eq (1), we get
2 × 40 + 2y = 140
2y = 140 − 80
= 60
y = 30
Speed of the car is 40 km /hr.
And the speed of the motorcycle is 30 km/hr.
4 (A) Select and write the most appropriate alternative from those provided in the bracket :
In an Arithmetic Progression, if the first term is 8 and the common difference is 4, then the ninth term of the A.P. is ____.
(a) 4
(b) 20
(c) 40
(d) 64
Ans : (c) 40
(B) Find the sum of the first 20 terms of an Arithmetic Progression in which the third term is 7 and seventh term is 2 more than thrice its third term.
Ans : a3 = 7 and a7 = 23
a + 2d = 7 and a + 6d = 23
Solving, 6d − 2d = 23 − 7
4d = 16
d = 4
a + 2d = 7 gives a + 2 × 4 = 7
a = − 1
Now Sn = \frac{n }{2} [ 2a + ( n − 1) d ]
S20 = \frac{20 }{2} [ 2 ( − 1) + ( 20 − 1) 4 ]
= 10 [ − 2 + 76 ]
= 10 × 74
S20 = 740
Sum of the first 20 terms is 740
(C) The following table shows the marks scored by 60 students in a Mathematics test out of 80 :
Rewrite and complete the table and find the mean marks scored by the direct method.
Ans :
Mean marks = \frac{∑fixi }{∑fi}
= \frac{2610 }{60}
The mean marks scored = 43.5
(D) The following table shows the marks scored by 70 students :
|
Marks |
Frequency |
|
40 − 50 |
14 |
|
50 − 60 |
12 |
|
60 − 70 |
18 |
|
70 − 80 |
15 |
|
80 − 90 |
6 |
|
90 − 100 |
5 |
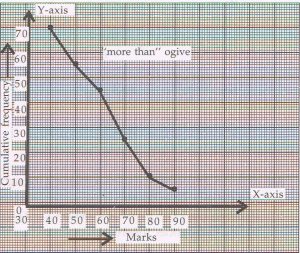
Convert the distribution to a more than type cumulative frequency distribution, and draw its ogive.
Ans :
|
Marks |
Cumulative frequency |
|
More than 40 |
70 |
|
More than 50 |
56 |
|
More than 60 |
44 |
|
More than 70 |
26 |
|
More than 80 |
11 |
|
More than 90 |
5 |
5(A) Select and write the most appropriate alternative from those provided in the bracket :
From a point P outside a circle, the length of the tangent segment to the circle is 21 cm and the distance of P from the centre is 29 cm. Therefore the length of the diameter of the same circle is _____.
(a) 10 cm
(b) 20 cm
(c) 40 cm
(d) 50 cm
Ans : (c) 40 cm
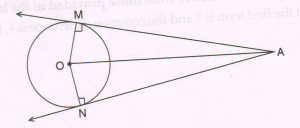
(B) Given: Point ‘O’ is the centre of a circle. Two tangents AM and AN are drawn from the external point A to the circle at M and N respectively.
Prove that : AM = AN.
( Write only the proof with reasons )
Proof : Tangents are perpendicular to the radii at the points of the contract,
∠ OMA and ∠ ONA are right angles.
In rt. Δ OMA and Δ ONA
OA = OA ( common side)
OM = ON ( radii of the same circle)
Δ OMA ≅ ΔONA ( hypotenuse-side theorem )
AM = AN ( c.p.c.t)
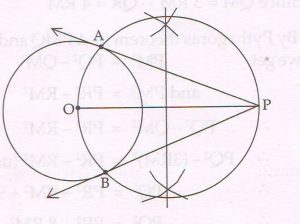
(C) Draw a circle with centre ‘O’ and radius 3 cm, then take a point P at a distance of 7 cm from the centre of the circle. Using a pair of compass and ruler only, construct two tangents PA and PB to the circle. Measure and state the length of the tangent segments.
Ans :
The length of each tangent segment is 6.3 cm.
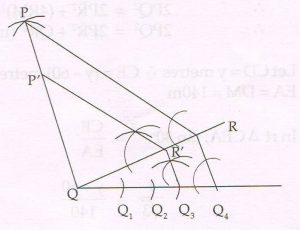
(D) Using a pair of compass and ruler, construct Δ PQT with sides PQ = PR = 6 cm and QR = 5 cm. Then construct Δ P’QR’ whose sides are \frac{3}{4} of the corresponding sides of ΔPQR.
Ans :
6 (A) Select and write the most appropriate alternative from those provided in the bracket :
If \frac{1 }{cosec} = cosec 40°, then the value of x is ____.
(a) 40°
(b) 50°
(c) 60°
(d) 90°
Ans : (b) 50°
(B) Prove the following identity :
1. \frac{sin ∅ + cos ∅ }{sin ∅ − cos ∅} + \frac{sin ∅ − cos ∅ }{sin ∅ + cos ∅} = \frac{2 }{2 sin² ∅ − 1}
Ans :
L.H.S. = \frac{( sin ∅ + cos ∅ )² + ( sin ∅ − cos ∅)²}{ ( sin ∅ − cos ∅ ) ( sin ∅ + cos ∅ )}
= \frac{sin² ∅ + 2 sin ∅ cos ∅ + cos² ∅ + sin² ∅ − 2 sin ∅ − 2 sin ∅ cos ∅ + cos² ∅ }{ sin² ∅ − cos² ∅}
= \frac{sin² ∅ + cos² ∅)+ ( sin² ∅ + cos² ∅ ) }{sin² ∅ − ( 1 − sin² ∅ )}
Using sin2 Ø + cos2 Ø= 1
= 1 + \frac{1 }{sin² Ø − 1} + sin² Ø
= \frac{2 }{2 sin² Ø − 1}
= R.H.S.
(C) Attempt ANY ONE of the following :
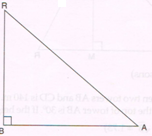
1. In Δ ABR, ∠ B = 90°. If tan A = \frac{15 }{8} , then find :
(a) The length of AR
(b) the value of cos A
(c) The value of sec R
Ans : tan A = \frac{15 }{8} BR = 15k and BA = 8k
(a) By Pythagoras theorem,
AR2 = BR2 + BA2
= ( 15k)2 + ( 8k)2
= 225k2 + 64k2
= 289k2
AR = \sqrt{289k²}
= 17k
(b) cos A = \frac{ adj side}{hyp}
= \frac{BA }{AR}
= \frac{15k }{17k}
= \frac{15 }{17}
(c) sec R = \frac{1 }{cos R}
= \frac{hyp }{adj sides to ∠ R}
= \frac{AR }{BR}
= \frac{17 }{8 k}
= \frac{17}{8}
= \frac{9 }{40}
OR
2. Evaluate : sin 60° + cos 30° + sin 30° cos 60°.
Ans : sin 60° + cos 30° + sin 30° cos 60°
= \frac{ \sqrt{3} }{2} + \frac{ \sqrt{3} }{2} + ( \frac{1}{2} × \frac{1}{2} )
= (2 × \frac{ \sqrt{3} }{2}) + \frac{1}{4} = \frac{1}{4}+ \sqrt{3}
(D) Attempt each of the following :
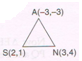
1. Find the area of Δ ASN with A ( − 3, − 3), S ( 2 , 1) and N ( 3 , 4).
Ans : Area of Δ ASN =
\frac{1}{2} [ ( − 3) ( 1 − 4) + 2 (4 + 3) + 3 ( − 3 ) ]
\frac{1}{2} [ 9 + 14 − 12 ]
= \frac{11}{2}
Area of Δ ASN = 5.5 square units.
2. Find the relation between x and y such that point P ( x , y) is equidistant from A ( 3 , 7)
and B ( 2 , 2).
Ans : PA = PB
PA2 = PB2
( x − 3)2 + ( y − 7)2 = ( x − 2)2 + ( y − 2)2
x2 − 6x + 9 + y2 − 14y + 49 = x2 − 4x + 4 + y2 − 4y + 4
− 6x + 4x − 14y + 4y = 4 + 4 − 9 − 49
− 2x − 10y = − 50
x + 5y = 25
7 (A) Select and write the most appropriate alternative from those provided in the bracket :
ΔABC ∼ ΔPQR. If BC = 2.4 cm, QR = 3.6 cm, then AC = _____.
(a) 2 cm
(b) 4 cm
(c) 8 cm
(d) 12 cm
Ans : (b) 4 cm
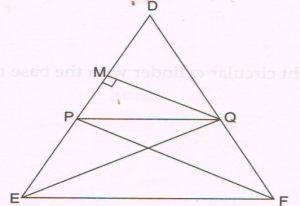
(B) Given : In Δ DEF, PQ \| EF where the points P and Q lie on DE and DF respectively and QM ⊥ DE.
Prove that : \frac{DP}{PE} = \frac{DQ}{QF}
( Write only the proof with reasons)
Proof: Let PN ⊥ DQ
ar ( DPQ) = \frac{1}{2} × base × height
= \frac{1}{2} × DP × QM
ar ( EPQ ) = \frac{1}{2} × EP × QM
\frac{ar ( DPQ)}{ar ( EPQ)}
= \frac{ \frac{1}{2}× DP × QM }{ \frac{1}{2} × EP × QM}
= \frac{DP}{PE} …. (1)
Also ar( DPQ) = \frac{1}{2} × DQ × PN
And ar( FPQ) = \frac{1}{2} × QF × PN \frac{ar ( DPQ)}{ar ( FPQ)}
= \frac{ \frac{1}{2}×DQ × PN }{ \frac{1}{2} × QF × PN}
= \frac{DQ}{QF} …. (2)
Now Δ EPQ and Δ FPQ are on the same base PQ and between the same parallels PQ and EF
ar ( Δ EPQ) = ar (Δ FPQ) …. (3)
From (1), (2) and (3),
\frac{DP}{PE} = \frac{DQ}{QF}
(C) Given : The perpendicular from vertex P on the side QR of Δ PQR intersects QR at M such that QM = 3 RM.
Prove that : 2 PQ2 = 2 PR2 + QR2
( Write only the proof with reasons)
Proof : Since QM = 3 RM QR = 4 RM …. (1)
By Pythagoras theorem in Δ PMQ and Δ PMR
We get PM2 = PQ2 − QM2
And PM2 = PR2 − RM2
PQ2 − QM2 = PR2 − RM2
PQ2 − ( 3RM)2 = PR2 − RM2 [ using (1) ]
PQ2 = PR2 − RM2 + 9 RM2
PQ2 = PR2 + 8 RM2
Multiply by 2 we get 2PQ2 = 2PR2 + 16 RM2
2 PQ2 = 2PR2 + ( 4RM)2
2PQ2 = 2PR2 = QR2 [ using (1) ]
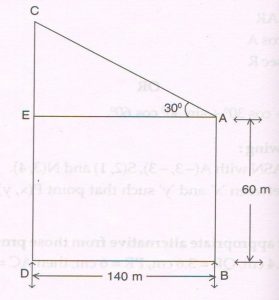
(D) The horizontal distance between two towers AB and CD is 140 m. The angle of elevation of the top of the tower CD when seen from the top of tower AB is 30°. If the height of the tower AB is 60 m find the height of the tower CD.
( Take \sqrt{3} = 1.73 )
Ans : Let CD = y meters CE = ( y − 60) meters
EA = DM = 140m
In right Δ CEA, tan 30° = \frac{CE}{EA}
\frac{1}{ \sqrt{3} } = y − \frac{60}{140}
140 = \sqrt{3} y − 60 \sqrt{3}
\sqrt{3} y = 140 + 60 \sqrt{3}
y = \frac{140}{ \sqrt{3} } + ( \frac{60}{ \frac{ \sqrt{3} }{ \sqrt{3} } } )= \frac{140}{ \sqrt{3} } + 60
= \frac{140}{1.73} + 60
= 80.9 + 60
= 140.9
The height of the tower CD is 140.9 meters
8 (A) Select and write the most appropriate alternative from those provided in the bracket :
1. A circular grass lawn of 35 m in radius has a path 7 m wide running around it on the outside. The area of the path is ____.
(a) 393 p m2
(b) 539 p m2
(c) 593 p m2
(d) 1176 p m2
Ans : (c) 539 p m2
2. The lateral surface area of a right circular cylinder with the base radius 7 cm and height 10 cm is _____.
(a) 204 cm2
(b) 240 cm2
(c) 404 cm2
(d) 440 cm2
Ans : (d) 440 cm2
(B) Attempt each of the following :
1. A sector of 120° cut from a circle has an area of 9 \frac{3}{7} cm2, then find the radius of the circle.
Ans : Area of the sector = \frac{Ø}{360} × π × r2
\frac{66}{7} = \frac{120}{360} × \frac{22}{7} × r2
r2 = 66 × \frac{3}{22}
r = 3
Radius of the circle = 3 cm
2. The diameter of a copper sphere is 6 cm. It is beaten and drawn into a wire of diameter 0.2 cm. Find the length of the wire drawn.
Ans : Volume of the sphere = Volume of the cylindrical wire
\frac{4}{3} π × R3 = π × r2 × h
\frac{4}{3} × 3 × 3 = \frac{1}{10} × \frac{1}{10} × h
4 × 9 × 100 = h
h = 3600 cm
Length of the wire is 3600 cm or 36 meters.
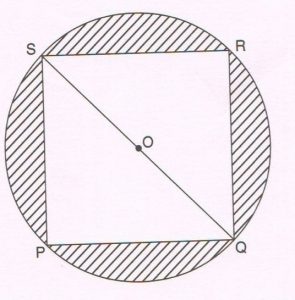
(C) PQRS is a square inscribed in a circle with centre O. If PQ = 8 cm, find the area of the shaded region. ( Take π = \frac{22}{7} )
Ans : By Pythagoras theorem,
SQ2 = PS2 + PQ2
= 82 + 82
= 64 + 64
= 128
SQ = \sqrt{128} = 8 \sqrt{2}
Radius of the circle is 4 \sqrt{2} cm
Area of the circle = π r2 = \frac{22}{7} × 4 \sqrt{2} × 4 \sqrt{2}
= 100.6 cm2
Area of the square = PQ2 = 82 = 64 cm2
Area of the shaded region = Area of the circle − Area of the square
= ( 100.6 − 64 )
= 36.6 cm2
(D) A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top which is open is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel.
Ans : \frac{1}{4} volume of the cone = volume of the number of spherical shots
\frac{1}{4} × \frac{1}{3} π R2 h
= N × \frac{4}{3} × π r3
\frac{1}{2} × 52 × 8
= N × \frac{4}{3} × \frac{5}{10} × \frac{5}{10} × \frac{5}{10}
25 × 8 × 3 × \frac{8}{12} × 4 = N
N = 100
Number of lead shots dropped in the vessel is 100.