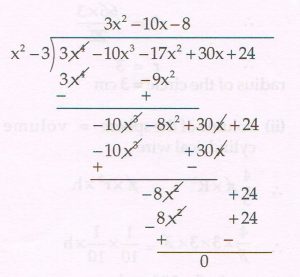Goa Board Paper OCTOBER 2018
1(A) Select and write the most appropriate alternative from those given below :
If a and b are the zeros of a quadratic polynomial 2x2 − 5x − 7, then the value of \frac{1}{a} +\frac{1}{b} = ____.
(a) \frac{5}{7}
(b) \frac{7}{5}
(c) − \frac{5}{7}
(d) − \frac{7}{5}
Ans : (c) − \frac{5}{7}
(B) Use Euclid’s division algorithm to find the HCF of 81 and 135.
Ans : By applying Euclid’s division algorithm
135 = 81 × 1 + 54
81 = 54 × 1 + 27
54 = 27 × 2 + 0
HCF of 81 and 135 is 27.
(C) Assuming that \sqrt{7} is an irrational number, prove that 5 − 4 \sqrt{7} is also an irrational number.
Ans : Let us assume to the contrary that 5 – 4 \sqrt{7} is rational.
5 − 4 \sqrt{7} can be expressed as \frac{a}{b}where b ≠ 0 and a and b are coprime integers
5 − 4 \sqrt{7} = \frac{a}{b}
5 − \frac{a}{b} = 4 \sqrt{7}
5b − \frac{a}{b} = 4 \sqrt{7}
5b − \frac{a}{4b} = \sqrt{7}
Now 5b − \frac{a}{4b} is a rational number since 4 , 5 , a and b are integers
\sqrt{7} will also be rational but this contradicts the fact that \sqrt{7} is irrational
Our assumption that 5 − 4 \sqrt{7} is rational is wrong
5 − 4 \sqrt{7} is irrational.
(D) If two zeros of the polynomial 3x4 − 10x3 − 17x2 + 30x + 24 are \sqrt{3} and − \sqrt{3} , then find the other two zeros.
Ans : Since the two zeros are \sqrt{3} and − \sqrt{3}
( x − \sqrt{3}) ( x + \sqrt{3} ) = x2 − 3 is a factor of the given polynomial.
3x2 − 10x − 8 is another factor
Factorising this we get
3x2 − 10x − 8 = 0
3x2 − 12x + 2x − 8 = 0
3x ( x − 4) ( 3x + 2x ) = 0
( x − 4 ) ( 3x + 2) = 0
x − 4 = 0 Or 3x + 2 = 0
x = 4 Or x = − \frac{2}{3}
The other two zeros are 4 and − \frac{2}{3}
2 (A) Select and write the most appropriate alternative from those given below :
A box contains some discs which are numbered from 5 to 15. If one disc is drawn at random from the box, then the probability of getting a multiple of 3 or 4 is ____.
(a) \frac{6}{11}
(b) \frac{5}{11}
(c) \frac{3}{10}
(d) \frac{7}{10}
Ans : (b) \frac{5}{11}
(B) A die and a coin are thrown once simultaneously. Find the probability of getting:
1. A prime number and a head
2. A number greater than 4 and a tail.
Ans : When a die and coin are thrown once simultaneously the total possible outcomes are 12
1. To get a prime number and heads the favorable outcomes are 3
P(E) = \frac{Number \thinspace \thinspace of \thinspace \thinspace outcomes \thinspace \thinspace favourable }{Number \thinspace \thinspace of \thinspace \thinspace all \thinspace \thinspace possible \thinspace \thinspace outcomes}
P ( prime number and heads ) = \frac{3}{12}
= \frac{1}{4}
2. P(E) = \frac{Number \thinspace \thinspace of \thinspace \thinspace outcomes \thinspace \thinspace favourable }{Number \thinspace \thinspace of \thinspace all \thinspace \thinspace possible \thinspace \thinspace outcomes}
P ( number greater than 4 and a tail) = \frac{2}{12}
= \frac{1}{6}
(C) Find the roots of ANY ONE of the following quadratic equations :
1. 4x2 + 11x − 20 = 0
( By factorization method )
Ans: 4x2 + 11x − 20 = 0
4x2 + 16x − 5x − 20 = 0
4x ( x + 4) − 5 ( x + 4) = 0
( x + 4 ) ( 4x − 5) = 0
x + 4 = 0 Or 4x − 5 = 0
x = − 4 Or x = \frac{5}{4}
The roots are − 4 and \frac{5}{4}
2. 4x2 + 12x − 7 = 0
( By using quadratic formula)
Ans : 4x2 + 12x − 7 = 0
a = 4 b = 12 and c = − 7
b2 − 4ac = 122 − 4 × 4 × − 7
= 144 + 112
= 256
x = − b ± \frac{ \sqrt{ b^{2} - 4ac } }{2a }
= − 12 ± \frac{ \sqrt{256} }{2 × 4}
= − 12 + \frac{16}{8} OR − 12 − \frac{16}{8}
= \frac{4}{8} OR − \frac{28}{8}
The roots are \frac{1}{2} OR − \frac{7}{2}
(D) A group of students planned a picnic and estimated the expenditure to be Rs 5,000. Five more students joined the group so the expenditure was increased by Rs 1,000, but the average expenses per student was decreased by Rs 10. Find the total number of students who went for the picnic.
Ans : Let the total no of students be x
Total expenditure is Rs 5000
Average expenses = Rs \frac{5000}{x}
If 5 more students join, expenditure
= 5000 + 1000 = Rs 6000 and
Average expenses per student = \frac{6000}{x + 5}
By problem
\frac{6000}{x + 5} = \frac{5000}{x − 10}
6000x = 5000 ( x + 5) − 10x ( x + 5)
6000x = 5000x + 25000 − 10x2 − 50x
10x2 + 6000x − 5000x + 50x − 25000 = 0
10x2 + 1050x − 25000 = 0
x2 + 105x − 2500 = 0 ( Dividing by 10 )
x2 + 125x − 20x − 2500 = 0
x (x + 125) − 20 (x + 125) = 0
(x + 125) ( x − 20 )= 0
x + 125 = 0 OR x − 20 = 0
x = − 125 OR x = 20
− 125 is discarded
No of students who went for the picnic is 20
3(A) Select and write the most appropriate alternative from those given below :
A car takes ‘y’ hours to travel from city A to city B with a speed of ‘x’ km / hr, then the distance between the two cities can be written as ____ km.
(a) x + y
(b) \frac{x}{y}
(c) x , y
(d) \frac{y}{x}
Ans : (c) x , y
(B) The numerator of a fraction is greater than the denominator by 2. If 1 is added to the numerator the value of the fraction becomes 2.
Represent the above statements by two linear equations in x and y.
Ans : Let the numerator be x and denominator be y
The fraction is \frac{x}{y}
By problem : x = y + 2
x − y = 2 ….. eq (1)
x + \frac{1}{y} = 2
x + 1 = 2y
x − 2y = − 1 ….. eq (2)
The two equations are
x − y = 2 and x − 2y = − 1
(C) Find the solution of ANY ONE of the following linear equations :
1. 2x + 5y = − 4 and
3x − 2y = 13
( By elimination method )
Ans : 2x + 5y = − 4 ….. eq (1) …. × 2
3x – 2y = 13 ..… eq (2) ….. × 5
4x + 10 y = − 8
+ 15x − 10 y = 65
______________
19x = 57
x = \frac{57}{19}
x = 3
Substitute x = 3 in eq. (1)
2x + 5y = − 4
2 (3) + 5y = − 4
6 + 5y = − 4
5y = − 4 − 6
5y = − 10
y = − \frac{10}{5}
y = − 2
The solution is x = 3 and y = − 2
OR
2. 3x + 2y = 6
4x − 3y = 25
( By Cross multiplication method )
Ans : 3x + 2y − 6 = 0
4x − 3y − 25 = 0
a1 = 3 b1 = 2 c1 = − 6
a2 = 4 b2 = − 3 c2 = − 25
\frac{x}{ b_{1} c_{2} − b_{2} c_{1} } = \frac{y}{ c_{1} a_{2} − c_{2} a_{1} }
= \frac{1}{ a_{1} b_{2} - a_{2} b_{1} }
\frac{x}{2 ( -25) − (- 3) ( - 6)}
= \frac{y}{(-6) (4) − (−25) 3}
= \frac{1}{3 ( − 3) − 4 (2)}
\frac{x}{− 50 − 18}
= \frac{y}{− 24 + 75}
= \frac{1}{− 9 − 8}
\frac{x}{ − 68}
= \frac{y}{51}
= \frac{1}{− 17}
x = \frac{− 68}{ − 17} and y = \frac{51}{ − 17}
x = 4 and y = − 3
The solution is x = 4 andy = − 3
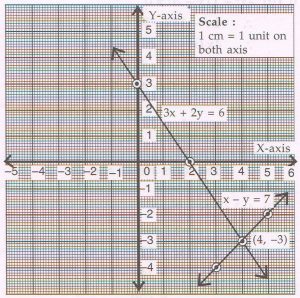
(D) Find the solution of the following pair of linear equations graphically :
x − y = 7 and 3x + 2y = 6
Rewrite and complete the following tables.
x − y = 7
|
x |
|
|
|
|
y |
|
|
|
3x + 2y = 6
|
x |
|
|
|
|
y |
|
|
|
( Plot at least 3 points for each line using a graph paper )
Ans : x − y = 7
|
x |
3 |
4 |
5 |
|
y |
− 4 |
−3 |
− 2 |
−
3x + 2y = 6
|
x |
2 |
4 |
0 |
|
y |
0 |
− 3 |
3 |
Solution is x = 4 , y = − 3
4(A) Select and write the most appropriate alternative from those given below :
The sum of the first ‘n’ terms of an A.P. whose first term is 8 and last term is 62, is 700. Therefore the A.P. consists of ____ terms.
(a) 15
(b) 20
(c) 25
(d) 30
Ans : (b) 20
(B) The following table shows the weight of 30 students of a class:
|
Weight (kg) |
No. of students |
|
35 − 40 |
5 |
|
40 − 45 |
7 |
|
45 − 50 |
11 |
|
50 − 55 |
7 |
Find the median of the above data up to two decimal places.
Ans :
|
Weight (kg) C.I |
No. of students f |
Cumulative Frequency Cf |
|
35 − 40 |
5 |
5 |
|
40 − 45 |
7 |
12 |
|
45 − 50 |
11 |
23 |
|
50 − 55 |
7 |
30 |
n = 30
\frac{n}{2} = 15
Median class is 45 – 50
l = 45
f = 11
Cf = 12
h = 5
Median = l + ( \frac{n}{2} − \frac{Cf}{f} ) × h
= 45 + ( 15 − \frac{12}{11} ) × 5
= 45 + \frac{3}{11} × 5
= 45 + \frac{15}{11}
= 45 + 1.36
= 46. 36
The Median is 45.36 kg
(C) A man started saving money from the first week of January 2017. He saved Rs 25 in the first week, Rs 40 in the second week, Rs 55 in the third week and so, till the last week of December 2017. Find the total saving of the man in the year 2017.
Ans : The period from 1st week of January 2017 to the last week of December 2017 includes 52 weeks.
n = 52, a = 25 , d = 40 − 25 = 15
Sn= \frac{n}{2} [ 2a + ( n − 1) d ]
Sn = \frac{52}{2} [ 2 × 25 + ( 52 − 1) 15 ]
Sn = 26 [ 50 + 51 × 15 ]
Sn = 26 [ 50 + 765 ]
= 26 × 815
= Rs 21,190
The man’s total saving in the year 2017 is Rs 21,190.
(D) The distribution given below shows the daily wages of the employees working in a factory:
Taking the classmark denoted by ‘a’ of the class interval ( 400 − 450) as the assumed mean, rewrite and complete the table and also find the mean of the daily wages by the assumed mean method.
Ans :
|
C.I |
fi |
xi |
di= xi− 425 |
fidi |
|
300 − 350 |
5 |
325 |
− 100 |
− 500 |
|
350 − 400 |
9 |
375 |
− 50 |
− 450 |
|
400 − 450 |
16 |
425 |
0 |
0 |
|
450 − 500 |
9 |
475 |
50 |
450 |
|
500 − 550 |
5 |
525 |
100 |
500 |
|
550 − 600 |
6 |
575 |
150 |
900 |
|
Total ∑fi = 50 |
|
|
|
∑fidi = 900 |
Mean = a + \frac{∑fidi}{∑fi}
= 425 + ( \frac{900}{50})
= 425 + 18
= 443
Mean of the daily wages is Rs 443.
5(A) Select and write the most appropriate alternative from those given below :
PA and PB are tangent segments drawn from external point ‘P’ to a circle with centre ‘O’ at A and B respectively. If ∠ AOB and ∠ APB are in the ratio 3 : 2 , then ∠ APO = _____°.
(a) 72
(b) 36
(c) 108
(d) 90
Ans : (b) 36
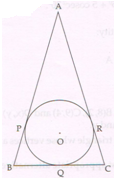
(B) Given: A circle with centre ‘O’ is inscribed in D ABC, where AB = AC. The sides AB, BC and AC touch the circle at points P, Q and R respectively.
Prove that : ‘Q’ is the mid-point of BC.
Proof : AP = AR ….. tangent segments from point A
BP = BQ ….. tangent segments from point B
CQ = CR ….. tangent segments from point C
AP + BP + CQ = AR + BQ + CR
AB + CQ = AR + CR + BQ
AB + CQ = AC + BQ
Since AB = AC ( given)
CQ = BQ
Q is the mid-point of BC
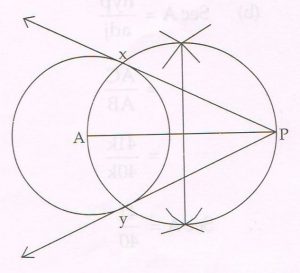
(C) Draw a circle with center ‘A’ and radius 3.5 cm. Then take a point ‘P’ at a distance of 8.5 cm from the center of the circle. Using a pair of compass and ruler, construct two tangent segments PX and PY to the circle. Measure and state the length of the tangent segments.
Ans :
Length of tangent segment Px = Py = 7.7 cm.
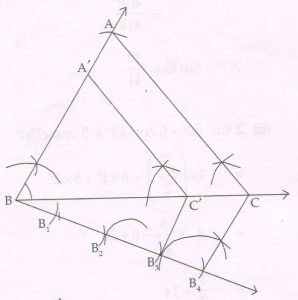
(D) Using a pair of compasses and ruler, construct Δ ABC with sides AB = 6.5 cm, BC = 7.2 cm and ∠ ABC = 60°. Then construct Δ A’BC’ whose sides are \frac{3}{4} of the corresponding sides of Δ ABC.
Ans:
6(A) Select and write the most appropriate alternative from those given below :
If 3 sin A − 4 Cos A = 0, then the value of Tan A = ____.
(a) \frac{7}{4}
(b) \frac{4}{7}
(c) \frac{4}{3}
(d) \frac{3}{4}
Ans : (c) \frac{4}{3}
(B) Attempt ANY ONE of the following :
1. In Δ ABC, if ∠ ABC = 90° and Tan A = \frac{9}{40},
Find:
(a) The length of AC
(b) The value of Sec A
(c) The value of Sin C.
Ans : Tan A = \frac{9}{40}
\frac{BC}{AB} = \frac{9}{40}
BC = 9k and AB = 40k
By Pythagoras theorem
AC2 = BC2 + AB2
AC2 = ( 9k)2 + ( 40k)2
= 81k2 + 1600k2
= 1681k2
AC = \sqrt{1681k²}
= 41 k
(a) Length of AC = 41k
(b) Sec A = \frac{hyp}{adj}
= \frac{AC}{AB}
= \frac{41k}{40k}
Sec A = \frac{41}{40}
(c) Sin C = \frac{AB}{AC}
= \frac{40k}{41k}
Sin C = \frac{40}{41}
2 Evaluate the following expression using known numerical values of trigonometric rations:
2 sin2 60° − 6 cot2 45° + 5 cosec2 30°.
Ans : 2 sin2 60° − 6 cot2 45° + 5 cosec2 30°.
= 2 × ( \frac{ \sqrt{3} }{2} )2 − 6 × 12 + 5 × 22
= 2 × \frac{3}{4} − 6 + 20
= \frac{3}{2} + 14
= \frac{ ( 2 + 28)}{2}
= \frac{31}{2}
(C) Prove the following identity :
\sqrt{ \frac{1 - sin A}{1 + sin A} } = sec A - tan A
Ans:
L.H.S. = \sqrt{ \frac{1 - sin A}{1 + sin A} }
= \sqrt{ \frac{(1 - sin A) ( 1 - sin A)}{(1 + sin A)( 1 - sin A)} }
= \sqrt{ \frac{(1 - sin A)² }{1 - sin² A} }
= \sqrt{ \frac{( 1 - sin A)²}{cos² A} }
= \frac{1 - sin A}{cos A}
= \frac{1}{cos A} − \frac{sin A}{cos A}
= sec A − tan A
(D) Attempt the following :
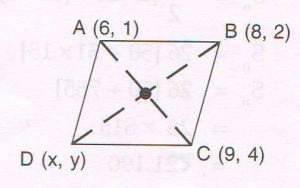
1. If the points A (6 , 1), B (8, 2) , C (9, 4 ) and D (x , y) are the vertices of a parallelogram, taken in order, find the value of x and y.
Ans:
Since ABCD is a parallelogram
Diagonals AC and BD bisect each other at point P (a , b)
P is the midpoint of AC and BD
P ( a , b) = \frac{ x_{1} + x_{2} }{2} , \frac{ y_{1} + y_{2} }{2}
a = 6 + \frac{9}{2}
b = 1 + \frac{4}{2} [ considering midpoint of AC]
a = \frac{15}{2} b = \frac{5}{2}
a = x + \frac{8}{2}
b = y + \frac{2}{2} [ considering midpoint of BC]
x + \frac{8}{2}= \frac{15}{2}
and y + \frac{2}{2} = \frac{5}{2}
x + 8 = 15 y + 2 = 5
x = 15 − 8 y = 5 − 2
x = 7 and y = 3
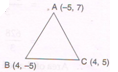
2. Find the area of the triangle whose vertices are A ( − 5, 7), B (4 , − 5) and C ( 4 , 5).
Ans : Area of Δ
= \frac{1}{2} [ x1 ( y2 − y3) + x2 ( y3 − y1) + x3 ( y1 − y2) ]
= \frac{1}{2} [− 5 (− 5 − 5) + 4 ( 5 − 7) + 4 ( 7 − ( − 5 )]
= \frac{1}{2} [− 5 (− 10) + 4 (− 2) + 4 (12) ]
= \frac{1}{2} [ 50 − 8 + 48 ]
= \frac{1}{2} [ 90 ]
= 45 sq. units
Area of the Δ is 45 sq. units
7(A) Select and write the most appropriate alternative from those given below :
In Δ ABC, points P and Q are on sides AB and AC respectively such that PQ \| BC . If A.P : PB = 1 : 2 and ar ( APQ) = 6 sq. units, then ar ( sq. PBCQ ) = ____ sq. units.
(a) 12
(b) 18
(c) 36
(d) 48
Ans : (d) 48
(B) With reference to the given figure and the given condition, write only the proof with reasons of the following theorem:
In Δ ABC, AB2 + BC2 = AC2 and Δ PQR is constructed such that PQ = AB, QR = BC and ∠ Q = 90°
Prove that :
Δ ABC is a right-angled triangle.
Proof :
In Δ ABC and ΔPQR
1) AB2 + BC2 = AC2 ….. given
2) PQ2 + QR2 = AC2 .…. AB = PQ and BC = QR
3) PQ2 + QR2 = PR2 Pythagoras theorem
4) AC2 = PR2 from step 2) and 3)
5) AC = PR
6) In Δ ABC and Δ PQR
AB = PQ by construction
BC = QR by construction
AC = PR step 5)
7) Δ ABC ≅ Δ PQR (S.S.S congruence rule)
8) ∠ B = ∠ Q (c.p.c.t)
9) ∠ B = 90° since ∠Q is 90°
10) ΔABC is a right-angled triangle
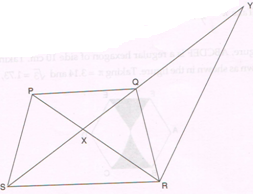
(C) Given: In PQRS, PQ \| SR, diagonals PR and QS intersect at X, a line through R parallel to PS intersect diagonal SQ on producing at Y. (S − Q −Y).
( \frac{PX}{RX})2 = \frac{QX}{XY}.
Proof: In Δ’s PXQ and RXS
1) ∠PQX = ∠XSR ….. alt. ∠s PQ \| SR
2) ∠QPX = ∠ XRS ….. alt. ∠s PQ \| SR
3) Δ PXQ ∼ ΔRXS A A similarity corollary
4) PX /RX = QX / XS ….. (c.p.c.t)
In Δ’s PXS and RXY
5) ∠PSX = ∠XYR ….. alt. ∠s PS \| RY
6) ∠SPX = ∠XRY ….. alt. ∠s PS \| RY
7) Δ PXS ∼ ΔRXY A A similarity corollary
8) \frac{PX}{RX} = \frac{XS}{XY} = \frac{PS}{RY} …..
(Corresponding. Sides. of Similar. Triangles)
9) (\frac{PX}{RX}) × (\frac{PX}{RX}) = (\frac{QX}{XS}) (\frac{XS}{XY}) ….. Multiplying step 4 and 8
10) ( \frac{PX}{RX})2 = (\frac{QX}{XS})(\frac{XS}{XY}) = \frac{QX}{XY}
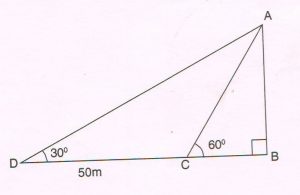
(D) The shadow of a tower AB, standing on a level ground is found to be 50 m longer when the sun’s altitude is 30° than when it is 60°. Find the height of the tower ( Take = 1.73 ).
Ans : Let AB = x and BC = y
In right Δ ABC
tan 60° = \frac{opp}{adj} = \frac{AB}{BC}
\sqrt{3} = \frac{x}{y}
x = y \sqrt{3} ….. (1)
In right Δ ABC
tan 30° = \frac{AB}{BD}
\frac{1}{ \sqrt{3} } = \frac{x}{50 + y}
x \sqrt{3} = 50 + y
y \sqrt{3} × \sqrt{3} = 50 + y ….. from (1)
3y = 50 + y
3y − y = 50
2y = 50
y = \frac{50}{2} = 25
x = 25 \sqrt{3} ….. (1)
x = 25 × 1.73
x = 43.25
Height of the tower is 43.25 m
8 (A) Select and write the most appropriate alternative from those given below :
1. If the area of a circle is numerically equal to twice the circumference then its radius is ____ cm.
(a) 16
(b) 8
(c) 4
(d) 2
Ans : (c) 4
2. The total surface area of a right circular cylinder with a radius of its base 3 cm and height of 2 cm is ____ sq. cm.
(a) 15 π
(b) 30 π
(c) 18 π
(d) 36 π
Ans : (b) 30 π
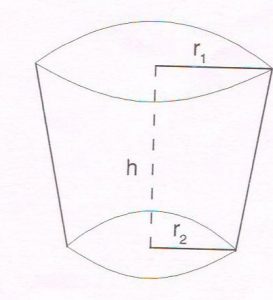
(B) A container, open at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 21 cm, with radii of its lower and upper ends 6 cm and 10 cm respectively. Find the volume of the container
( Take π = \frac{22}{7} )
Ans :
h = 21 cm
r2 = 6 cm
r1 = 10 cm
volume = ?
Volume of frustum = \frac{1}{3} π h ( r21 + r22 + r1. r2 )
= 1/3 22/7 21 ( 102 + 62 + 10 6 )
= 22 ( 100 + 36 + 60 )
= 22 × 16
= 4312
Volume of container is 4312 cm3
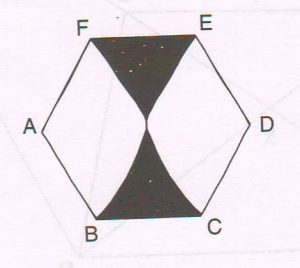
(C) In the figure, ABCDEF is a regular hexagon of side 10 cm. taking AB and DE as radii two sectors are drawn as shown in the figure. Taking π = 3.14 and = 1.73, find the area of the shaded region.
Ans : ABCDEF is a regular hexagon
Each angle of the hexagon is 120°
Area of hexagon =3 \frac{ \sqrt{3} }{ 3 } side2
= 3 × \frac{1.73}{2} × 10 × 10
= 150 × 1.73
= 259.5 cm2
Area of 2 sectors = 2 × \frac{Ø}{360} × πr2
= 2 × \frac{120}{360} × 3.14 × 10 × 10
= 2 × \frac{314}{3}
= \frac{628}{3}
= 209.3 cm2
Area of shaded region = Area of the hexagon − Area of 2 sectors
= 259.5 − 209.3
= 50.2 cm2 (approx)
(D) A metallic ball of a radius 10.5 cm is melted and recast into 126 cones of equal size. If the height of the cones formed is 3 cm, then find the radius of each cone ( Take π = \frac{22}{7} ).
Ans : Radius of ball ( sphere) → R = 10.5 cm
Height of cone → h = 3 cm
Number of cones → 126
Radius of cone → r = ?
126 × Volume of cone = Volume of ball
126 × \frac{1}{3} πr2 h = \frac{4}{3} π R3
126 × \frac{1}{3} × r2 × 3 = \frac{4}{3} × 10.5 × 10.5 × 10.5
r2 = 4 × 3.5 × 10.5 × \frac{10.5}{126}
r2 = 2 × 0.5 × 3.5 × 3.5
= 1 × ( 3.5 )2
r2 = ( 3.5 )2
r = 3.5 cm
Radius of each cone is 3.5 cm