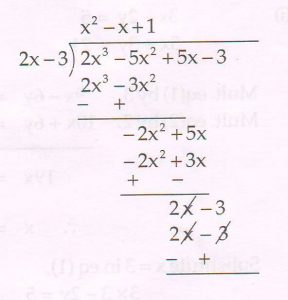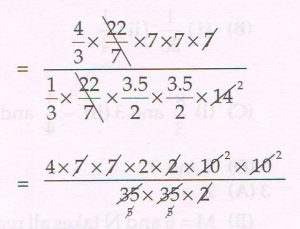Goa Board Paper MARCH 2019
1(A) Select and write the most appropriate alternative from those given below :
The product of two numbers is 846. If their HCF is 12, then their LCM is _____.
(a) 12
(b) 72
(c) 852
(d) 876
Ans : (b) 72
(B) Attempt the following :
1. Find the sum of zeroes of the quadratic polynomial 2x2 − 7x − 15.
Ans : The sum of the zeros = − \frac{b}{a}
= − \frac{( − 7)}{2}
= \frac{7}{2}
2. Find the zeroes of the quadratic polynomial x2 − 11x.
Ans : To obtain zeros, x2 − 11x = 0
x ( x − 11) = 0
Either x = 0 or x = 11
The zeros are 0 and 11.
(C) On dividing the polynomial 2x3 − 5x2 + 8x − 5 by a polynomial g (x), the quotient and the remainder are ( 2x − 3) and (3x − 2) respectively. Find g (x).
Ans : Dividend = Divisor × Quotient + Remainder
2x3 − 5x2 + 8x − 5 = g (x) ( 2x − 3) + ( 3x − 2)
2x3 − 5x2 + 8x − 5 \frac{− 3x + 2}{2x − 3} = g (x)
g (x) = ( 2x3 − 5x2 + 5x − 3 ) ÷ ( 2x − 3)
g (x) = x2 − x + 1
(D) Prove that \sqrt{7} is an irrational number.
Proof : let us assume, to the contrary, that \sqrt{7} is rational.
So, we can find integers a and b coprime, such that
\sqrt{7} = \frac{a}{b}
a = b \sqrt{7}
a2 = 7b2(squaring both sides )
Therefore 7 divides a2
7 divides a ( by a theorem) …… (1)
a = 7c where c is some integer
a2 = 49 c2
Substituting 7b2 = 49c2
b2 = 7c
7 divides b2
7 divides b ….. (2)
From (1) and (2) a and b have 7 as a common factor
But this contradicts our assumption that a and b are coprime
Our assumption that \sqrt{7} is rational is incorrect.
Thus we conclude that \sqrt{7} is rational.
2(A) Select and write the most appropriate alternative from those given below :
If P (E) = 0.07, then the probability of getting an event “not E” is ____.
(a) 0.03
(b) 0.93
(c) 1.00
(d) 1.07
Ans : (a) 0.03
(B) A card is drawn from a well-shuffled deck of 52 playing cards. Find the probability of getting :
1. An ace
2. A red face card.
Ans : 1. Let E be the event of getting an ace
P (E) = \frac{No. \thinspace of \thinspace outcomes \thinspace favourable\thinspace \thinspace to \thinspace E}{No.\thinspace of\thinspace all \thinspace possible \thinspace outcomes}
= \frac{4}{52}
= \frac{1}{13}
2. Let F be the event of getting a red face card
P (F) = \frac{No. \thinspace of \thinspace outcomes \thinspace favourable\thinspace \thinspace to \thinspace E}{No.\thinspace of\thinspace all \thinspace possible \thinspace outcomes}
= \frac{26}{52}
= \frac{1}{2}
(C) Find the roots of ANY ONE of the following quadratic equations :
1. 7x2 − 17x + 6 = 0
( By factorization method)
Ans : 7x2 − 17x + 6 = 0
7x2 − 14x − 3x + 6 = 0
7x ( x − 2) − 3 ( x − 2) = 0
(x − 2) ( 7x − 3) = 0
x − 2 = 0 or 7x − 3 = 0
x = 2 or x = \frac{3}{7}
Roots of the equations are 2 and \frac{3}{7}.
2. 3x2 + 10x − 8 = 0
( By quadratic formula method)
Ans : 3x2 + 10x − 8 = 0
a = 3 , b = 10 , c = − 8
b2 − 4ac = 102 − 4 × 3 ( − 8)
= 100 + 96
= 196
Roots are = − b ± \frac{ \sqrt{b² - 4ac } }{2a}
= − 10 \frac{ \sqrt{196 } }{2 × 3}
i.e., − 10 + \frac{14}{6} and − 10 \frac{ − 14}{6}
i.e., \frac{4}{6} and − \frac{24}{6}
Roots are = \frac{2}{3} and − 4
(D) Two pipes A and B running together can fill a tank in 3 \frac{1}{3} minutes. If pipes B takes 5 minutes more than pipe A to fill the tank separately, then find the time in which each pipe would fill the tank separately.
Ans : Let the time taken by pipe A to fill the tank separately be x minutes.
The time taken by pipe B to fill the tank separately is ( x + 5) minutes.
In one-minute pipe A can fill the tank \frac{1}{x}
And in one minute pipe B can fill the tank \frac{1}{x + 5}
Pipe A and B fill the tank 1 \frac{1}{ \frac{x +1}{x +5} } in one minute.
But the two pipes together fill the tank in 3 \frac{1}{3} = \frac{10}{3} minutes
The two pipes together fill the tank in one minute = \frac{3}{10}
\frac{1}{x} + \frac{1}{x} + 5 = \frac{3}{10}
10 (x + 5) + 10x = 3x ( x + 5)
10x + 50 + 10x = 3x2 + 15x
20x + 50 = 3x2 + 15x
3x2 − 5x − 50 = 0
3x2 − 15x + 10x − 50 = 0
3x ( x − 5) + 10 ( x − 5) = 0
( x − 5) ( 3x + 10 ) = 0
x −5 = 0 or 3x + 10 = 0
x = 5 or x = − \frac{10}{3}
− \frac{10}{3} being in negative, is not to be taken
x = 5 will be the answer
Pipe A takes 5 minutes to fill the tank separately.
And pipe B takes 5 + 5 = 10 minutes to fill the tank separately.
3(A) Select and write the most appropriate alternative from those given below :
Three years hence, the ages of two friends will be x and y years respectively. Therefore the sum of their ages two years ago was ____ years.
(a) x + y + 10
(b) x + y + 5
(c) x + y − 10
(d) x + y − 5
Ans : (c) x + y − 10
(B) The following is a pair of linear equations in two variables :
2x + 3y = 7
( k + 1) x + (2k − 1) y = 4k + 1.
Answer the following questions with reference to the given pair of equations:
1. Write down the condition for infinitely many solutions.
2. Find the value of k.
Ans : 2x + 3y − 7 = 0
( k + 1 ) x + ( 2k − 1) y − ( 4k + 1) = 0
1. For infinitely many solutions the condition is
\frac{2}{k + 1} = \frac{3}{2k − 1} = \frac{− 7}{− ( 4k + 1)}
2. To get the value of k,
\frac{2}{k + 1} = \frac{3}{2k − 1}
2 (2k − 1) = 3 ( k + 1)
4k − 2 = 3k + 3
4k − 3 k = 3 + 2
k = 5
(C) Find the solution of ANY ONE of the following pairs of linear equations :
1. 3x − 2y = 5 and
5x + 3y = 21
( By elimination method )
Ans : 3x − 2y = 5 …. (1)
5x + 3y = 21 …. (2)
Multiply. eq (1) by 3, 9x − 6y = 15
Multiply. eq (2) by 2, 10x + 6y = 42
_______________
19x = 57
x = \frac{57}{19}
x = 3
Substitute x = 3 in eq (1),
3 × 3 − 2y = 5
− 2y = 5 − 9
− 2y = − 4
y = 2
Solution is x = 3 , y = 2
2. 2x + 5y = 29
7x − 2y = 4
( By cross -multiplication method)
Ans : 2x + 5y − 29 = 0 ….. (1)
7x − 2y − 4 = 0 ….. (2)
\frac{x}{5 ( − 4) − (− 2) ( − 29)}
= \frac{y}{( − 29) 7 − 2 ( − 4)}
= \frac{1}{2 ( −) − 7 × 5} \frac{x}{− 20 − 58}
= \frac{y}{− 203 + 8}
= \frac{1}{− 4 − 35} \frac{x}{− 78}
= \frac{y}{− 195}
= \frac{1}{− 39}
\frac{x}{− 78} = \frac{1}{− 39}
x = \frac{− 78}{− 39} = 2
And \frac{y}{− 195} = \frac{1}{− 39}
y = \frac{− 195}{− 39} = 5
The solution is x = 2 ,y = 5
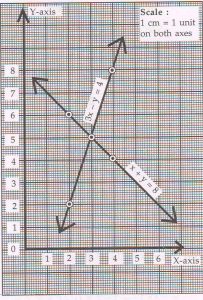
(D) Find the solution of the following pair of linear equations graphically:
x + y = 8 and
3x − y = 4
Rewrite and complete the following tables:
x + y = 8
|
x |
|
|
|
|
y |
|
|
|
3x − y = 4
|
x |
|
|
|
|
y |
|
|
|
( Plot at least 3 points for each line using a graph paper)
Ans :
x + y = 8
|
x |
2 |
3 |
4 |
|
y |
6 |
5 |
4 |
3x − y = 4
|
x |
2 |
3 |
4 |
|
y |
2 |
5 |
8 |
The graphical solution is x = 3, y = 5.
4 (A) Select and write the most appropriate alternative from those given below :
The sum of the first 20 odd natural numbers is ___.
(a) 100
(b) 210
(c) 400
(d) 420
Ans : (c) 400
(B) The following table shows the ages of 50 people in a locality:
|
Ages in Years |
Number of People |
|
5 − 15 |
10 |
|
15 − 25 |
12 |
|
25 − 35 |
15 |
|
35 − 45 |
13 |
Find the Median of the above given data.
Ans : In the distribution, n = 50 \frac{n}{2}= 25
Median class is 25 − 35.
Now Median = l + ( \frac{n}{2} − \frac{Cf}{f} ) × h
Where, l = lower limit of median class = 25
Cf = cumulative frequency of class preceding the median class
= 10 + 12 = 22
f = frequency of median class = 15
h = class size = 10
Median = 25 + ( 25 − \frac{22}{15}) × 10
= 25 + ( \frac{3}{15} ) × 10
= 25 + 2
= 27
(C) A factory manufacturing electric bulbs increases the production uniformly by a fixed number every month. If in the third month the production is 600 electric bulbs and in the seventh month the production is 800 electric bulbs, then find the total production of electric bulbs in the year.
Ans : an = a + ( n − 1) d
Now a3 = 600 = a + ( 3 − 1) d
a + 2d = 600 ….. (1)
And a7 = 800 = a + ( 7 − 1) d
a + 6d = 800 ….. (2)
Eq (2) − Eq (1),we get 4d = 200
d = \frac{200}{4}
d = 50
From (1), a + 2 × 50 = 600
a = 600 − 100
a = 500
S = \frac{n}{2} [ 2a + ( n − 1) d ] where n = 12 months
= \frac{12}{2} [ 2 × 500 + ( 12 − 1) × 50 ]
= 6 × [ 1000 + 11 × 50 ]
= 6 × [1000 + 550 ]
= 6 × 1550
= 9300
Total production of bulbs in the year = 9300
(D) The following table shows the donation collected by a club from 60 donors:
Taking the classmark denoted by ‘a’ of the class interval ( 40 − 60) as the assumed mean, rewrite and complete the table. Also, find the mean of the donation by the assumed mean method.
Ans : Assumed Mean a = 50
|
C.I |
fi |
xi |
di = xi − 50 |
fi di |
|
0 − 20 |
5 |
10 |
− 40 |
− 200 |
|
20− 40 |
12 |
30 |
− 20 |
− 240 |
|
40− 60 |
14 |
50 |
0 |
0 |
|
60 − 80 |
15 |
70 |
20 |
300 |
|
80 − 100 |
8 |
90 |
40 |
320 |
|
100 − 120 |
6 |
110 |
60 |
360 |
|
Total |
∑fi = 60 |
|
|
∑fi × di = 540 |
x = a + \frac{∑fidi}{∑fi}
= 50 + \frac{540}{60}
= 50 + 9
Mean = 59
5(A) Select and write the most appropriate alternative from those given below :
TP and TQ are tangents drawn from an external point T to a circle with centre O, at P and Q respectively. If ∠ POQ = 130°, then the measure of ∠ PTO = _____.
(a) 25°
(b) 50°
(c) 65°
(d) 130°
Ans : (a) 25°
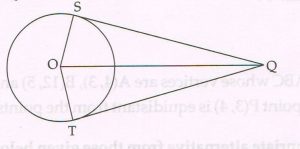
(B) Given: Point O is the centre. QS and QT are two tangent segments drawn from an external point Q to the circle at S and T respectively.
Prove that : QS = QT
( Write only the proof with reasons )
Proof : The two tangent segment QS and QT drawn from an external point Q to the circle at S and T respectively are at right angles to the respective radii OS and OT.
∠OSQ = 90° and ∠OTQ = 90°
Δ OSQ and Δ OTQ are right triangles
Now OS = OT ( radii of the same circle)
OQ = OQ ( common side)
Δ OSQ ≅ D OTQ ( hypotenuse-side theorem)
QS = QT ( c.p.c.t)
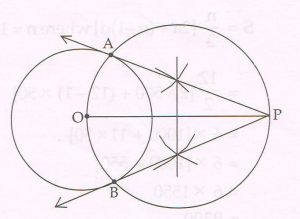
(C) Draw a circle with centre O and radius 3.5 cm. Take a point P at a distance of 8 cm from the centre of the circle. Using a pair of compasses and a ruler construct two tangents PA and PB to the circle. Measure and state the length of the tangent segments.
Ans :
The length of each tangent segment is 7.2 cm.
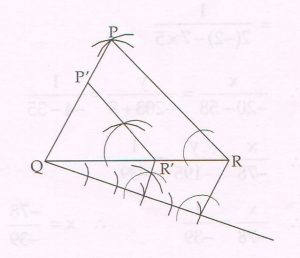
( D) Using a pair of compass and ruler construct Δ PQR with sides PQ = 7 cm, QR = 8.5 cm and PR = 6.5 cm. Then construct Δ P ‘QR’ whose sides are \frac{3}{5} of the corresponding sides of Δ PQR.
Ans :
P‘QR’ is the required triangle.
6 (A) Select and write the most appropriate alternative from those given below :
If cosec 3A = sec ( A − 22 ) where 3A is an acute angle, then the measure ∠A = _____’
(a) 11°
(b) 17°
(c) 28°
(d) 58°
Ans : (c) 28°
(B) Attempt ANY ONE of the following :
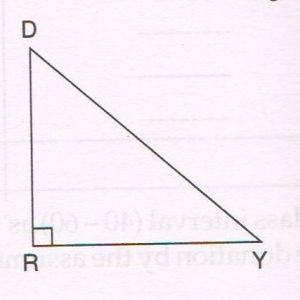
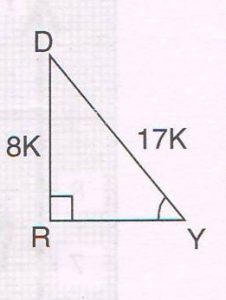
1. In ΔDRY, ∠ R = 90° and cosec Y = \frac{17}{8} :
Find :
(a) The length of YR
(b) The value of cot D
(c) The value of cos Y
Ans : (a) cosec Y = \frac{17}{8} sin Y = \frac{8}{17}
Let DR = 8k and DY = 17k
By Pythagoras theorem,
YR2 + DR2 = DY2
YR2 + ( 8k)2 = ( 17k)2
YR2 = 289k2 − 64k2
YR2 = 225 k2
YR = 15 k
(b) cot D = \frac{DR}{RY} = \frac{8k}{15k} = \frac{8}{15}
(c) cos Y = \frac{RY}{DY} = \frac{15k}{17k} = \frac{15}{17}
2. Evaluate the following expression using known numerical values of trigonometric ratios :
3 tan2 30° − 2 sec2 45° + \frac{1}{3} cos 60°.
Ans : 3 tan2 30° − 2 sec2 45° + \frac{1}{3} cos 60°
= 3 × ( \frac{1}{ \sqrt{3} } )2 − 2 × ( \sqrt{2} )2 + \frac{1}{3} × \frac{1}{2}
= 3 × \frac{1}{3} − 2 × 2 + \frac{1}{6}
= 1 − 4 + \frac{1}{6}
= − 3 + \frac{1}{6}
= − 18 + \frac{1}{6}
= − \frac{17}{6}
(C) Prove the following identity :
tan Ø + \frac{sec Ø - 1}{tan Ø − sec Ø} + 1 = sec Ø + tan Ø .
Ans :
L.H.S. = \frac{ \frac{sinØ }{cos Ø} + \frac{1}{cosØ} - 1 }{ \frac{sinØ}{cos Ø} - \frac{1}{cosØ} + 1}
= \frac{sinØ - cosØ + 1}{sinØ + cosØ - 1}
= \frac{(sinØ - cosØ + 1) ( sin Ø + cos Ø + 1 )}{(sinØ + cosØ - 1) ( sinØ + cos Ø + 1)}
= \frac{( sinØ + 1)² − ( cos Ø)²}{( sinØ + cosØ)² - 1²}
= \frac{sin²Ø + 2 sin Ø + 1 − cos²Ø }{sin²Ø + 2 sin Ø cosØ + cos² Ø −1}
= \frac{sin²Ø + 2 sin Ø + sin² Ø }{1 + 2 sin Ø cos Ø - 1}
= \frac{ 2 sin²Ø + 2 sin Ø }{ 2 sinØ cosØ }
= \frac{ 2 sin² Ø }{ 2 sinØ cosØ } + \frac{2 sinØ }{ 2 sinØ cosØ }
= \frac{sinØ}{ cosØ} + \frac{ 1}{cosØ }
= tan Ø + sec Ø
= R.H.S.
(D) Attempt the following :
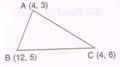
1. Find the area of triangle ABC whose vertices are A ( 4 , 3), B ( 12 , 5) and C ( 4 , 6).
Ans : Area of triangle
= \frac{1}{2} [ 4 ( 5 − 6) + 12 ( 6 − 3) + 4 ( 3 − 5) ]
= \frac{1}{2} [ 4 × ( − 1) + 12 × 3 + 4 ( − 2) ]
= \frac{1}{2} [ − 4 + 36 − 8 ]
= \frac{1}{2} × 24
= 12 square units.
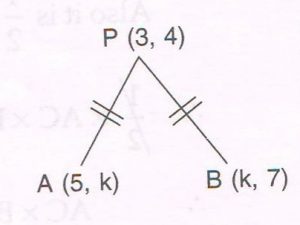
2. Find the value of k, if the point P ( 3 , 4) is equilateral from the points A ( 5, k) and B ( k , 7)
Ans : PA = PB
PA2 = PB2
( 3 − 5)2+ ( 4 − k)2 = ( 3 − k)2 + ( 4 − 7)2
4 + 16 − 8k + k2 = 9 − 6k + k2 + 9
20 − 8k = 18 − 6k
− 8k + 6k = 18 − 20
− 2k = − 2
k = \frac{− 2}{ − 2}
= 1
Value of k is 1
7 (A) Select and write the most appropriate alternative from those given below :
In Δ ABC, points D and E are on the sides of BC and AC respectively such that B − D − C , A − E − C and DE \| AB . If CE = 4 cm, AE = 5 cm and BD = 4.5 cm, then BC = _____ cm
(a) 3.6
(b) 5.6
(c) 8.1
(d) 9
Ans : (c) 8.1 cm
(B) With reference to the given figure and the given conditions, write only the proof with reasons of the following theorem.
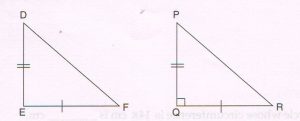
Given : In Δ DEF, DE2 + EF2 = DF2, Δ PQR is constructed such that PQ = DE , QR = EF and ∠ Q = 90°.
Prove that : Δ DEF is a right-angled triangle.
Proof : From Δ PQR,
PR2 = PQ2 + QR2( By Pythagoras theorem)
= DE2 + EF2 ( by given condition )
But DF2 = DE2 + EF2
PR = DF ….. (1)
In Δ DEF and Δ PQR
DE = PQ ( given)
EF = QR ( given)
DF = PR ( proved in (1) )
Δ DEF ≅ ΔPQR ( SSS congruence)
∠ E = ∠ Q ( c.p.c.t)
But ∠ Q = 90° ( given )
∠ E = 90°
ΔDEF is a right angled triangle.
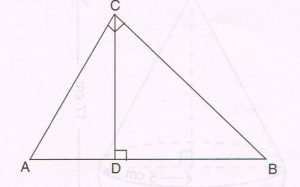
(C) Given : ΔABC is a right – angled triangle, right angled at C. Line segment CD is drawn perpendicular to side AB of Δ ABC.
Prove that : \frac{1}{CD²} = \frac{1}{BC²} = \frac{1}{AC²}
( Write only the proof with reasons).
Proof : Area of triangle = \frac{1}{2} × base × height
Area of Δ ABC = \frac{1}{2} × AC × BC
Also it is \frac{1}{2} × AB × CD
\frac{1}{2} × AC × BC = \frac{1}{2} × AB × CD ….. (1)
Now AB2 = AC2 + BC2( By Pythagoras theorem)
Dividing by (1), \frac{AB²}{AB²} × CD2 = \frac{AC²}{AC²} × BC2 + \frac{BC²}{AC²} × BC2
\frac{1}{CD²} = \frac{1}{BC²} + \frac{1}{AC²}
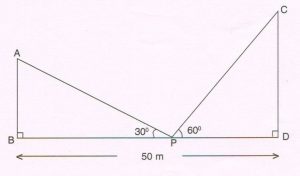
(D) Two pillars AB and CD are 50 m apart and the height of pillar CD is double the height of pillar AB as shown in the figure. From a point P on the line joining the feet of the pillars, an observer observes the top A of the pillar AB and top C of the pillar CD at angles of elevation 30° and 60° respectively. Find the height of the pillar AB and pillar CD.
( Take \sqrt{3} = 1.7 )
Ans : Let AB = x CD = 2x
Let BP = y PD = 50 − y
In Δ ABP, tan 30° = \frac{AB}{BP}
\frac{1}{ \sqrt{3} } = \frac{x}{y}
x = y \sqrt{3} ….. (1)
In ΔCDP, tan 60° = \frac{CD}{PD}
\sqrt{3} = \frac{2x}{50 − y}
2x = \sqrt{3} ( 50 − y )
From (1) and (2), 2 y = ( 50 − y)
2 \sqrt{3} y = 50 \sqrt{3} − \sqrt{3} y
50 \sqrt{3} = 3 \sqrt{3} y
y = \frac{50}{3}
From (1) , x = \frac{50}{3} × \sqrt{3} = 50 × \frac{1.73}{3} = \frac{85}{3} = 28.33
2x = 2 × 28.33
= 56.66
AB = 28.33 m and CD = 56.66 m
8 (A) Select and write the most appropriate alternative from those given below :
1. The length of an arc of a circle of radius 15 cm and subtending an angle 36° at the centre of the circle is _____ CM.
(a) 3 π
(b) 5 π
(c) 15 π
(d) 30 π
Ans : (a) 3 π
2. The diameter of a circle whose circumference is 14 π cm is ____ cm.
(a) 7
(b) 14
(c) 21
(d) 28
Ans : (b) 14
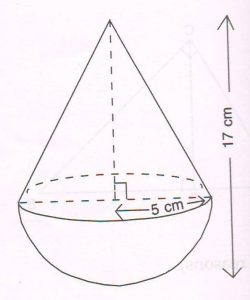
(B) A toy is in the form of a hemisphere surmounted by a conical top of the same base radius as shown in the figure. If the radius of the base of the conical top is 5 cm and the height of the toy is 17 cm,
Find :
1. The slant height of the cone.
Ans : Perpendicular height of the conical top
= ( 17 − 5 ) cm
= 12 cm
We know that l2 = r2 + h2
Let l be the slant height of the cone
Then l2 = 52 + 122( By Pythagoras theorem)
= 25 + 144
= 169
l = \sqrt{169} = 13 cm
Slant height is 13 cm.
2. The curved surface area of the hemisphere.
( Do not substitute for π )
Ans : Curved surface area of the hemisphere
= 2 π r2
= 2 π × 5 × 5 cm2
= 50 π cm2
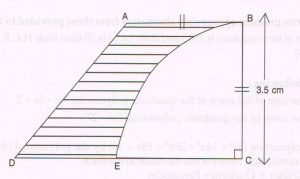
(C) In the adjoining figure a piece of cardboard is in the shape of a trapezium ABCD where AB \| DC and ∠BCD = 90°. A quadrant with centre C and radius 3.5 cm is drawn. If AB = BC and DE = 2 cm, then find the area of the shaded region.
( Take π = \frac{22}{7} )
Ans : Area of the quadrant = \frac{1}{4} π r2
= \frac{1}{4} × \frac{22}{7} × \frac{35}{10} × \frac{35}{10}
= 11 × \frac{35}{4} × 10 = \frac{96.25}{10}
= 9.625 cm2
Area of the trapezium = \frac{1}{2} [ AB + DC] × BC
= \frac{1}{2} [ 3.5 + 5.5 ] × 3.5
= 9 × \frac{3.5}{2}
= 15.75 square cm.
Area of the shaded region = ( 15.75 − 9.625) sq. cm
= ( 6. 125 cm2)
(D) The surface area of a solid metallic sphere is 616 cm2. The sphere is melted and recast into smaller cones, each of diameter 3.5 cm and height 14 cm respectively. Find the number of such cones formed.
( Take π = \frac{22}{7} )
Ans : 4 π r2 = 616
4 × \frac{22}{7} × r2 = 616 r2= 616 × \frac{7}{( 4 × 22)} = 72
r = 7
Volume of the sphere = \frac{4}{3} π r2
= \frac{4}{3} × \frac{22}{7} × 73 cm3 ….. (1)
Volume of each cone = \frac{1}{3} π R2 h
= \frac{1}{3} × \frac{22}{7} × \frac{3.5}{2} × \frac{3.5}{2} × 14 cm3 ….. (2)
Number of cones formed
= 4 × 8
= 32
Number of cones formed = 32