EXERCISE 2.2

                                                                EXERCISE 2.2

1) Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x
(iv) 4u² + 8u
(v) t² −15
(vi) 3x² – x – 4
Solution:

2) Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.

(i) 1/4, −1      (ii) √2, 1/3   (iii) 0,√5      (iv) 1,1        (v) −1/4, 1/4        (vi) 4, 1.

Solution:
(i) Zeroes of polynomial are not given,   sum of zeroes = 1/4 and product of zeroes = −1
If ax² + bx + c is a quadratic polynomial, then
α + β = sum of zeroes = −b/a = 1/4 and αβ = product of zeroes = c/a = −1
Quadratic polynomial is  ax² + bx + c
Let a = k,   ∴ b = −k/4   and c = −k
Putting these values, we get

For different real values of k, we can have quadratic polynomials all having sum of zeroes as 14 and product of zeroes as −1.

(ii) Sum of zeroes = α + β = √2 = −b/a;    product of zeroes = αβ = 1/3 = c/a
Quadratic polynomial is ax² + bx + c
Let a = k,   b = −√2/k   and   c = k/3
Putting these values we get

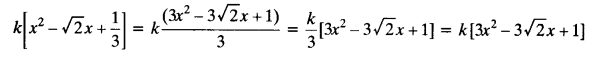
For all different real values of k, we can have different quadratic polynomials of the form 3x² – 3√2x +1 having sum of zeroes = √2 and product of zeroes =1/3

(iii) Sum of zeroes = α + β = 0 = −b/a;   product of zeroes = αβ = √5 = c/a
Let quadratic polynomial is ax² + bx + c
Let a = k, b = 0,  c = √5 k
Putting these values, we get
k [x² – 0x + √5 ] = k (x² + √5).
For different real values of k, we can have different quadratic polynomials of the form
x² + √5, having sum of zeroes = 0 and product of zeroes = √5

(iv) Sum of zeroes = α + β = 1= −b/a;   product of zeroes = αβ = 1 = c/a
Let quadratic polynomial is ax² + bx + c.
Let a = k,   c = k,   b = −k
Putting these values, we get k [x² −x +1]
Quadratic polynomial is of the form x² −x + 1 for different values of k.

(v) Sum of zeroes = α + β = −1/4 = −b/a;    product of zeroes = αβ = 1/4 = c/a
Let quadratic polynomial is ax² + bx + c
Let a= k,   b = k/4,   c = k/4
Putting these values, we get k

Quadratic polynomial is of the form 4x² +x + 1 for different values of k.

(vi) Sum of zeroes = α + β = 4 = −b/a;   product of zeroes = αβ = 1 = c/a
Let quadratic polynomial is ax² + bx + c
Let a = k,  b = −4/k and c = k
Putting these values, we get
k [x² – 4x + 1]
Quadratic polynomial is of the form x² – 4x + 1 for different values of k.