EXERCISE 2.3

                                                                          EXERCISE 2.3

1) Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder, in each of the following:
(i) p(x) = x³ – 3x² + 5x −3,     g(x) = x² −2 
(ii) p(x) = x⁴ – 3x² + 4x + 5,   g(x) = x² + 1 −x
(iii) p(x) = x⁴ – 5x + 6,             g(x) = 2 −x²
Solution:
(i) Here p(x) = x³ −3x² + 5x – 3 and g(x) = x² −2
Dividing p(x) by g(x) ⇒

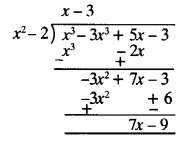
Quotient = x – 3, Remainder = 7x – 9

(ii) Here p(x) = x⁴– 3x² + 4x + 5 and g(x) = x² + 1 −x
Dividing p(x) by g(x) ⇒

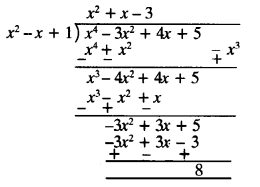
Quotient = x² + x – 3, Remainder = 8

(iii) Here   p(x) = x⁴– 5x + 6 and g(x) = 2−x²
Rearranging g(x) = −x² + 2
Dividing p(x) by g(x) ⇒
Quotient = −x² – 2
Remainder = −5x + 10.

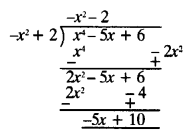
2) Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t²−3,  2t⁴ + t³ – 2t² – 9t – 12
(ii) x² + 3x + 1,  3x⁴+5x³−7x² + 2x + 2
(iii) x³ −3x + 1,   x⁵ – 4x³ + x² + 3x + l
Solution:
(i) First polynomial = t² – 3,
Second polynomial = 2t⁴ + 3t³ – 2t² – 9t – 12
Dividing second polynomial by first polynomial 
∵ Remainder is zero.
∴ First polynomial is a factor of second polynomial.

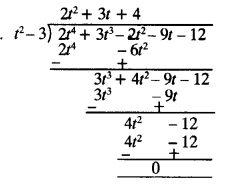
(ii) First polynomial = x² + 3x + 1
Second polynomial = 3x⁴ + 5x³ – 7x² + 2x + 2
Dividing second polynomial by first polynomial 
∵ Remainder is zero.
∴ First polynomial is a factor of second polynomial.

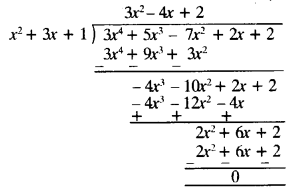
(iii) First polynomial = x³ – 3x + 1
Second polynomial = x⁵ – 4x³ + x² + 3x + 1.
Dividing second polynomial by first polynomial 
∵ Remainder ≠ 0.
∴ First polynomial is not a factor of second polynomial.

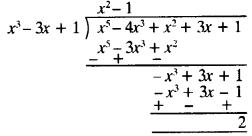
3) Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are √5/3 and –√5/3
Solution:

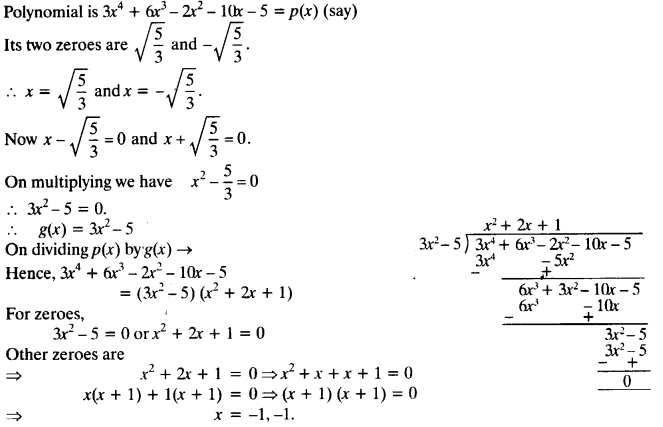
4) On dividing x³ – 3x² + x + 2  by a polynomial g(x), the quotient and remainder
were x – 2 and  −2x + 4, respectively. Find g(x).
Solution:
p(x) = x³ – 3x² + x + 2 ,    g(x) = ?
Quotient = x – 2; Remainder = −2x + 4
On dividing p(x) by g(x), we have
p(x) = g(x) x quotient + remainder
⇒ x³– 3x² + x + 2 = g(x) (x – 2) + (−2x + 4)
⇒ x³ – 3x² + x + 2 + 2 x −4 = g(x) x (x−2)
⇒ x³ – 3x² + 3x – 2 = g(x) (x – 2)

5) Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
(i) p(x),   g(x),   q(x),   r(x)
deg p(x) = deg q(x)
∴ both g(x) and r(x) are constant terms.
p(x) = 2x²– 2x + 14;    g(x) = 2
q(x) = x² – x + 7;     r(x) = 0

(ii) deg q(x) = deg r(x)
∴ this is possible when
deg of both q(x) and r(x) should be less than p(x) and g(x).
p(x) = x³+ x² + x + 1;    g(x) = x² – 1
q(x) = x + 1,    r(x) = 2x + 2

(iii) deg r(x) is 0.
This is possible when product of q(x) and g(c) form a polynomial whose degree is equal to degree of p(x) and constant term.