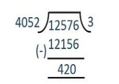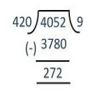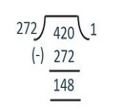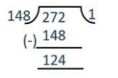1.1 Euclid’s Division Lemma:
Theorem 1. Given positive integers a and b, there exists unique integers q and r satisfying a = b q + r, where o ≤ r < b. Euclid’s division algorithm is based on this lemma.
What is an Algorithm?
An algorithm is a series of well-defined steps which gives a procedure for solving a type of problem.
What is a Lemma?
A lemma is a proven statement used for proving another statement.
Example 1: Use Euclid’s algorithm to find the HCF of 4052 and 12576.
Sol: Since 12576 > 4052, we divide 12576 by 4052
12576 = 4052 × 3 + 420
Since the remainder in not 0, we divide 4052 by 420,
4052 = 420 × 9 + 272
Since the remainder in not 0, we divide 420 by 272,
420 = 272 × 1 + 148
Since the remainder is not 0, we divide 272 by 148,
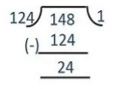
272 = 148 × 1 + 124
Since the remainder is not 0, we divide 148 by 124,
148 = 124 × 1 + 24
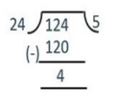
Since the remainder is not 0, we divide 124 by 24,
124 = 24 × 5 + 4
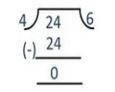
Since the remainder is not 0, we divide 24 by 4,
24 = 4 × 6 + 0
The remainder has now become zero, so our procedure stops. Since the divisor at this stage is 4, the HCF of 12576 and 4052 is 4.
Note: Euclid’s division lemma and algorithm are so closely interlinked that people often call former as the division algorithm also.
Applications of Euclid’s Division:-
Example 1: Show that every positive even integer is of the form 2q, and that every positive odd integer is of the form 2q +1,where q is some integer
Sol: Let a = positive integer and b = 2
By Euclid’s algorithm, a = 2q + r, for some integer q ≥ 0, so a = 2q or 2q + 1
If a is of the form 2q, then a is an even integer.
Also, a positive integer can be either even or odd.
Therefore, any positive odd integer is of the form 2q + 1.
Example 2:– Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is some integer.
Sol: Let us start with taking a, where a is a positive odd integer.
We apply the division algorithm with a and b = 4
Since o ≤ r < 4, the possible remainders are 0, 1, 2 and 3.
a can be 4q or 4q + 1 or 4q + 3
Example 3: A sweet seller has 420 kaju barfis and 130 badam barfis. She wants to stack them in such a way that each stack has the same number, and they take up the least area of the tray. What is the number of that can be placed in each stack for this purpose?
Sol: Ignoring the trial and error method, we can do it accurately by finding HCF (420, 130). Now, let us use Euclid’s algorithm to find their HCF. We have:
420 = 130 × 3 + 30 (420÷130)
130 = 30 × 4 + 10 (130÷30)
30 = 10 × 3 + 0 (30÷3)
So, the HCF of 420 and 130 is 10.
Therefore, the sweet seller can make stacks of 10 for both kinds of barfi.
EXERCISE 1.1
Q1. Use Euclid’s division algorithm to find the HCF of:
(i) 135 and 225 (ii) 196 and 38220 (iii) 867 and 255
Sol:
(i) Since 225 is greater, 225 ÷135
Using Euclid division algorithm we get 225=135 × 1+9 135÷90
135 = 90 × 1+ 45
90 = 45 × 2 + 0 Now r = 0
45 is HCF of (225, 135)
(ii) Since 38220 is greater, 38220 ÷ 196
Using Euclid division algorithm
38220 = 196 × 195 + 0 Now r = 0,
196 is HCF of (196, 38220)
(iii) Since 867 is greater,
867 ÷ 255 (Using Euclid division algorithm)
867 = 255 × 3+102
255 ÷ 102
255 = 102 × 2+51
102 ÷ 51
102 = 51 × 2 + 0
Now r = 0, 51 is HCF (102, 51)
Q2. Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Sol: By Euclid’s Division Lemma
For a and b any two positive integer, we can always find unique integer q and r such that a = bq+ r, where 0 ≤ r < b
Let us take a as any positive integers and b = 6, Then using Euclid’s algorithm we get,
a = 6q + r as 0 ≤ r < 6, the possible remainders are r = 0, 1, 2, 3, 4, 5
So total possible forms will 6q+0, 6q+1, 6q+2, 6q+3, 6q+4, 6q+5
a = 6q + r, where 0 ≤ r < 6
a = 6q + 0 × a = 6q, (even number)
a = 6q + 1 × a = 6q + 1, (odd number)
a = 6q + 2× a = 6q + 2, (even number as 6 and 2 are divisible by 2)
a = 6q + 3 × a = 6q + 3, (it is not divisible by 2)
a = 6q + 4 × a = 6q + 4, (t is divisible by 2)
a = 6q + 5 × a = 6q + 5 , (it is not divisible by 2)
So 6q, 6q + 2, 6q + 4 (are even number)
6q + 1 ,6q + 3, 6q + 5 (are odd numbers)
Q3. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Sol: According to the question, we need to find the maximum number of columns
Maximum number of columns is the HCF of number 32 and 616
Since 616 is greater,
616 ÷ 32
By using Euclid division algorithm.
616 = 32 × 19 + 8
Again 32 ÷ 8
By using Euclid division formula
32 = 8 × 4 + 0
As r = 0, 8 is the HCF of 616 and 32.
The maximum number of columns in which they can march = 8.
4. Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Hint: [Let x be any positive integer then it is of the form 3q, 3q + 1 or 3q + 2.
Squaring: 3q2 = 3m , 3q2+1 =3m + 1, 3q2+2 = 3m+ 2 ]
Sol: Let a be any positive integer, and b = 3.
By using Euclid’s Division Algorithm, a = 3q + r, as 0 ≤ r < 3,
The possible remainders are r = 0, 1, 2
So total possible forms will 3q + 0, 3q + 1, 3q + 2
a = 3q, a2 = 9q2 = 3m where m = 3q2
a = 3q + 1,
a2 = 9q2 + 6q + 1 = 3 (3q2 + 2q) +1 = 3m + 1 where m = (3q2 + 2q)
a2 = 9q2 + 12q + 4 = 3 (3q2 + 4q + 1) + 1 = 3m + 1 where m = 3q2 + 4q + 1
5. Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8
Sol: Euclid’s Division Lemma
For a and b any two positive integer, we can always find unique integer q and r such that a = bq + r, where 0 ≤ r < b
Let us take a as any positive integers and b = 3,
Then using Euclid’s algorithm we get, a = 3q + r where 0 ≤ r < 3,
The possible remainders are r = 0, 1, 2
So total possible forms will 3q + 0, 3q + 1, 3q + 2
a = 3q, a3 = 27q3 = 9m where m = 3q3 and a = 3q + 1,
Cubing both sides we get
a3 = 27q3 + 27q2 + 9q + 1
= 9 ( 3q3 + 3q + q) + 1 = 9m + 1
where m = 3q3 + 3q + q
a = 3q + 2, Cubing both sides we get
a3 = 27q3 + 54q2 + 36q + 8
= 9 (3q3 + 6q + 4q) + 8
where m = 3q3 + 6q + 4q
Additional Practice Questions:
Q1.Use Euclid’s division algorithm to find the HCF of:
(i) 320 and 132 (ii) 130 and 91 (iii) 648 and 1400
Q2. Show that any positive odd integer is of the form 8q + 1, or 8q + 3, or 8q + 5, where q is some integer.
Q3. Sunil has 160 blue marbles and 80 white ones. If he wants to place them in identical groups without any marbles left over, what is the greatest number of groups Sunil can make?
Q4. Use Euclid’s division lemma to show that the square of any positive integer is either of the form 5m or 5m + 1 for some integer m.