1.4 Revisiting Rational Numbers:
Theorem 1.5:
Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form \frac { p }{ q } , where p and q are co prime, and the prime factorisation of q is of the form 2n 5n, where n, m are non-negative integers.
Theorem 1.6:
Let x = \frac { p }{ q } be a rational number, such that the prime factorisation of q is of the form 2n 5n, where n, m are non-negative integers. Then x has a decimal expansion which terminates.
Theorem 1.7
Let x = \frac { p }{ q } be a rational number, such that the prime factorisation of q is of the form 2n 5n, where n, m are non-negative integers. Then x has a decimal expansion which is non-terminating repeating (recurring).
EXERCISE 1.4
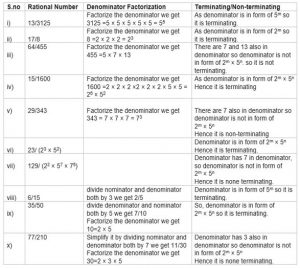
1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or non-terminating repeating decimal expansion
Sol: We know that for terminating decimal expansion of a rational number of form p/q , q must be of the. form 2m × 5n
2.Write down the decimal expansions of those rational numbers in Above which have terminating decimal expansions.
Sol:
(i) (13/3125) = (13/55 ) = 13 × (25/(25 x 55 )) = (416/105) = 0.00416
(ii) (17/8) = (17/23 ) = 17 × (53/(23 x 53 ) = 17 × (53/103 ) = (2125/103 ) = 2.125
(iv) (15/1600) = (15/24 ) × 102 = 15 × (54 / (24 x 54)) × 102 = (9375 / 106 ) = 0.009375
(vi) 23/(23 52 ) = 23 × 53 × (22 /(23 x 52 ) × 53 × 23 = (11500/ 103 ) = 0.115
(viii) 6/15 = 2/5 = 2 × 2/5 ×2 = 4/10 = 0.4
(ix) 35/50 = 7/10 = 0.7
3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form p, q you say about the prime factors of q.
(i) 43.123456789
(ii) 0.120120012000120000…
(iii) 43.123456789
Sol: (i) Since this number has a terminating decimal expansion, it is a rational number of the form \frac { p }{ q } p, and q is of the form 2m × 5 n.
(ii) The decimal expansion is neither terminating nor recurring. Therefore, the given number is an irrational number.
(iii) Since the decimal expansion is non-terminating recurring, the given number is a rational number of the form \frac { p }{ q } , and q is not of the form 2m × 5n