ADDITIONAL QUESTIONS AND ANSWERS:
1. What is the HCF of the smallest composite number and the smallest prime number?
Ans: Smallest composite number = 4
Smallest prime number = 2
So, HCF (4, 2) = 2
2. If HCF of a and b is 12 and product of these numbers is 1800.
Then what is LCM of these numbers?
Ans: Product of two numbers = Product of their LCM and HCF
⇒ 1800 = 12 × LCM
⇒ LCM = 1800/12 = 150.
3. What is the HCF of 33 × 5 and 32 × 52?
Ans: HCF of 33 × 5 and 32 × 52
= 32 × 5 = 45
4. A number N when divided by 14 gives the remainder 5. What is the remainder when the same number is divided by 7?
Ans: It will be 5, because 14 is multiple of 7.
Therefore, remainder in both cases will be the same.
5. Examine whether 17/30 is a terminating decimal or not.
Ans:
![]()
Since the denominator has 3 as its factor.
∴ 17/30 is a non terminating decimal.
6. A rational number in its decimal expansion is 1.7351. What can you say about the prime factors of q when this number is expressed in the form p/q ? Give reason.
Ans: As 1.7351 is a terminating decimal number, so q must be of the form 2m 5n,
where in, n are natural numbers.
7. Without actually performing the long division, find 987/10500 will have terminating or non
terminating repeating decimal expansion. Give reason for your answer.
Ans: 987/10500 = 47/500
and 500 = 22 × 53,
so it has terminating decimal expansion.
8. Can the number 4n, n be a natural number, end with the digit 0? Give reason.
Ans: If 4n ends with 0, then it must have 5 as a factor.
But, (4)n = (22)n = 22n i.e., the only prime factor of 4n is 2.
Also, we know from the fundamental theorem of arithmetic that the prime factorization of each number is unique.
∴ 4n can never end with 0.
9. Write a rational number between √3 and √5.
Ans: A rational number between √3 and √5 is √3.24
√3.24 = 1.8 = 18/10 = 9/5
10. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Ans: For the maximum number of columns, we have to find the HCF of 616 and 32.
Now, since 616 > 32, we apply division lemma to 616 and 32.
We have, 616 = 32 × 19 + 8
Here, remainder 8 ≠ O.
So, we again apply division lemma to 32 and 8.
We have, 32 = 8 × 4 + O
Here, remainder is zero. So, HCF (616, 32) = 8
Hence, maximum number of columns is 8.
11. Find the LCM and HCF of 12, 15 and 21 by applying the prime factorisation method.
Ans: The prime factors of 12, 15 and 21 are
12 = 22 × 3, 15 = 3 × 5 and 21 = 3 × 7
Therefore, the HCF of these integers is 3.
22, 31, 51 and 71 and are the greatest powers involved in the prime factors of 12, 15 and 21.
So, LCM (12, 15, 21) = 22 × 31 × 51 × 71 = 420.
12. There is a circular path around a sports field. Sita takes 18 minutes to drive one round of the field, while Ronil takes 12 minutes for the same. Suppose they both start from the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Ans: To find the time after which they meet again at the starting point,
we have to find LCM of 18 and 12 minutes. We have
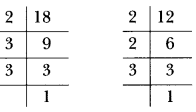
Therefore, LCM of 18 and 12 = 22 × 32 = 36
So, they will meet again at the starting point after 36 minutes.
13. Express the number 0.\overline{3178} in the form of rational number a/b
Ans: Let x = 0. \overline{3178}
then x = 0.3178178178 … … (1)
10x = 3.178178178 … …(ii) ( Multiply by 10)
10000x = 3178.178178… …(iii) ( Multiply by 10000)
On subtracting (ii) from (iii), we get
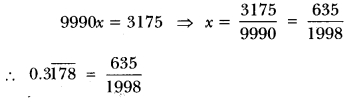
14. The LCM of two numbers is 14 times their HCF.
The sum of LCM and HCF is 600.
If one number is 280, then find the other number.
Ans: Let HCF of the numbers be x then
according to question LCM of the number will be 14x
And sum of HCF and LCM = x + 14x = 600
⇒ 15x = 600 ⇒ x = 40
Then HCF = 40 and LCM = 14 × 40 = 560
∵ LCM × HCF = Product of the numbers
560 × 40 = 280 × Second number
Second number = (560 × 40)/280 = 80
Then other number is 80
15. Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Ans: Let a be the positive integer.
Then by Euclid’s division algorithm, corresponding to the positive integers a and 3 there exists non-negative integers q and r such that
a = 3q + r where 0 ≤ r < 3
a2 = 9q2 + 6qr + r2 …. (i) 0 ≤ r < 3
Case – I: When r = 0 [putting in (i)]
a2 = 9q2 = 3(3q2) = 3m where m = 3q2
Case – II: r = 1
a2 = 9q2+6q + 1 = 3 (3q2 + 2q)+ 1
= 3m + 1 where m = 3q2 + 2q
Case – III: r = 2
a2 = 9q2 + 12 + 4 = 3 (3q2 + 4q + 1) + 1
= 3m + 1 where m = (3q2 + 4q + 1)
Hence, square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
16. The product of two consecutive integers is divisible by 2.
Is this statement true or false? Give reason.
Ans: True, because n (n + 1) will always be even,
as one out of the n or n+ 1 must be even.
17. Explain why 3 × 5 × 7 + 7 is a composite number.
Ans: 3 × 5 × 7 + 7 = 7 (3 × 5 + 1) = 7 × 16, which has more than two factors.
Since it has more than two factors it is composite
18. What is the least number that is divisible by all the numbers from 1 to 10?
Ans: Required number = The LCM of 1, 2, 3, … 10 = 2520
19. Show that any positive odd integer is of the form 6q + 1 or 6q + S or 6q + 5 where q is some integer.
Ans: Let a he any positive odd integer and h = 6. Then, by Euclid’s algorithm,
a = 6q + r, for some integer q ≥ 0 and 0 ≤ r < 6.
i.e., the possible remainders are 0, 1, 2, 3, 4, 5.
Thus, a can be of the form 6q, or 6q + I, or 6q + 2, or 6q + 3, or 6q + 4,
or 6q + 5, where q is some integer.
Since a. is odd integer, so a cannot be of the form , or 6q+ 2, or 6q + 4, (since they are even).
Thus, a is of the form 6q + 1, 6q + 3, or 6q + 5, where q is some integer.
Hence, any odd positive integer is of the form 6q + 1 or 6q + 3 or 6q + 5, where q is some integer.
20. Use Euclid’s division algorithm to find the HCF of 960 and 432
Ans: Since 960 > 432, we apply the division lemma to 960 and 432.
We have, 960 = 432 × 2 + 96
Since the remainder 96 ≠ 0, so we apply the division lemma to 432 and 96.
We have, 432 = 96 × 4 + 48
Again remainder 48 ≠ 0 so we again apply division lemma to 96 and 48.
We have, 96 = 48 × 2 + O
The remainder has now become zero. So our procedure stops.
Since the divisor at this stage is 48.
Hence, HCF of 960 and 432 is 48.
i.e., HCF (960, 432) = 48
