MULTIPLE CHOICE QUESTIONS. (MCQ’s)

1. In which of the following triangles are all sides equal.

(a) Scalene 
(b) Equilateral
(c) Isosceles
(d) Right angled

2. Area of any equilateral triangle with side as ‘a’ is  ____

(a) \frac { 3 }{ \sqrt { 2 } } a
(b) \frac { 3 }{ \sqrt { 2 } } { a }^{ 2 }
(c) \frac { \sqrt { 3 } }{ 4 } { a }^{ 2 }
(d) \frac { \sqrt { 3 } }{ 2 } { a }^{ 2 }

3. The diagonals of a rhombus are 8 cm and 6 cm so the side of the rhombus will be___ 

(a) 5 cm
(b) 5\sqrt { 2 } cm
(c)\sqrt { 7 }
(d) 3 cm

4. The corresponding sides of two similar triangles are in the ratio 3:4 the area of the smaller triangle is 54 cm^{2 .} So the area of bigger triangle   will be____

(a) 40 cm² 
(b) 96 cm² 
(c) 60 cm² 
(d) 85 cm² 

5. The perimeter of a scalene triangle is 42 cms. if two of its
sides are 17 cm and 18 cm find the third side

(a) 11 cm
(b) 19 cm
(c) 7 cm
(d) 12 cm

6. Triangles are special types of______

(a) Polygons
(b) Quadrilaterals
(c) Circles
(d) None of the above

7. If a line divides any two sides of a triangles in the same ratio then
the line must be ____to the third line.

(a) Adjacent
(b) Corresponding
(c) Equal
(d) Parallel

8. If one angle of triangle is equal to one angle of the other triangle and the sides including these angles are ____ then the two triangles are similar

(a) Proportional
(b) Equal
(c) In the same ratio
(d) None of the these

9. The  sides of two similar triangles are in the ratio 4:9 so the
areas of these triangles will be in the ratio_____

(a) 8:18
(b) 16:81
(c) 24:48
(d) 32:64

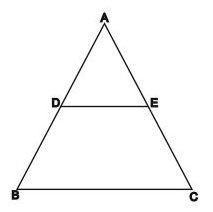
10. In the given fig.

DE\parallel BC and \frac { ae }{ ac } =\frac { 3 }{ 8 } if ab = 2.4cm find ad.

(a) 9/10
(b) 6/7
(c) 7/10
(d) 11/12

11. In a right angled triangle the ____ of the hypotenuse is equal to the
sum of the ____ of the other two sides

(a) Square, cubes
(b) Square , square
(c) Sides, sides
(d) Angle, angles

12. The Pythagoras theorem rule can be used for _____ triangles 

(a) Isosceles
(b) Equilateral
(c) Right angled
(d) Scalene

13. The ratio of the areas of two similar triangle is equal to the ____ of the ratio of corresponding sides 

(a) Cube
(b) Total
(c) Sum
(d) Square

14. Two figures are said to be ____ if they have the same shape and size

(a)  Similar
(b) Equal
(c) Congruent
(d) None of the above

15. Basic proportionality theorem is also called ______ Theorem

(a) Euclid’s
(b) Rananujan
(c) Theolus
(d) Thales  

16. The line segment joining the mid-points of the adjacent sides of a quadrilateral form a _____

(a) Hexagon     
(b) Rhombus      
(c) Parallelogram      
(d) Trapezium

17. In the figure.  OA = 3x−19 , OC=x −3
OB = x −4 and OD = 4. The value of x is__

(a) 8 or 11    
(b) 10 or 11    
(c) 5 or 6    
(d) 17 or 18

18. If the corresponding sides of two triangles are proportional then they are similar. This is also called____ similarity criterion.

(a) A A S   
(b) S S S   
(c)  S A S  
(d)  A S A

19. In this figure lines AB and CD intersect at point O and  ∠AOC = 50°

∴ ∠AOC= ___

(a) 110°  
(b) 80°   
(c) 60°   
(d) 130°

20. In the figure the vertical opposite angles are___

(a) ∠AOY , ∠AOX     
(b) ∠XOY , ∠BOY   
(c) ∠BOX , ∠XOY   
(d) ∠AOY , ∠BOX

21. The areas of two similar triangles are in the ratio of the squares of the corresponding___

(a) Medians  
(b) Altitudes  
(c) Angles  
(d) None of these

22. If ∠ABC ~ ∠DEF such that AB = 12 cm and DE = 1.4 cm. Then the ratio
of the areas of ΔABC and ΔDEF is ___

(a) 16 : 25  
(b) 9 : 25 
(c) 25 : 36   
(d) 36 : 49

23. If ΔABC ~ΔDEF and area of ΔABC is 9cm² and area of ΔDEF is 16cm²
BC = 21cm. then length EF =___

(a) 2.8 cm   
(b) 3.5 cm  
(c) 1.8 cm   
(d) 2.6 cm

24. A right angled triangle has hypotenuse x cm and side is y cm. If x −y =1.
Then the length of third side is___

(a)√ 2x + y       
(b)√ 2y +1   
(c)√   x + y
(d) √ 2x −1 

25. A ladder 25m reaches the window of a house 20m about the ground. The
distance of the foot of the ladder from the house is____

(a) 22 m   
(b) 25 m   
(c) 10 m  
(d) 15 m

26. Area of an equilateral triangle is ____

(a) √3/4a²   
(b) √ 2 /4a²      
(c) √ 2 /8a²    
(d) √ 5 /3a²

27. If ΔABC and ΔDEF are similar triangles such that
∠A = 40° and ∠E = 80°  Then ∠C =___

(a) 50°   
(b) 60°    
(c) 70°   
(d) 40°

28. The length of the hypotenuse of an isosceles right triangle whose
one side is 4√2cm will be ____

(a) 6 cm   
(b) 8 cm   
(c) 10 cm    
(d) 5 cm

29. ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm,
then the perimeter of ΔDEF is ______
(a) 10 cm
(b) 14 cm
(c) 30 cm
(d) 25 cm

30. In the given figure ΔABC ~ ΔPQR. The value of x is_____

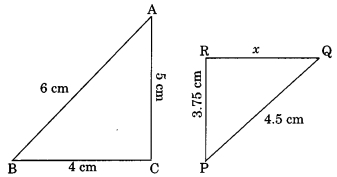
(a) 2.5 cm
(b) 3.5 cm
(c) 2.75 cm
(d) 3 cm

31. The perimeter of a isosceles triangle is 45 cms. If one of the
equal side is 16 cm. Find the third side
(a) 12.5 cm
(b) 13 cm
(c) 15 cm
(d) 31 cm

32. In a triangle the straight line drawn from the vertex to the midpoint of the opposite side is called as _____
(a) Median   
(b) Altitude  
(c) Angle   
(d) None of these

33. In a triangle the straight line drawn from the vertex perpendicular to the opposite side is called as _____
(a) Median   
(b) Altitude  
(c) Angle   
(d) None of these

34. In a right angled triangle ABC right angled at B, what will be the value of ∠C  +  ∠A
(a) 50°   
(b) 60°    
(c) 70°   
(d) 90°

35. The exterior angle of a triangle is equal to the sum of the interior ______ angles
(a)  Similar
(b) Equal
(c) Congruent
(d) Opposite

Answers. + Clues.

1 (b) ⇒ Refer definition

2 (c) ⇒ Formula of area of equilateral triangle

3 (a) ⇒ Diagonals bisect each other. So the rhombus will be form four right angled triangles then by Pythagoras theorem, find any one side of any one triangle

4 (b) ⇒ Area of 1st triangle/area of 2nd triangle = \frac { { side }^{ 2 } }{ { side }^{ 2 } }   (use formula from (text book)

5 (c) ⇒ Perimeter = sum of all sides

6 (a) ⇒ (Text book)

7 (d) ⇒ Converse of B.P.T

8 (a) ⇒ Definition of S.A.S congruency

9 (b) ⇒ Area of triangle (I)/area of triangle = (first ratio / second ratio )²

10 (a) ⇒ Use B.P.T rule

11 (b) ⇒ Pythagoras theorem

12 (c) ⇒ Pythagoras theorem

13 (d) ⇒ Summary text book

14 (c) ⇒ Congruent figures definition

15 (d) ⇒ (Text book)

16 (c) ⇒ Definition.

17 (a) ⇒ Since the diagonals of a trapezium divide each other in proportion we get AO/OC = OB/OD.

18 (b) ⇒ S.S.S definition

19 (d)  ⇒ ∠AOD + ∠AOC = 180° (linear pair)

20 (d) ⇒ Definition of vertically opposite angles

21 (a) ⇒   Theorem

22 (d) ⇒ Area of ΔABC/Area of ΔDEF  =  (AB)²/(DE)²

23 (a) ⇒ Area of ΔABC/Area of ΔDEF  =  (AB)²/(DE)²

24 (b) ⇒ (Hypotenuse)² =(side)²+ (side)²

25 (d) ⇒ Use Pythagoras theorem after drawing a rough figure.

26 (a) ⇒ Formula of area of equilateral triangle.

27 (b) ⇒ Since the triangles are similar ∠A = ∠D, ∠B =∠E and ∠C =∠F

28 (b) ⇒ Use Pythagoras theorem and in an isosceles triangle two sides are equal.

29 (a) ⇒ Perimeter of ΔABC / Perimeter of  ΔDEF (x)   = AC/DF . 

30 (d) ⇒  AB/PQ = BC/QR. Put the values and find x

31. (b) ⇒  In an isosceles triangle two sides are equal. 

32. (a) ⇒ Definition of Median

33. (b) ⇒ Definition of Altitude

34.(d) ⇒  Value of a right angle is 90°

35.(d) ⇒  Exterior angle Axiom