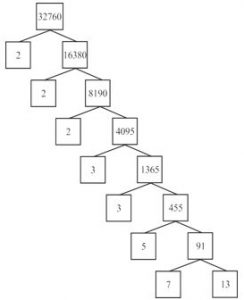
1.2 The Fundamental Theorem of Arithmetic:
Hence we factorise 32760 as 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13.
32760 = 23 × 32 × 5 × 7 × 13 as a product of primes.
Thus we can conclude that every composite number can be written as the product of powers of primes. Hence we can say that, this is true, and is called the Fundamental Theorem of Arithmetic because of its basic crucial importance in the study of integers.
Theorem 1.2 (Fundamental Theorem of Arithmetic):
Every composite number can be expressed (factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur.
Note: Carl Friedrich Gauss is often referred to as the ‘Prince of Mathematicians’
The Fundamental Theorem of Arithmetic says that every composite number can be factorised as a product of primes.
The prime factorisation of a natural number is unique, except for the order of its factors.
EXAMPLES:
Q1: Consider the numbers 4n, where n is a natural number. Check whether there is any value of n for which 4n ends with the digit zero.
Sol: If the number 4n, for any n, were to end with the digit zero, then it would be divisible by 5. That is, the prime factorisation of 4n would contain the prime number 5.
This is not possible because 4n = (2) 2n; so the only prime in the factorisation of 4n is 2.
So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorisation of 4n.
So, there is no natural number n for which 4n ends with the digit zero.
Q2. Find the LCM and HCF of 6 and 20 by the prime factorisation method.
Sol: We have 6 = 2¹ × 3¹ and 20 = 2 × 2 × 5 = 2² × 5¹.
HCF (6, 20) = 2 and LCM (6, 20) = 2 × 2 × 3 × 5 = 60.
LCM (6, 20) = 2² × 3¹ × 5¹
Thus HCF (6, 20) × LCM (6, 20) = 6 × 20.
In fact, we can verify that for any two positive integers a and b,
HCF (a, b) × LCM (a, b) = a × b.
| Note: We can use this result to find the LCM of two positive integers, if we have already found the HCF of the two positive integers. |
Q3: Find the HCF of 96 and 404 by the prime factorisation method.Then find their LCM.
Sol: The prime factorisation of 96 and 404 gives:
96 = 2 x 2 x 2 x 2 x 2 x 3, 404 = 2 x 2 x 101
Therefore, the HCF of these two integers is 2×2 = 4.
Also, LCM 96,104 = \frac { 96\times 102 }{ hcf(96104) } =\frac { 96\times 104 }{ 4 } =9696
Q4: Find the HCF and LCM of 6, 72 and 120, using the prime factorisation method.
Sol: We have: 6 = 2 x 3, 72 = 2 x 2 x 2 x 3 x 3,
and 120 = 2 x 2 x 2 x 3 x 5
Here, 2 and 3 are the smallest common factors found in all the three numbers
So, HCF of (6, 72, 120) = 2 × 3 = 6
23, 32 and 51 are the greatest powers of the prime factors 2, 3 and 5 respectively involved in the three numbers.
Therefore LCM (6, 72, 10) = 23 × 32 × 51
= 2 x 2 x 2 x 3 x 3 x 5 = 360.
EXERCISE 1.2
1. Express each number as product of its prime factors:
Sol:
(i) 140 = 2 × 2 × 5 × 7 = 22 × 5 × 7
(ii) 156 = 2 × 2 × 3 × 13 = 22 × 3 × 13
(iii) 3825 = 3 × 3 × 5 × 5 × 17 = 32 × 52 × 17
(iv) 5005 = 5 × 7 × 11 × 13
(v) 7429 = 17 × 19 × 23
2.Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(i) 26 and 91 (ii) 510 and 92 (iii) 336 and 54
Sol: (i) Prime Factorization of the Numbers
26 = 2 × 13
91 = 7 × 13
HCF = 13 and LCM = 2 × 7 × 13 = 182
Product of two numbers 26 × 91 = 2366
Product of HCF and LCM 13 × 182 = 2366
Hence, product of two numbers = product of HCF × LCM
(ii) Prime Factorization of the Numbers
510 = 2 × 3 × 5 × 17
92 = 2 × 2 × 23
HCF = 2 and LCM = 2 × 2 × 3 × 5 × 17 × 23 = 23460
Product of two numbers 510 × 92 = 46920
Product of HCF and LCM 2 × 23460 = 46920
Hence, product of two numbers = product of HCF × LCM
(iii) Prime Factorization of the Numbers
336 = 2 × 2 × 2 × 2 × 3 × 7
54 = 2 × 3 × 3 × 3
HCF = 2 × 3 = 6 and LCM = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7 = 3024
Product of two numbers 336 × 54 = 18144
Product of HCF and LCM 6 × 3024 = 18144
Hence, product of two numbers = product of HCF × LCM.
3.Find the LCM and HCF of the following integers by applying the prime factorization method.
(i) 12, 15 and 21 (ii) 17, 23 and 29 (iii) 8, 9 and 25
Sol:
(i) Prime Factorization of the Numbers
12 = 2 x 2 x 3 = 22 x 3
15 = 3 x 5 , 21 = 3 x 7
H.C.F = 3 and L.C.M = 22 x 3 x 5 x 7 = 420
(ii) Prime Factorization of the Numbers
17 = 1 × 17, 23 = 1 × 23 , 29 = 1 × 29
HCF = 1
LCM = 1 × 17 × 19 × 23 = 11339
(iii) Prime Factorization of the Numbers
8 = 2 × 2 × 2 ×1 , 9 = 3 × 3 ×1, 25 = 5 × 5 × 1
HCF =1
LCM = 1 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 1800
4. Given that HCF (306, 657) = 9, find LCM (306, 657).
Sol: We know the formula that
Product of LCM and HCF = product of the numbers
LCM × 9 = 306 × 657
Dividing both sides by 9 we get
LCM = (306 × 657) 9 = 22338
5. Check whether 6n can end with the digit 0 for any natural number n.
Sol: If any digit has last digit 10 that means it is divisible by 10 and the factors of 10 = 2 × 5
So value 6n should be divisible by 2 and 5
Now (2 × 3) n is divisible by 2 and 3, but not divisible by 5, so it can not end with 0.
6. Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers
Sol: Since, 7 × 11 × 13 +1 3
=13 (7 × 11 + 1)
= 13 × (77 + 1)
=13 × 78
= 13 × 13 × 6
=13 × 13 × 3 × 2
Since, it has more than two factors (13 x 78) and (1, 2, 3, 13)
It is a composite number.
7 × 6 × 5 × 4 × 3 × 2 ×1 +5
= 5 (7 × 6 × 4 × 3 × 2 × 1)
= 5 (1008 + 1) = 5 (1009)
Since it has more than two factors (5 × 1009) and (1, 5, 1009)
It is a composite number.
7.There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Sol: The time of their meeting is the LCM of 18 and 12 in minutes.
Prime factorisation of 18 =2 × 3 × 3
Prime factorisation of 12 = 2 × 2 × 3
Hence, LCM of 18, 12 = 2 × 3 × 3 × 2 = 36
Sonia and Ravi meet after 36 minutes.
Additional Practice Questions:
(Q1).Using Euclid’s Division Algorithm, find the HCF of 6496 and 376
(Q2) In a school annual day function parade, a group of 1309 students need to march behind the band of 408 members. The two groups have to march in the same number of columns. What is the maximum number of columns in which they can march?
(Q3) Show all the prime factors of 1778700
(Q4) Two tankers contain 1482 litres and 779 litres of petrol respectively. Find the maximum capacity of the container which can measure the petrol of either tanker in exact number of litres.
(Q5) Find the largest positive integer that will divide 1638 and 1082 leaving remainders 26 and 16 respectively.