Tangents to a Circle:
All the tangents of a circle are perpendicular to the radius through the point of contact of that tangent.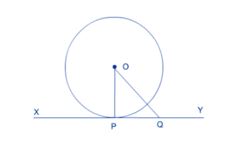
OP is the radius of the circle and Q is any point on the line XY which is the tangent to the circle. As OP is the shortest line of all the distances of the point O to the points on XY. So OP is perpendicular to XY. Hence, OP⊥ XY
Example 1 : Find the radius of the circle in the given figure, if the length of the tangent from point A which is 5 cm away from center is 4 cm.
Solution : As we know that the radius is perpendicular to the radius, so the ∆ABO is a right angle triangle.
Given, AO = 5 cm and AB = 4 cm
We can use Pythagoras theorem here
OA 2= OB 2 + AB 2
OB 2= OA 2 − AB 2
OB 2= 5 2 − 4 2
= 25 – 16
OB 2 = 9 ⇒ OB = 3
So the radius of the given circle is 3 cm.
Exercise: 10.1
1.How many tangents can a circle have.
Solution: There can be infinite tangents to a circle. A circle is made up of infinite points which are at an equal distance from a point. Since there are infinite points on the circumference of a circle, infinite tangents can be drawn from them.
2.Fill in the blanks:
(i) A tangent to a circle intersects it in …………… point(s).
(ii) A line intersecting a circle in two points is called a ………….
(iii) A circle can have …………… parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called …………
Solution: (i) A tangent to a circle intersects it in one point(s).
(ii) A line intersecting a circle in two points is called a secant.
(iii) A circle can have two parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called the point of contact.
3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm.
Length PQ is : (A) 12 cm (B) 13 cm (C) 8.5 cm (D) √119cm
Solution:
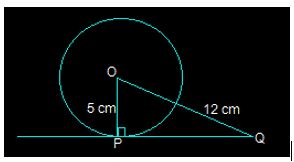
In the above figure, the line that is drawn from the centre of the given circle to the tangent PQ is perpendicular to PQ.
And so, OP ⊥ PQ
Using Pythagoras theorem in triangle ΔOPQ we get,
OQ2 = OP2 + PQ2
(12)2 = 52+ PQ2
PQ2= 144 − 25
PQ2 = 119 ⇒ PQ = √119 cm
So, option D.
4. Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:
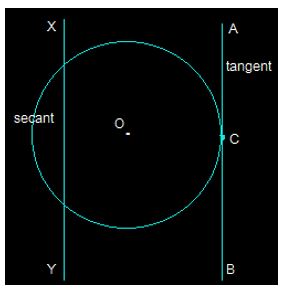
In the above figure, XY and AB are two the parallel lines. The line segment AB is the tangent at point C while the line segment XY is the secant.
