SELF TEST:
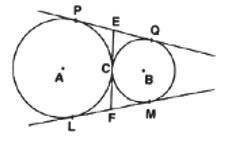
1. In the following figure, two circle touch each other externally at C. Prove that the common tangent at C bisects the other two common tangents. ( 2 mk )
2. In the figure, if Ab = AC, prove that BE = CE. ( 2 mk )
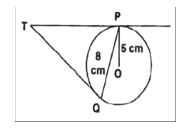
3. A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12 cm. Find the radius of the circle. ( 2 mk )
4. A circle is touching the side BC of ∆ ABC at P and touching AB and AC produced at Q and R respectively. Prove that : AQ = 1/2 ( Perimeter of ∆ ABC ) ( 2 mk )
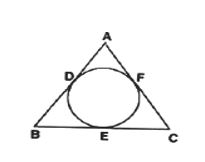
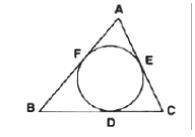
5. The incircle of ∆ ABC touches the sides BC, CA and AB at D, E and F respectively.
Show that: AF+ BD + CD = AE + BF + CE
= 1/2 ( Perimeter of ∆ ABC ) ( 2 mk )
6. Show that the tangents drawn at the end points of a diameter of a circle are parallel. ( 2 mk )
7. In the figure PQ is a chord of a circle and PT is the tangent at P such that
∠QPT = 60°, Find ∠PRQ. ( 2 mk )
8. PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length of TP. ( 2 mk )
.
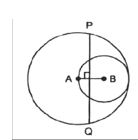
9. In the figure, two circles with centres A and B and radii 5 cm and 3 cm touching each other internally. If the perpendicular bisector of segment AB, meets the bigger circle at P and Q, find the length of PQ. ( 2 mk )
10. Two tangents making an angle of 120° with each other, are drawn to a circle of radius 6 cm. Show that the length of each tangent is 2√3 cm. ( 2 mk )