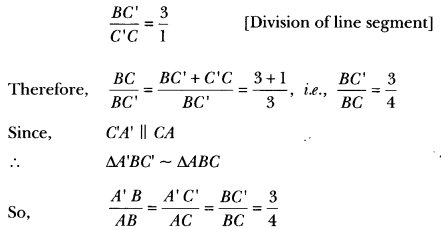ADDITIONAL QUESTIONS AND ANSWERS:
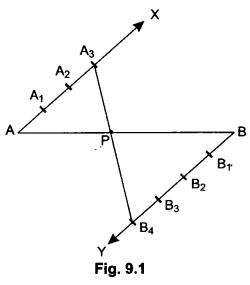
1) In Fig. 9.1 by what ratio does P divide AB internally.
Sol:
From Fig. 9.1, it is clear that there are 3 points at equal distances on AX and 4 points at equal distances on BY. Here P divides AB on joining A3 B4. So P divides internally by 3 : 4.
2) Given a triangle with side AB = 8 cm. To get a line segment AB’ = 2 of AB, in what ratio will line segment AB be divided?
Sol:
Given AB = 8 cm
AB’ = 3/4 of AB
= 3/4 × 8 = 6 cm
BB’ = AB – AB’ = 8 – 6 = 2 cm.
⇒ AB’: BB’ = 6 : 2 = 3 : 1
Hence the required ratio is 3 : 1.
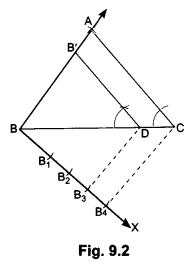
3) Draw a triangle with sides 4 cm, 5 cm and 6 cm. Then construct another triangle whose sides are 2/3 of the corresponding sides of first triangle.
Sol:
Steps of Construction:
Step I: Draw a line segment BC = 6 cm
Step II: Draw an arc with B as centre and radius equal to 5 cm.
Step III: Draw an arc, with C as centre and radius equal to 4 cm intersecting the previous drawn arc at A.
Step IV: Join AB and AC, then ∆ABC is the required triangle.
Step V: Below BC make an acute angle CBX
Step VI: Along BX mark off three points at equal distance: B1, B2, B3, such that BB1 = B1B2, = B2B3.
Step VII: Join BC3.
Step VIII: From B2, draw B2, D || B3,C, meeting BC at D.
Step IX: From D draw ED || AC meeting BA at E. Then we have ∆EDB which is the required triangle.
Justification:
Since DE || CA
![]()
Hence, we have the new ΔEBD similar to the given ∆ABC, whose sides are equal to 2/3 of the corresponding sides of ∆ABC.
4) Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Sol:
Steps of Construction:
Step I: Draw a line segment AB = 7.6 cm
Step II: Draw any ray AX making an acute angle ∠BAX with AB.
Step III: On ray AX starting from A, mark 5 + 8 = 13 equal arcs. AA1, A1A2, A2A3, A3A4, … A11A12, and A12A13.
Step IV: Join A13B.
Step V: From A5, draw A5P || A13B, meeting AB at P. Thus, P divides AB in the ratio 5 : 8. On measuring the two parts. We find AP = 2.9 cm and PB = 4.7 cm (approx).
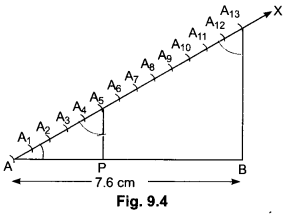
Justification:
In ∆ABA13, PA5 || BA13 .
∴ By Basic Proportionality Theorem
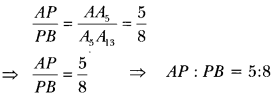
5) Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then draw another triangle whose sides are 1½ times the corresponding sides of the isosceles triangle.
Sol:
Steps of Construction:
Step 1: Draw BC = 8 cm.
Step II: Construct XY, the perpendicular bisector of line segment BC, meeting BC at M.
Step III: Along MP, cut-off MA = 4 cm.
Step IV: Join BA and CA. Then ∆ABC so obtained is the required ∆ABC.
Step V: Extend BC to D, such that BD = 12 cm
Step VI: Draw DE || CA meeting BA produced at E. Then ΔEBD is the required triangle.
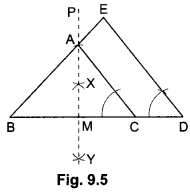
Justification:
Since, DE || CA .
![]()
Hence, we have the new triangle similar to the given triangle whose sides are 1½ ( 3/2 ) times the corresponding sides of the isosceles ΔABC.
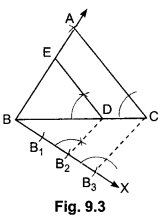
6) Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides of the corresponding sides of ΔABC.
Sol:
Steps of Construction:
Step 1: Construct a ∆ABC in which BC = 6 cm and, AB = 5 cm and ∠ABC = 60°.
Step II: Below BC make an acute ∠CBX.
Step III: Along BX mark off four arcs: B1, B2, B3 such that BB1 = B1B2 = B2B3 = B3B4.
Step IV: Join B4C.
Step V: From B3, draw B3D || B4C, meeting BC at D.
Step VI: From D, draw ED || AC, meeting BA at E.
Now, we have ΔEBD which is the required triangle whose sides are 34th of the corresponding sides of ∆ABC.
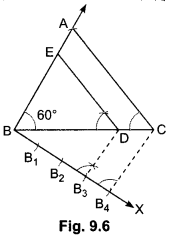
Justification:
Here, DE || CA
∴ ∆ABC ~ ∆EBD.
![]()
Hence, we get the new triangle similar to the given triangle whose sides are equal to 34th of the corresponding sides of ∆ABC.
7) Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Sol:
Steps of Construction:
Step 1: Take a point O and draw a circle of radius 6 cm.
Step II: Take a point P at a distance of 10 cm from the centre 0.
Step III: Join OP and bisect it. Let M be the mid-point.
Step IV: With M as centre and MP as radius, draw a circle to intersect the circle at Q and R.
Step V: Join PQ and PR. Then, PQ and PR are the required tangents.
On measuring, we find, PQ = PR = 8 cm.
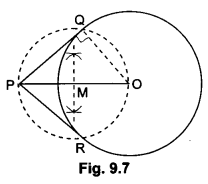
Justification:
On joining OQ, we find that ∠PQO = 90°, as ∠PQO is the angle in the semicircle.
∴ PQ ⊥ OQ
Since OQ is the radius of the given circle, PQ has to be a tangent to the circle.
Similarly, PR is also a tangent to the circle.
8) Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Sol:
Steps of Construction:
Step 1: Take a point O and draw a circle of radius OA = 4 cm. Also, draw a concentric circle of radius OB = 6 cm
Step II: Find the mid-point C of OB and draw a circle of radius OC = BC. Suppose this circle intersects the circle of radius 4 cm at P and Q.
Step III: Join BP and BQ to get the desired tangents from a point B on the circle of radius 6 cm.
By actual measurement, we find BP = BQ = 4.5 cm.
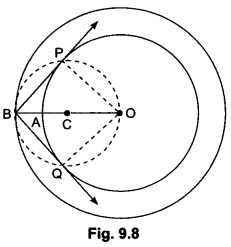
Justification:
In ∆BPO, we have
∠BPO = 90°, OB = 6 cm and OP = 4 cm
∴ OB2 = BP2 + OP2 [Using Pythagoras theorem]
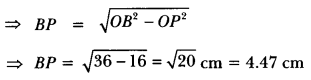
Similarly, BQ = 4.47 cm
9) Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Sol:
Steps of Construction:
Step I: Draw a line segment AB = 8 cm.
Step II: With A as centre, draw a circle of radius 4 cm and let it intersect the line segment AB in M.
Step III: With B as centre, draw a circle of radius 3 cm.
Step IV: With M as centre, draw a circle of radius AM and let it intersect the given two circles in P, Q and R, S.
Step V: Join AP, AQ, BR and BS.
These are the required tangents.
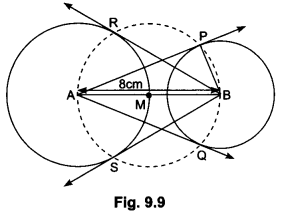
Justification:
On joining BP, we have ∠BPA = 90°, as ∠BPA is the angle in the semicircle.
∴ AP ⊥ PB
Since BP is the radius of given circle, so AP has to be a tangent to the circle.
Similarly, AQ, BR and BS are the tangents.
10) Construct a triangle similar to a given triangle ABC with its sides equal to 5/3 of the corresponding sides of the triangle ABC .
Sol:
Steps of Construction:
Step I: Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
Step II: From B cut off 5 arcs
B1, B2, B3, B4 and B5 on BX so that
BB1 = B1B2 = B2B3 = B3B4 = B4B5.
Step III: Join B3 to C and draw a line through B5, parallel to B3C intersecting the extended line segment BC at C’.
Step IV: Draw a line through C’ parallel to CA intersecting the extended line segment BA at A’ (see figure).
Then, A’ BC’ is the required triangle.
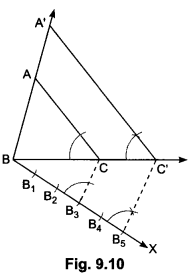
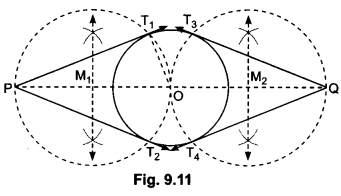
Justification:
Note that ∆ABC ~ ∆A’BC” (Since AC || A’C’)
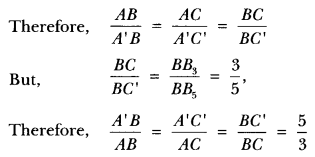
11) Draw a circle of radius of 3 cm. Take two points P and Q on one of its diameters extended on both sides, each at a distance of 7 cm on opposite sides of its centre. Draw tangents to the circle from these two points P and Q.
Sol:
Steps of Construction:
Step 1: Taking a point ( as centre, draw a circle of radius 3 cm.
Step II: Take two points P and Q on one of its extended diameter such that OP = OQ = 7 cm.
Step III: Bisect OP and OQ and let M1 and M2 be the mid-points of OP and OQ respectively.
Step IV: Draw a circle with M1 as centre and M1 P as radius to intersect the circle at T1, and T2.
Step V: Join PT1 and PT2.
Then, PT1 and PT2 are the required tangents. Similarly, the tangents QT3 and QT4 can be obtained
Justification:
On joining OT1, we find ∠PT1O = 90°, as it is an angle in the semicircle.
PT1 ⊥ OT1
Since OT1 is a radius of the given circle, so PT1 has to be a tangent to the circle.
Similarly, PT2, QT3 and QT4 are also tangents to the circle
12) Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Sol:
Steps of Construction:
Step I: Construct a SABC in which BC = 4 cm, ∠B = 90° and BA = 3 cm.
Step II: Below BC, make an acute ∠CBX.
Step III: Along BX mark off five arcs: B1, B2, B3, B4 and B5 such that
BB1 = B1B2 = B2B3 = B3B4 = B4B5.
Step IV: Join B3C.
Step V: From B5, draw B5D || B3C, meeting BC produced at D.
Step VI: From D, draw ED || AC, meeting BA produced at E. Then ΔEBD is the required triangle whose sides are 5/3 times the corresponding sides of ∆ABC.
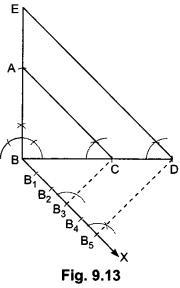
Justification:
Since, DE || CA
![]()
Hence, we have the new triangle similar to the given triangle whose sides are equal to 5/3 times the corresponding sides of ∆ABC.
13) Construct a triangle similar to a given triangle ABC with its sides equal to 3/4 of the corresponding sides of the triangle ABC .
Sol:
Steps of Construction:
Step I: Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
Step II: Locate 4 arcs B1, B2, B3, and B4 on BX so that
BB1 = B1B2 = B2B3 = B3B4.
Step III: Join B4C and draw a line through B3 parallel to B4C to intersect BC at C’.
Step IV: Draw a line through C’ parallel to the line CA to intersect BA at A’ (Fig. 9.14).
Then, ∆A’ BC’ is the required triangle.
Let us now see how this construction gives the required triangle.
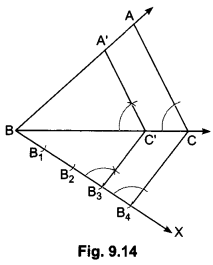
Justification: