MULTIPLE CHOICE QUESTIONS: (MCQ’s)
1. The shape of an ice−cream cone is a combination of____
(a) Sphere + cylinder
(b) Sphere + cone
(c) Hemisphere + cylinder
(d) Hemisphere + cone
2. If a cone is cut parallel to the base of it by a plane in two parts, then the shape of the top of the cone will be a____
(a) Sphere
(b) Cube
(c) Frustum of Cone
(d) Cylinder
3. If we cut a cone in two parts by a plane parallel to the base, then the bottom part left over is the____
(a) Cone
(b) Frustum of cone
(c) Sphere
(d) Cylinder
4. If r is the radius of the sphere, then the surface area of the sphere is given by____
(a) 4 π r2
(b) 2 π r2
(c) π r2
(d) 4/3 π r2
5. If we change the shape of an object from a sphere to a cylinder, then the volume of cylinder will ____
(a) Increase
(b) Decrease
(c) Remains unchanged
(d) Doubles
6. Fifteen solid spheres are made by melting a solid metallic cone of
base diameter 2 cm and height 15 cm. The radius of each sphere is____
(a) 1/2
(b) 1/4
(c) 1/√2
(d) 1/√4
7. The radius of the top and bottom of a bucket of slant height 35 cm
are 25 cm and 8cm. The curved surface of the bucket is____
(a) 4000 sq.cm
(b) 3500 sq.cm
(c) 3630 sq..cm
(d) 3750 sq.cm
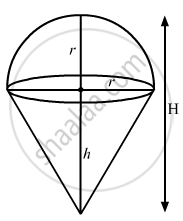
8. This figure is made up of two figures they are ____ and ____
(a) cone + cylinder
(b) cone + circle
(c) cylinder + circle
(d) hemisphere + cone
9. A cone of height 21 cm and radius of base is 6 cm therefore the volume will be ____
(a) 800 cm
(b) 792 cm
(c) 872 cm
(d) 972 cm
10. The radii of the ends of a frustum of a cone 14cm high are 2cm and 7cm
therefore the volume will be_____ cm3
(a) 3485/3
(b) 2948/3
(c) 3048/3
(d) 2900/3
10. The formula for CSA of frustum of cone is ____
(a) \Pi l({ r }_{ 1 }+{ r }_{ 2 })
(b) \Pi ({ r }_{ 1 }+{ r }_{ 2 })
(c) \frac { \Pi }{ 2 } ({ r }_{ 1 }+{ r }_{ 2 })
(d) none of the above
11. The lateral surface area of a cuboid = ____
(a) 2(l − b ) x h
(b) 2 (l + b) h
(c) 3 ( l + b ) x h
(d) 1/2 (l + b ) x h
12. CSA of a hollow cylinder is ____
(a) 2\Pi h({ R }^{ 2 }+r)
(b) 2\Pi h({ r }^{ 2 }+R)
(c) 2\Pi h({ R }^{ 2 }−r)
(d) 2\Pi ({ R }^{ 2 }+r)
13. TSA of hemisphere is ____
(a) 4\Pi r^{ 2 }
(b) 4\Pi r^{ 3 }
(c) 3\Pi r^{ 2 }
(d) 4\Pi r^{ 4 }
14. The volumes of two spheres are in the ratio 27 : 8. The ratio of their curved surface is____
(a) 9 : 4
(b) 4 : 9
(c) 3 : 2
(d) 2 : 3
15. The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is_____
(a) 27 : 20
(b) 20 : 27
(c) 9 : 4
(d) 4 : 9
16. If the radius of base of a right circular cylinder is halved, keeping the height same, the ratio of the volume of the reduced cylinder to that of the original cylinder is____
(a) 2 : 3
(b) 3 : 4
(c) 1 : 4
(d) 4 : 1
17. If the volumes of a cube is 1728 cm³, the length of its edge is equal to____
(a) 7 cm
(b) 12 cm
(c) 18 cm
(d) 19 cm
18. The circumference of the edge of hemispherical bowl is 132 cm. When π is
taken as 227, the capacity of bowl in cm³ is______
(a) 2772
(b) 924
(c) 19404
(d) 9702
19. The surface areas of two spheres are in the ratio 1 : 2.
The ratio of their volume is____
(a) √2 : 1
(b) 1 : 2√2
(c) 1 : 8
(d) 1 : 4
20. Two cubes each of volume 8 cm³ are joined end to end, then
the surface area of the resulting cuboid is_____
(a) 80 cm²
(b) 64 cm²
(c) 40 cm²
(d) 8 cm²
21. A cylindrical pencil sharpened at one edge is combination of____
(a) a cone and a cylinder
(b) frustum of a cone and cylinder
(c) a hemisphere and a cylinder
(d) four cylinders
22. Taking π = 22/7, if surface area of a sphere is 616 cm²,
then its diameter is ____
(a) 7 cm
(b) 14 cm
(c) 56 cm
(d) 28 cm
23. The curved surface area of a right circular cone of height 15 cm
base diameter 16 cm² is___
(a) 60π cm²
(b) 68π cm²
(c) 1200π cm²
(d) 136π cm²
24. A shuttle cock used for playing badminton has the shape of a combination of____
(а) a cylinder and a sphere
(b) a cylinder and a hemisphere
(c) a cone and a sphere
(d) a frustum of a cone and a hemisphere
25. The total surface area of a solid hemisphere of radius r is_____
(a) 47πr²
(b) 2πr²
(c) 43πr³
(d) 3πr²
26. Any object having a definite shape and size is called a ______
(a) Cylinder
(b) Solid
(c) Cuboid
(d) Fluid
27. Solids like pipes,pencils,road rollers,circular pillars are examples of ______
(a) Cylinders
(b) Cones
(c) Cuboids
(d) Spheres
28. A cylinder and a cone are of the same base radius and same height.The ratio of the cylinder and the cone will be ____
(a) 3:4
(b) 3:1
(c) 1:3
(d) 2:5
29. Curved surface area for a hollow cylinder is ____
(a) 3πh(R + r)
(b) 2πh(R + r²)
(c) 2πh(R + r)
(d) 2π²h(R + r)
30. Books, match box, almirah are all examples of ______
(a) Cylinders
(b) Cones
(c) Cuboids
(d) Spheres
31. Solids like cricket balls,oranges,rubber ball,etc are all examples of _____
(a) Cylinders
(b) Cones
(c) Cuboids
(d) Spheres
32. Total surface area of a frustrum of a cone is ___
(a) π(R²+r²+l)(R+r)
(b) π(R²+r²+l)(R+r)
(c) π(R²+r²+l)(R+r)
(d) π(R²+r²+l)(R+r)
33. A medicinal capsule is in the shape of a cylinder. We can split this up into_____
(a) Sphere + cylinder
(b) Sphere + cone
(c) Hemisphere + cylinder
(d) 2Hemispheres + cylinder
34. Slant height of a cone is _____
(a) l² = r² + h²
(b) l² = 2r² + h²
(c) l² = r² + 2h²
(d) 2l² = r² + h²
35. A cone and a hemisphere have the same values for r and h. Then the ratio of their volumes is ____
(a) 3 : 2
(b) 1 : 2
(c) 2 : 3
(d) 1 : 4
Answers + Clues:
1 : (d) ⇒ Observe an ice cream cone
2 : (c) ⇒ Make a paper cone and see
3: (b) ⇒ Textbook (Activity 1)
4 : (a) ⇒ Use formula
5 : (c) ⇒ Height of cylinder = twice radius of sphere
6 : (d) ⇒ Use volume of cone and volume of sphere
7 : (c) ⇒ C S A of frustum of cone
8 : (b) ⇒ Use volume of cone formula
9 : (b) ⇒ Use volume of frustum of cone formula
10 : (a) ⇒ C S A of frustum of cone formula
11 : (b) ⇒ L S A of cuboid formula
12 : (d) ⇒ Formula of C S A of hollow cylinder
13 : (a) ⇒ Formula of S A of sphere
14 : (c) ⇒ Formula of T S A of hemisphere.
15 : (b) ⇒ Compare the two volume of cylinder formulas
16 : (c) ⇒ First radius =r and second radius = r/2 and h = h. Then compare volumes
17 : (b) ⇒ Use volume of cube formula and find cube root of the given volume
18 : (c) ⇒ Circumference = 2πr .Find r .Then find volume of hemisphere
19 : (b) ⇒ Ratio of S.A gives r1 = 1 and r2 = √2 Then compare volumes
20 : (c) ⇒ Side of cube =2cm..Then find using surface area of cuboid
21 : (a) ⇒ Put an imaginary line on the upper part of pencil
22 : (b) ⇒ Use surface area formula find r . then double it
23 : (d) ⇒ First find slnt height. Then use CSA formula
24 : (d) ⇒ Observe a shuttlecock
25 : (d) ⇒ Formula of TSA of hemisphere
26: (b) ⇒ Definition of solid
27: (a) ⇒ Examples of a cylinder
28: (b) ⇒ Compare the volumes of both
29: (c) ⇒ Formula of CSA of hollow cylinder
30: (c) ⇒ Examples of a cuboids
31: (d) ⇒ Examples of a spheres
32: (a) ⇒ Formula of TSA of frustrum of cone
33: (d) ⇒ Roughly split the figure into 3 parts
34: (a) ⇒ Formula of slant height of cone
35: (b) ⇒ Compare the volumes of both