ADDITIONAL QUESTIONS AND ANSWERS:
1). Find the number of zeroes.
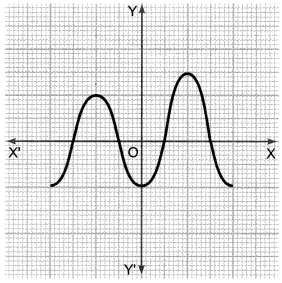
Ans: The number of zeros is four as the graph intersects the X− axis at four points
2. Find the number of zeroes.
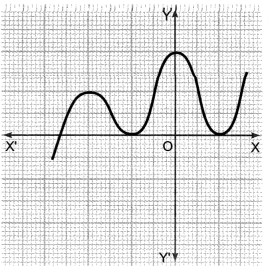
Ans: The number of zeros is three as the graph intersects the X−axis at three points
3. If on division of a polynomial p(x) by a polynomial g(x), the quotient is zero, what is the relation between the degrees of p(x) and g(x).
Ans: Since the quotient is zero, therefore
deg p(x) < deg g(x)
4. If one zero of the quadratic polynomial x2 – 5x – 6 is 6 then find the other zero.
Ans: Let x² −5x − 6 = (x−6) (x−1)
∴ x = 6, −1
So, the other zero is −1.
5. If both the zeros of the quadratic polynomial ax2 + bx + c are equal and opposite in sign, then find the value of b.
Ans: Let α and −α be the roots of given polynomial.
Then α + (−α) = 0 ⇒ −b/a =0 ⇒ b = 0. (sum of roots =−b/a)
6. What number should be added to the polynomial x2 – 5x + 4, so that 3 is the zero of the polynomial?
Ans: Let f(x) = x2 – 5x + 4
Then f (3) = 32 – 5 x 3 + 4 = −2
For f (3) = 0,
2 must be added to f(x).
7. Can a quadratic polynomial x2 + kx + k have equal zeros for some odd integer k > 1?
Ans: No, for equal zeros, k = 0, 4
⇒ k should be even.
8. If the zeros of a quadratic polynomial ax2 + bx + c are both negative, then can we say a, b and c all have the same sign? Justify your answer.
Ans: Yes, because −b/a = sum of zeros < 0, so that (−b/a) = 0 > 0.
Also the product of the zeros = (c/a) = 0 > 0.
9. If the graph of a polynomial intersects the x-axis at only one point, can it be a quadratic polynomial?
Ans: Yes, because every quadratic polynomial has at the most two zeros.
10. If one of the zeros of the quadratic polynomial f(x) = 4x2 – 8kx – 9 is equal in magnitude but opposite in sign of the other, find the value of k.
Ans: Let one root of the given polynomial be α.
Then the other root = −α
Sum of the roots = (−α) + α = 0
⇒ −b/a = 0 or −(−8k/4 )= 0 or k = 0
11. If one of the zeros of the quadratic polynomial (k – 1)x2 + kx + 1 is −3 then find the value of k.:
Ans: Since – 3 is a zero of the given polynomial
∴ (k – 1)(−3)2 + k(−3) + 1 = 0 :
⇒ 9k – 9 – 3k + 1 = 0
⇒ k = 4/3.
12. If 1 is a zero of the polynomial p(x) = ax2 – 3(a – 1)x −1,
then find the value of a.
Ans: Put x = 1 in p(x)
∴ p(1) = a(1)2 – 3(a – 1) x 1 – 1 = 0
⇒ a – 3a + 3 – 1 = 0
⇒ 2a = −2 ⇒ a = 1
13. If α and β are zeros of polynomial p(x) = x2 – 5x + 6, then find the value of α + B – 3αß.
Ans: Here, α + β = 5, and αβ = 6
= α + β – 3αβ = 5 – (3 x 6 )=5 −18 = −13
14.Find the zeros of the polynomial p(x) = 4x2 – 12x + 9.
Ans: p(x) = 4x2 – 12x + 9 = (2x – 3)2
For zeros, p(x) = 0
⇒ (2x – 3)(2x – 3) = 0
⇒ x = 3/2 and 3/2
15. If one root of the polynomial p(y) = 5y2 + 13y + m is reciprocal of other, then find the value of m.
Ans:
![]()
16. If α and β are zeros of p(x) = x2 + x – 1, then find 1α+1β
Ans: Here, α + β = −b/a = −1/1 = −1
So 1α + 1β = −1.
17. Find a quadratic polynomial with the given numbers −1/4, 1/4 as the sum and product of its zeros respectively.
Ans: Let α, β be the zeros of polynomial.
(i) We have, α + β = −1/4 and αβ = 1/4
Thus, polynomial is
p(x) = x² – ( α + β ) x + αβ
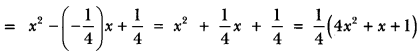
Quadratic polynomial 4x2 + x + 1
18. Find the zeros of the following quadratic polynomials and verify the relationship between the zeros and the coefficients Q(1 – 2).
(i) 6x2 – 3 – 7x
Ans: We have, p(x) = 6x2 – 3 – 7x
p(x) = 6x2 – 7x – 3
(In general form)
= 6x2 – 9x + 2x – 3 = 3x (2x – 3) + 1 (2x – 3)
= (2x – 3) (3x + 1)
The zeros of polynomial p(x) is given by
p(x) = 0) = (2x – 3) (3x + 1) = 0
⇒ x = 32, −13
Thus, the zeros of 6x2 – 7x – 3 are α = −3/2 and β = −1/3
Now, sum of the zeros = α + β
= 3/2−1/3 = (9−2)/6 = 7/6

(ii) 4u2 + 8u
Ans: We have, p(u) = 4u2 + 8u = p(u) = 4u (u + 2)
The zeros of polynomial p(u) is given by
p(u) = 0 ⇒ 4u (u + 2) = 0 .
∴ u = 0, −2
Thus, the zeros of 4u2 + 8u are α = 0 and β = −2
Now, sum of the zeros = α + β = 0 – 2 = −2

19. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(ii) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
Ans: (i) We have,
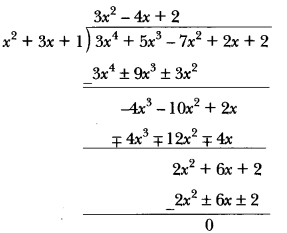
Remainder is zero, so x²+ 3x + 1 is a factor of polynomial
3x4 + 5x3 – 7x2 + 2x + 2
(ii) We have,
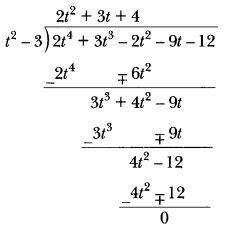
Remainder is zero, so t² – 3 is a factor of polynomial
2t4 + 3t3 – 2t2 – 9t – 12.
20. Find a quadratic polynomial each with the given numbers as the sum and product of its zeros respectively.
(i) −/4, 1/4 (ii) √2 ,1/3
Ans: Let α, β be the zeros of polynomial.
(i) We have, α + β = −1/4 and αβ = 1/4
Thus, polynomial is
p(x) = x² – (α +β ) x + αβ

Quadratic polynomial 4x2 + x + 1
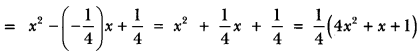
(ii) We have, α + β = √2 and αβ = 1/3
Thus, polynomial is p(x) = x2 – (α + β) x + αβ
= x2 – √2x + 1/3 = 1/3 (3x2 – 3√2x + 1)
Quadratic polynomial = 3x2 – 3√2x + 1
21. What must be subtracted from p(x) = 8x4 + 14x3 – 2x2 + 7x – 8 so that the resulting polynomial is exactly divisible by g(x) = 4x2 + 3x – 2?
Ans: Let y be subtracted from polynomial p(x)
: 8x4 + 14x3 – 2x2 + 7x – 8 – y is exactly divisible by g(x)
Now,
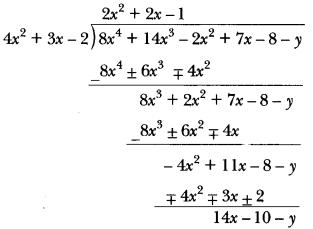
∵ Remainder should be 0.
∴ 14x – 10 – y = 0 or 14x – 10 = y or y = 14x – 10
∴ (14x – 10) should be subtracted from p(x) so that
it will be exactly divisible by g(x)
