Ex 2.4
1) Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 – 5x + 2; 14, 1, −2
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Solution:
(i) Comparing the given polynomial with ax3 + bx2 + cx + d, we get:
a = 2, b – 1, c = −5 and d = 2.
∴ p(x) = 2x3 + x2 – 5x + 2

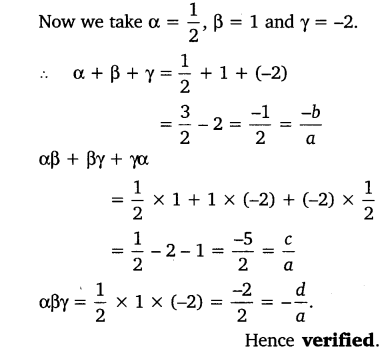
(ii) Comparing the given polynomial with ax3 + bx2 + cx + d, we get:
a = 1, b = −4, c = 5 and d = – 2.
∴ p (x) = x3 – 4x2 + 5x – 2
⇒ p(2) = (2)3 – 4(2)2 + 5 x 2 – 2
= 8 – 16+ 10 – 2 = 0
p(1) = (1)3 – 4(1)2 + 5 x 1−2
= 1 – 4 + 1 – 2
= 6−6 = 0
Hence, 2, 1 and 1 are the zeroes of x3 – 4x2 + 5x – 2.
Hence verified.
Now we take α = 2, β = 1 and γ = 1.
α + β + γ = 2 + 1 + 1 = 41 = −ba
αβ + βγ + γα = 2 + 1 + 2 = 51 = ca
αβγ = 2 x 1 x 1 = 21 = −da.
Hence verified.
2) Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, −7, −14 respectively.
Solution:
Let α , β and γ be the zeroes of the required polynomial.
Then α + β + γ = 2, αβ + βγ + γα = −7 and αβγ = −14.
∴ Cubic polynomial
= x3 – (α + β + γ)x2 + (αβ + βγ + γα)x – αβγ
= x3 – 2x2 – 1x + 14
Hence, the required cubic polynomial is x3 – 2x2 – 7x + 14.
3) If the zeroes of the polynomial x3 – 3x2 + x + 1 are a-b, a, a + b, find a and b.
Solution:
Let α , β and γ be the zeroes of polynomial x3 – 3x2 + x + 1.
Then α = a−b, β = a and γ = a + b.
∴ Sum of zeroes = α + β + γ
⇒ 3 = (a – b) + a + (a + b)
⇒ (a – b) + a + (a + b) = 3
⇒ a−b + a + a + b = 3
⇒ 3a = 3
⇒ a = 33 = 1 …(i)
Product of zeroes = αβγ
⇒ −1 = (a – b) a (a + b)
⇒ (a – b) a (a + b) = −1
⇒ (a2 – b2) a = −1
⇒ a3 – ab2 = −1 … (ii)
Putting the value of a from equation (i) in equation (ii), we get:
(1)3 −(1)b2 = −1
⇒ 1 – b2 = −1
⇒ – b2 = −1 – 1
⇒ b2 = 2
⇒ b = ±√2
Hence, a = 1 and b = ±√2.
4) If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± √3, find other zeroes.
Solution:
Since two zeroes are 2 + √3 and 2 – √3,
∴ [x−(2 + √3)] [x− (2 – √3)]
= (x−2− √3)(x−2 + √3)
= (x−2)2– (√3)2
x2 – 4x + 1 is a factor of the given polynomial.
Now, we divide the given polynomial by x2 – 4x + 1.
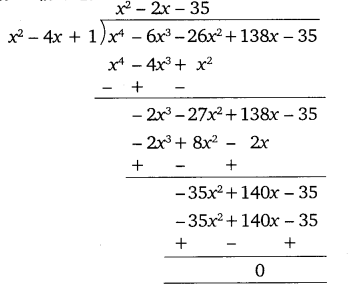
So, x4 – 6x3 – 26x2 + 138x – 35
= (x2 – 4x + 1) (x2 – 2x – 35)
= (x2 – 4x + 1) (x2 – 7x + 5x – 35)
= (x2 −4x + 1) [x(x− 7) + 5 (x−7)]
= (x2 – 4x + 1) (x – 7) (x + 5)
Hence, the other zeroes of the given polynomial are 7 and −5.
5) If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:
We have
p(x) = x4 – 6x3 + 16x2 – 25x + 10
Remainder = x + a … (i)
Now, we divide the given polynomial 6x3 + 16x2 – 25x + 10 by x2 – 2x + k.
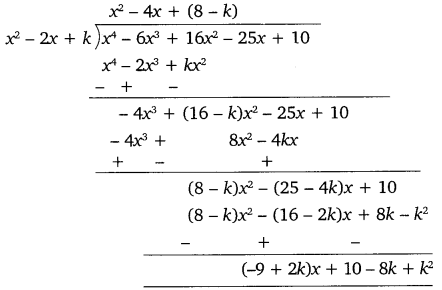
Using equation (i), we get:
(−9 + 2k)x + 10−8 k + k2 = x + a
On comparing the like coefficients, we have:
−9 + 2k = 1
⇒ 2k = 10
⇒ k = 102 = 5 ….(ii)
and 10 −8k + k2– a ….(iii)
Substituting the value of k = 5, we get:
10 – 8(5) + (5)2 = a
⇒ 10 – 40 + 25 = a
⇒ 35 – 40 = a
⇒ a = −5
Hence, k = 5 and a = −5.
