MULTIPLE CHOICE QUESTIONS: (MCQ’s)
1.The zeroes of the quadratic polynomial x² + 99x + 127 are _____ .
(a) Both positive
(b) Both negative
(c) One positive ,one negative
(d) Both are same
2.If the zeroes of the quadratic polynomial x² +bx+c, c≠0 are equal then ___
(a) c and a have opposite signs
(b) c and b have opposite signs
(c) c and a have same signs
(d) c and b have same signs
3.The number of polynomials having zeroes as −2 and 5 is ___.
(a) 1
(b) 2
(c) 3
(d) more than 3
4.The degree of the polynomial (x+1) (x²−x−x³ +1 is ____.
(a) 2
(b) 3
(c) 4
(d) 5
5. If the zeroes of the quadratic polynomial x² + (a + 1) x + b are 2 and −3 then ____.
(a) a= −7 , b= −1
(b) a = 5 , b = −1
(c) a = 2 , b = −6
(d) a = 0 , b = −6
6. If one of the zeroes of a quadratic polynomial ax² + bx + c is 0,
then the other zero is ____
(a) −b/a
(b) 0
(c) b/a
(d) −c/a
7. If one of the zeros of the quadratic polynomial (k−1) x² + k + 1 is −3 then k = ___.
(a) 4/3
(b) −4/3
(c) 2/3
(d) −2/3
8.If α and β are the zeros of x² −4x + 1 then 1/α + 1/β − αβ is ________.
(a) 3
(b) 5
(c) −5
(d) −3
9.If (x + 1) is a factor of x² −3ax + 3a−7 then value of a is ___ .
(a) 1
(b) −1
(c) 0
d)−2
10. What is the value of x2 −2x − 4 at (x = −1)
(a) +1
(b) −1
(c) +2
(d) − 2
11. Curves that are either open upwards or open downwards depending
on whether a>0 or a<0 are called____
(a) Co ordinates
(b) Equations
(c) Graph
(d) Parabolas
12. A polynomials p(x) of degree ‘n’ has ___ number of zeros
(a) x
(b) n
(c) y
(d) a
13. The zero of a linear polynomials ax + b is _____
(a) −b/a
(b) +b/a
(c) −b2/a
(d) +b2/a
14. The zeros of x2 + 7x + 10 are _____
(a) (x + 2) (x + 5)
(b) (x + 2) (x − 5)
(c) (x − 2) (x − 5)
(d) (x − 2) (x + 5)
15. We know that dividend = divisor x quotient + _____
(a) Last term
(b) Zero
(c) First term
(d) Remainder
16. If p(x) and g(x) are any two polynomials with g(x) ≠ 0 then we can
find polynomials q(x) and r(x) such that p(x) is ____
(a) g (x) x q(x) + r(x)
(b) g (x) x q(x) − r(x)
(c) g (x) + q(x) x r(x)
(d) g (x) − r (x) x q(x)
17. The zeros of 3x + 4 is ___
(a) −3/4
(b) +4/3
(c) −4/3
(d) +3/4
18. The product of the zeros of the quadratic polynomials 6x2 + 5x − 2 is ____.
(a) −1/2
(b) +1/3
(c) −1/3
(d) +1/2
19. If the product of zeros of the polynomials ax2 − 6x − 6 is 4 then value of ‘a’ is ____.
(a) −3/2
(b) + 1/3
(c) −1/3
(d) + 1/2
20. If ∝ and β are the zeros of the polynomial x + 6x + 5 then the value of ( ∝ + β )² is ____
(a) 36
(b) 16
(c) −36
(d) 25
21. The zeroes of the quadratic polynomial x² −5 is ____
(a) ± √5
(b) √5
(c) −√5
(d) √3
22. p(x) = 3x + 2 is a polynomial .The variable here is ___
(a) 3
(b) 2
(c) x
(d) y
23. A polynomial of degree 0 is called a _____polynomial.
(a) Linear
(b) Quadratic
(c) Constant
(d) None of these
24. The curve that represents the graph of the polynomial
f(x) = x² − 2x − 8 is called a _____
(a) Line of symmetry
(b) Co ordinate
(c) Axis
(d) Parabola
25. The polynomial f(x) = x²−6x + 9 has two equal roots .They are ____
(a) √5 ,√5
(b) 3, 3
(c) √3 ,√3
(d) 3,−3
26. The maximum number of zeros that a polynomial of degree 4 can have is ___
(a) One
(b) Two
(c) Three
(d) Four
27. The graph of the polynomial p(x) = 3x – 2 is a straight line which intersects the x-axis at exactly one point namely _____
(a) (− \frac{2}{3} , 0)
(b) (0 , − \frac{2}{3} )
(c) ( \frac{2}{3} , 0)
(d) ( \frac{2}{3}, − \frac{2}{3} )
28. In fig. given below, the number of zeros of the polynomial f(x) is ____
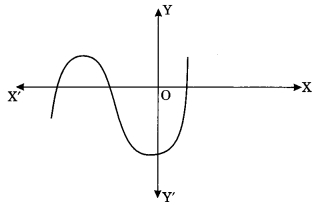
(a) 1
(b) 2
(c) 3
(d) None
29. The graph of the polynomial ax² + bx + c is an upward parabola if ____
(a) a > 0
(b) a < 0
(b) a = 0
(d) None
30. The graph of the polynomial ax² + bx + c is a downward parabola if ____
(a) a > 0
(b) a < 0
(c) a = 0
(d) a = 1
31. A polynomial of degree 3 is called a ____
(a) Linear polynomial
(b) Quadratic polynomial
(c) Cubic polynomial
(d) Biquadratic polynomial
32. If α, β are the zeros of the polynomial x² – 16, then αβ(α + β) is _____
(a) 0
(b) 4
(c) −4
(d) 16
33. If Α and Β are the zeros of the polynomial ax² + bx + c, then value of ΑΒ is ____
(a) 0
(b) −c/a
(c) −a/c
(d) 1
34. Zeros of the polynomial x² – 11 are _____
(a) ± √11
(b) ± √3
(c) 0
(d) None
35. If the sum of the zeros of the polynomial f(x) = 2x³ – 3kx² + 4x – 5 is 6, then the value of k is _____
(a) 2
(b) 4
(c) −2
(d) −4
Answers + Clues :
1: (b) ⇒ Use the formula x =\frac { -b\pm \sqrt { { b }^{ 2 } } −4ac }{ 2a }
2: (c) ⇒ If co-efficient of { x }^{ 2 } and constant terms have same sign then zeroes are equal
3: (d) ⇒ Required number of polynomials are infinite
4: (d) ⇒ Variables with highest power is the degree (multiply and then write the degree)
5: (d) ⇒ Solve the given equation and find the two roots .First root =2 and second root = −3
6: (a) ⇒ a + 0 = −b/a a = −b/a
7: (a) ⇒ Put (x = −3) in the equation = 6k −8 = 0
8: (a) ⇒ Find the two zeros from the given equation and put these values
9: (a) ⇒ If (x + 1) is a factor then x = −1
10 : (b) ⇒ Put (−1) in place of x in the given equation and solve it
11 : (d) ⇒ Definition of parabola
12 : (b) ⇒ (Textbook)
13 : (a) ⇒ (Textbook 2.3)
14 : (a) ⇒ Split the middle term & solve
15 : (d) ⇒ (textbook 2.4)
16: (a) ⇒ (Textbook)
17 : (c) ⇒ Simplify it
18 : (c) ⇒ Use product of zeros formula
19 : (a) ⇒ Use product of zeros formula
20 : (a) ⇒ Use the sum formula ( ∝ + β ) =−b/a
21 : (a)⇒ Solve the equation x² −5 = 0 and find value of x
22 : (c) ⇒ The unknown number.
23 : (c) ⇒ Definition of constant polynomial.
24 : (d) ⇒ Definition of Parabola
25 : (b) ⇒ Solve f(x) = x²−6x +9 and get the roots.
26 : (d) ⇒ Degree = no: of zeros
27 : (c) ⇒ 3x−2 = 0 ⇒ x = 3/2 and y = 0
28 : (c) ⇒ Touches the x axis 3 times
29 : (a) ⇒ Definition of parabola
30 : (b) ⇒ Definition of parabola
31 :(c) ⇒ Definition of cubic polynomial
32 : (a) ⇒ Solve for sum of roots and product of roots
33 : (b) ⇒ Product of roots formula
34 : (a) ⇒ Solve x² − 11
35 : (b) ⇒ Use sum of zeroes formula
