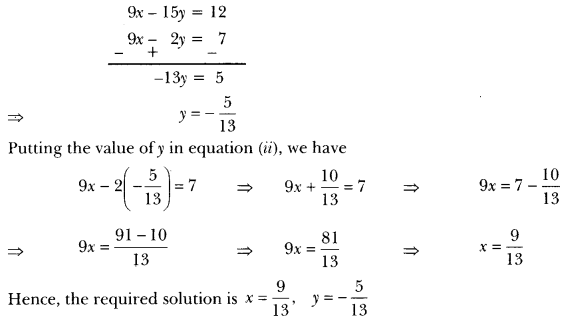ADDITIONAL QUESTIONS AND ANSWERS:

ADDITIONAL QUESTIONS AND ANSWERS:

1. If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then find value of  k.
Sol: Since the given lines are parallel

2) Find the value of c for which the pair of equations cx – y = 2 and
6x – 2y = 3 will have infinitely many solutions.

Sol: The given system of equations will have infinitely many solutions if 
c/6 = −1 /−2 = 2/3 which is not possible
∴ For no value of c, the given system of equations have infinitely many solutions.

3) Do the equations 4x + 3y – 1 = 5 and 12x + 9y = 15 represent a pair of coincident lines?
Sol:

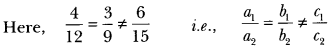
4) Given equations do not represent a pair of coincident lines.Find the
co-ordinate where  the  line  x – y = 8 will intersect y-axis.

Sol: The given line will intersect y axis when x = 0.
∴ 0 – y = 8    ⇒ y = −8
Required coordinate is (0, −8).

5) Write the number of solutions of the following pair of linear equations:
x + 2y – 8 = 0,   2x + 4y = 16
Sol:


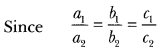
∴The given pair of linear equations has infinitely many solutions.

6) Is the following pair of linear equations consistent? Justify your answer.
2ax + by = a,    4ax + 2by – 2a = 0;     a, b ≠ 0
Sol:

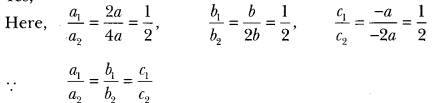
∴ Yes, the given system of equations is consistent.

7) For all real values of c, the pair of equations
x – 2y = 8,    5x + 10y = c
have a unique solution. Justify whether it is true or false.
Sol:

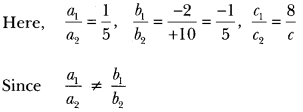
So, for all real values of c, the given pair of equations have a unique solution.
∴ The given statement is true.

8) Does the following pair of equations represent a pair of coincident lines? Justify your answer.
x/2 + y + 2/5 = 0,   4x+ 8y + 5/16 = 0.
Sol:

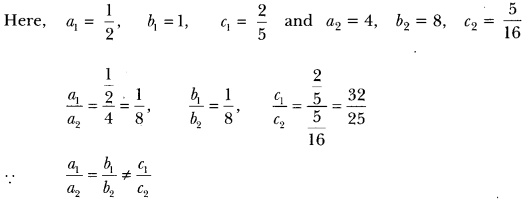
∴ The given system does not represent a pair of coincident lines.

9) If  x = a,   y = b is the solution of the pair of equation x – y = 2 
and  x + y = 4,then find the value of a and b.
Sol:
x – y = 2     … (i)
x + y = 4    … (ii)
On adding (i) and (ii), we get 2x = 6  or  x = 3
From  (i), 3 – y ⇒ 2 = y = 1
a = 3 ,  b = 1.
10) On comparing the ratios a₁/ a₂ , b₁ / b₂, and, c₁/c₂  find out whether the following pair of linear equations  is consistent or inconsistent.
3/2 x + 5/3 y = 7
 9x – 10y = 14
Sol:

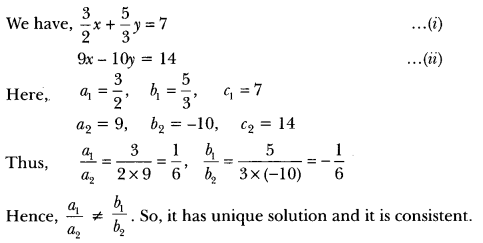
11) On comparing the ratios a1/a2 ,b1/b2, and c1/c2, find out whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident:

  i)     5x – 4y + 8 = 0
          7x + 6y – 9 = 0
Sol:

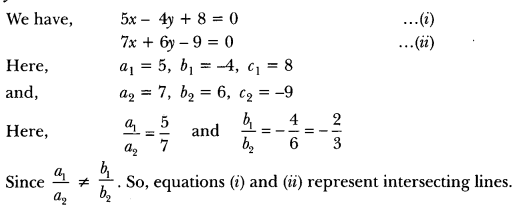
ii)   9x + 3y + 12 = 0
      18x + 6y + 24 = 0
Sol:
We have,
9x + 3y + 12 = 0
18x + 6y + 24 = 0

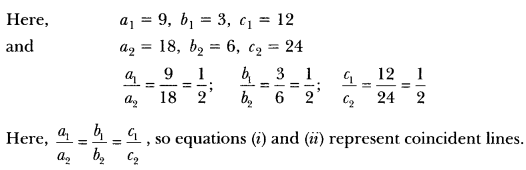
12) Solve: ax + by = a – b and bx – ay = a + b
Sol:  The given system of equations may be written as
ax + by – (a – b) = 0
bx – ay – (a + b) = 0
By cross-multiplication, we have

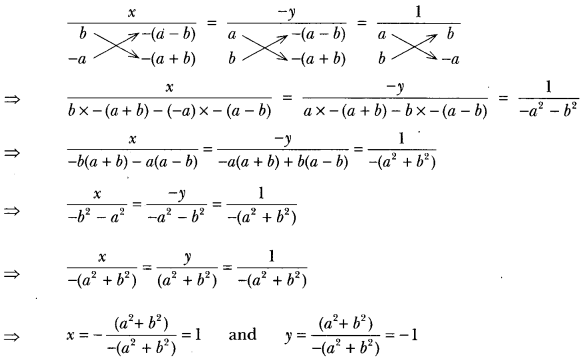
Hence, the solution of the given system of equations is x = 1, y = −1

13) Solve the following linear equations:
             152x – 378y = −74
and   −378x + 152y = −604
Sol:  We have, 152x – 378y  = −74                 …(i)
               − 378x + 152y  = −604             …(ii)

Putting the value of x in (iii), we get
2 + y = 3 ⇒ y = 1
Hence, the solution of given system of equations is x = 2, y = 1.

(14) For which values of a and b does the following pair of linear equations have an infinite number of solutions?   
2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
Sol:  We have, 2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2 … (ii)

Here, a₁ = 2, b₁ = 3, c₁ = 7 and
a2 = a – b,   b2 = a + b,   c2 = 3a + b – 2
For infinite number of solutions, we have

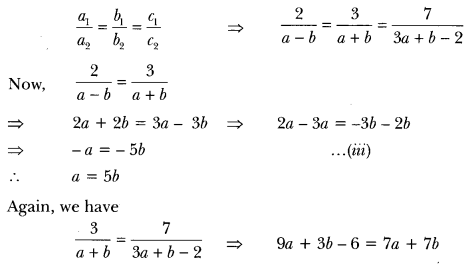
⇒ 9a – 7a + 3b – 75 −6 = 0 ⇒ 2a – 45 – 6 = 0 => 2a – 4b = 6

⇒ a – 2b = 3 …….. (iv)
Putting a = 5b in equation (iv), we get
56 – 2b = 3 or 3b = 3  i.e., b = 33 =1
Putting the value of b in equation (ii), we get a = 5(1) = 5
Hence, the given system of equations will have an infinite number of solutions
for a = 5 and b = 1.

(15) For which value of k will the following pair of linear equations have no solution?
3x + y = 1
(2k – 1) x + (k – 1) y = 2k + 1
Sol:  We have, 3x + y = 1 ,     3x + y − 1 = 0 …(i)
(2k – 1) x + (k – 1) y = 2k + 1
⇒ (2k – 1) x + (k – 1) y – (2k + 1) = 0 ……(ii)
Here, a₁ = 3 ,    b₁ = 1,   c₁ = −1
a2 = 2k – 1,   b2 = k – 1,   c2 = −(2k + 1)
For no solution, we must have

 

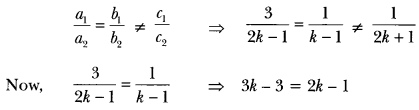
⇒ 3k – 2k = 3 – 1 ⇒ k = 2
Hence, the given system of equations will have no solution for k = 2.

16) Find whether the following pair of linear equations has a unique solution. If yes, find them
7x – 4y = 49  and  5x – y = 57
Sol:  We have, 7x – 4y = 49 ……..(i)
and 5x – 6y = 57 ……..(ii)

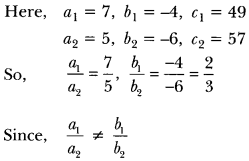
So, the system has a unique solution.
Multiply equation (i) by 5 and equation (ii) by 7 and subtract

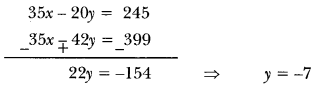
Put  y = −7 in equation (ii)

Put y = −7 in equation (ii)
5x – 6(−7)57   ⇒  5x = 57 – 42  ⇒  x = 3
Hence, x = 3 and y = −7.

17)  Solve for x and y.

Sol:

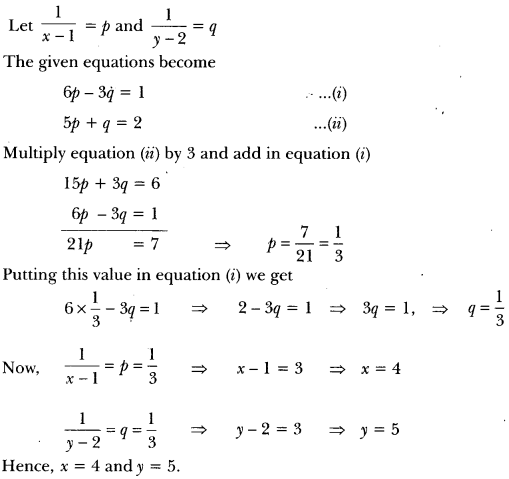
18) In Fig. 3.1, ABCDE is a pentagon with BE|CD and BC||DE. BC is perpendicular to CD. If the perimeter of ABCDE is 21 cm. Find the value of x and y.

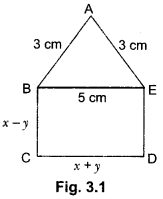
Sol:  Since BC||DE and BE||CD with BC||CD.
BCDE is a rectangle.
Opposite sides are equal BE = CD
∴ x + y = 5 …… (i)
DE = BC = x – y
Since perimeter of ABCDE  is 21 cm.
AB + BC + CD + DE + EA = 21
3 + x – y + x + y + x – y + 3 = 21 ⇒ 6 + 3x – y = 21

3x – y = 15 ….. (iii)
Adding (i) and (ii), we get
4x = 20 ⇒ x = 5
On putting the value of x in (i), we get y = 0
Hence, x = 5 and y = 0.

19) Five years ago, A was thrice as old as B and ten years later, A shall be twice as old as B. What are the present ages of A and B?
Sol:  Let the present ages of B and A be x years and y years respectively. Then
B’s age 5 years ago = (x – 5) years
and A’s age 5 years ago = (− 5) years
(−5) = 3 (x – 5) = 3x – y = 10 …….(i)
B’s age 10 years hence = (x + 10) years
A’s age 10 years hence = (y + 10) years
y + 10 = 2 (x + 10) = 2x – y = −10 …….. (ii)
On subtracting (ii) from (i) we get x = 20
Putting x = 20 in (i) we get
(3 × 20) – y = 10 ⇒ y = 50
∴ x = 20 and y = 50
Hence, B’s present age = 20 years and A’s present age = 50 years.

20) A fraction becomes 1/3 when 1 is subtracted from the numerator and becomes 1/4 when 8 is added to its denominator. Find the fraction.
Sol:  Let the numerator be x and denominator be y.

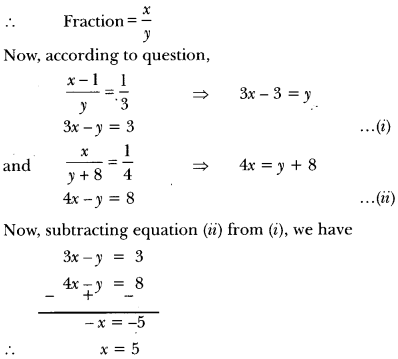
Putting the value of x in equation (i), we have
3 × 5 – y = 3 ⇒ 5 – y = 3 ⇒ 15 – 3 = y
∴ y = 12
Hence, the required fraction is 5/12

21) Form the pair of linear equations in this problem, and find its solution graphically: 10 students of Class X took part in a Mathematics quiz.
If the number of girls is 4 more than the number of boys,
find the number of boys and girls who took part in the quiz.
Sol:  Let x be the number of girls and y be the number of boys.
According to question, we have
x = y + 4
⇒ x – y = 4 ……(i)
Again, total number of students = 10
Therefore, x + y = 10 …(ii)
Hence, we have following system of equations
x – y = 4
and x + y = 10
From equation (i), we have the following table:

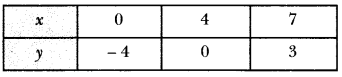
From equation (ii), we have the following table:

Plotting this, we have

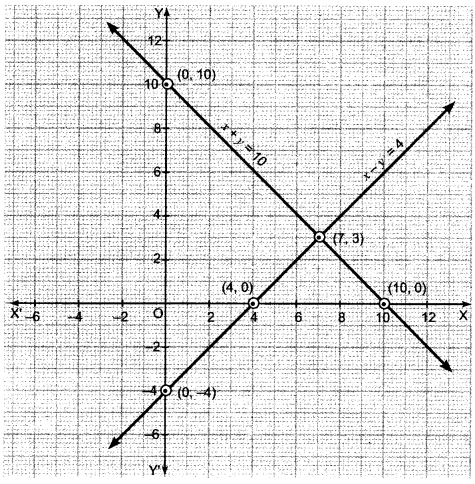
Here, the two lines intersect at point (7 , 3)    ⇒ x = 7,    y = 3.
So, the number of girls = 7
and number of boys = 3.

22) Show graphically the given system of equations
         2x + 4y = 10 and 3x + 6y = 12   has no solution.
Sol:  We have, 2x + 4y = 10
⇒ 4y = 10 – 2x ⇒ y = (5−x)/2
Thus, we have the following table:

Plot the points A (1, 2), B (3, 1) and C (5,0) on the graph paper. Join A, B and C and extend it on both sides to obtain the graph of the equation 2x + 4y = 10.
We have, 3x + 6y = 12

⇒ 6y = 12 – 3x ⇒ y = (4−x)/2
Thus, we have the following table :

Plot the points D (2, 1), E (0, 2) and F (4,0) on the same graph paper. Join D, E and F and extend it on both sides to obtain the graph of the equation 3x + 6y = 12.

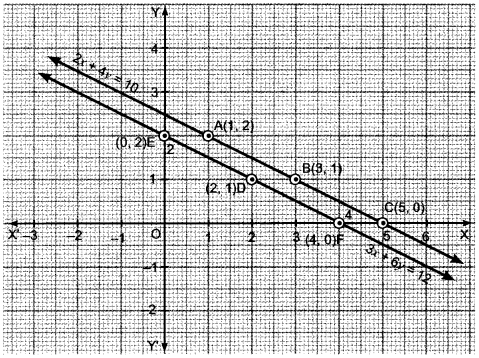
We find that the lines represented by equations 2x + 4y = 10 and 3x + y = 12 are parallel. So, the two lines have no common point. Hence, the given system.of equations has no solution.

23) Solve the following pairs of linear equations by the elimination method:
          3x – 5y – 4 = 0   and  9x = 2y + 7
Sol:  We have, 3x – 5y – 4 = 0
⇒ 3x – 5y = 4 …….(i)
Again, 9x = 2y + 7
9x – 2y = 7 …(ii)
Multiplying equation (i) by 3, we get
9x – 15y = 12 … (iii)
Subtracting (ii) from (iii), we get