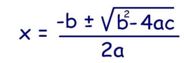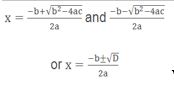3. Quadratic formula method:
In this method, we can find the roots by using quadratic formula. The quadratic formula is
where a, b and c are the real numbers and – 4ac is called discriminant.To find the roots of the equation, put the value of a, b and c in the quadratic formula.
Nature of Roots:
From the quadratic formula, we can see that the two roots of the Quadratic Equation are –
Where D = b2 – 4ac. The nature of the roots of the equation depends upon the value of D, so it is called the discriminant.
Example 1 : Solve Q. 2(i) of Exercise 4.1 by using the quadratic formula.
Solution:
Example 1 : Find the discriminant of the quadratic equation 2x²– 4x + 3 = 0, and hence find the nature of its roots.
Solution: : The given equation is of the form ax² + bx + c = 0, where a = 2, b = – 4 and c = 3. Therefore, the discriminant
b2 – 4ac = (– 4)2 – (4 × 2 × 3) = 16 – 24 = – 8 < 0
So, the given equation has no real roots.
Example 2 : Find two consecutive odd positive integers, sum of whose squares is 290.
Solution: Let one of the odd positive integer be x
then the other odd positive integer is x + 2
their sum of squares = x² + (x + 2)²
= x² + x² + 4x +4
= 2x² + 4x + 4
Given that their sum of squares = 290
⇒ 2x² + 4x + 4 = 290
⇒ 2x² + 4x = 2904 = 286
⇒ 2x² + 4x −286 = 0
⇒ 2 (x² + 2x −143) = 0
⇒ x² + 2x −143 = 0
⇒ x² + 13x −11x −143 = 0
⇒ x (x + 13) 11 ( x + 13) = 0
⇒ (x −11) = 0 , (x + 13) = 0
Therefore , x = 11 or −13
We always take positive value of x
So , x = 11 and (x + 2) = 11 + 2 = 13
Therefore , the odd positive integers are 11 and 13 .
Example 3 : A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m (see Fig. 4.3). Find its length and breadth.
Solution: Let the length be l
therefore breadth = l −3
area = l (l −3)
the area of isosceles triangle = ½ × (l −3) x 12 = 6(l −3)
But it is given
⇒ l (l −3) −4 = 6 (l −3)
⇒ l² −3l −4 = 6l −18
⇒ l² −9l + 14 = 0
⇒ l² −2l −7l + 14 = 0
⇒ l (l −7) −2(l −7) = 0
⇒ (l −2) (l −7) = 0
⇒ l = 7 or 2 and the breadth is 4
since breadth cannot be negative.
Example 4 : A motor boat whose speed is 18 km/h in still water takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Solution: The speed of the motor boat in still water is 18 kmph, it takes 1 hour to travel upstream & return to same spot.
⇒ The speed of motor boat (boat’s engine) = 18 kmph ,
⇒ It travelled 24 km upstream & 24 km downstream in 1 hour.
We have to find the speed of the stream .
Time = Distance/Speed
So,let the speed of stream be x. Then,we can say that,
24/(18 −x) −24/(18 + x) = 1 …..(i) (All the units are in hour km per hour,etc,.)
(24 (18+ x) −24(18 −x))/((18 − x) (18 + x)) = 1
(24 (18 + x) −24(18 −x))/ [(18 −x) (18 + x)] = 1
24 (2x)/(324 −x²) = 1
⇒ 324 −x² = 48 x
⇒ x² −48x + 324 = 0
⇒ x² + 48x −324 = 0
⇒ x² −6x + 54x −324 = 0
⇒ x (x −6) + 54(x −6) = 0
⇒ (x + 54)(x −6) = 0
For the equation to be 0,
Either, x + 54 = 0 (or) x − 6 = 0
⇒ x = −54 (or) x = 6
⇒ x = 6 (As speed can’t be negative, x ≠ −54.
∴ The speed of the stream is 6 kmph
EXERCISE 4.4
1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them.
Solution: (i) 2x2 – 3x + 5 = 0
Comparing the equation with ax² + bx + c = 0, we get
a = 2, b = −3 and c = 5
We know, Discriminant = b² – 4ac
= ( – 3)2– 4 (2) (5) = 9 – 40
= – 31
As you can see, b² – 4ac < 0
Therefore, no real root is possible for the given equation, 2x² – 3x + 5 = 0.
(ii) 3x2 – 4√3x + 4 = 0
Comparing the equation with ax² + bx + c = 0, we get
a = 3, b = −4√3 and c = 4
We know, Discriminant = b² – 4ac
= (4√3)2 – 4(3)(4)
= 48 – 48 = 0
As b² – 4ac = 0,
Real roots exist for the given equation and they are equal to each other.
Hence the roots will be –b/2a and –b/2a.
–b/2a = (4√3)/2 × 3 = 4√3/6 = 2√3/3 = 2/√3
Therefore, the roots are 2/√3 and 2/√3.
(iii) 2x² – 6x + 3 = 0
Comparing the equation with ax² + bx + c = 0, we get
a = 2, b = 6, c = 3
As we know, Discriminant = b² – 4ac
= (6)² – 4 (2) (3)
= 36 – 24 = 12
As b² – 4ac > 0,
Therefore, there are distinct real roots exist for this equation, 2x² – 6x + 3 = 0.
= [(−6) ± √(6² −4(2)(3) ]/ 2(2)
= (6 ± 2√3 )/4
= (3 ± √3)/2
Therefore the roots for the given equation are (3 + √3)/2 and (3 −√3)/2
2. Find the value of k for each of the following quadratic equations, so that they have two equal roots.
(i) 2x² + kx + 3 = 0
(ii) kx (x – 2) + 6 = 0
Solutions: (i) 2x² + kx + 3 = 0
Comparing the given equation with ax² + bx + c = 0, we get,
a = 2, b = k and c = 3
As we know, Discriminant = b² – 4ac
= (k)2 – 4(2) (3)
= k2 – 24
For equal roots, we know, Discriminant = 0
k2 – 24 = 0
k2 = 24
k = ±√24 = ±2√6
(ii) kx (x – 2) + 6 = 0
or kx² – 2kx + 6 = 0
Comparing the given equation with ax² + bx + c = 0, we get
a = k, b = – 2k and c = 6
We know, Discriminant = b² – 4ac
= ( – 2k)² – 4 (k) (6)
= 4k² – 24k
For equal roots, we know,
b2 – 4ac = 0
4k2 – 24k = 0
4k (k – 6) = 0
Either 4k = 0 or k = 6 = 0
k = 0 or k = 6
However, if k = 0, then the equation will not have the terms ‘x2‘ and ‘x‘.
Therefore, if this equation has two equal roots, k should be 6 only.
3. Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m². If so, find its length and breadth.
Solution: Let the breadth of mango grove be l.
Length of mango grove will be 2l.
Area of mango grove = (2l) (l) = 2l²
2l2 = 800
l2 = 800/2 = 400
l2 – 400 =0
Comparing the given equation with ax² + bx + c = 0, we get
a = 1, b = 0, c = 400
As we know, Discriminant = b² – 4ac
=> (0)² – 4 × (1) × ( – 400) = 1600
Here, b² – 4ac > 0
Thus, the equation will have real roots. And hence, the desired rectangular mango grove can be designed.
l = ± 20
As we know, the value of length cannot be negative.
Therefore, breadth of mango grove = 20 m
Length of mango grove = 2 × 20 = 40 m
4. Is the following situation possible? If so, determine their present ages.The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution: Let’s say, the age of one friend be x years.
Then, the age of the other friend will be (20 – x) years.
Four years ago,
Age of First friend = (x – 4) years
Age of Second friend = (20 – x – 4) = (16 – x) years
As per the given question, we can write,
(x – 4) (16 – x) = 48
16x – x² – 64 + 4x = 48
– x² + 20x – 112 = 0
x² – 20x + 112 = 0
Comparing the equation with ax² + bx + c = 0, we get
a = 1, b = 20 and c = 112
Discriminant = b² – 4ac
= (20)² – 4 × 112
= 400 – 448 = 48
b² – 4ac < 0
There will be no real solution possible for the equations. Hence, condition doesn’t exist.
5. Is it possible to design a rectangular park of perimeter 80 metres and area 400 m². If so, find its length and breadth.
Solution: Let the length and breadth of the park be l and b.
Perimeter of the rectangular park = 2 (l + b) = 80
So, l + b = 40
Or, b = 40 – l
Area of the rectangular park = l × b = l (40 – l) = 40l – l² = 400
l² – 40l + 400 = 0, which is a quadratic equation.
Comparing the equation with ax² + bx + c = 0, we get
a = l, b = 40, c = 400
Since, Discriminant = b² – 4ac
= (40)² – (4 × 1 x 400)
= 1600 – 1600 = 0
Thus, b² – 4ac = 0
Therefore, this equation has equal real roots. Hence, the situation is possible.
Root of the equation,
l = –b/2a
l = (40)/2(1) = 40/2 = 20
Therefore, length of rectangular park, l = 20 m
And breadth of the park, b = 40 – l = 40 – 20 = 20 m.
Additional Questions:
1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them.
2. Find the value of k for each of the following quadratic equations, so that they have two equal roots.
3. Is it possible to design a rectangular park of perimeter 100 metres and area 600 m2. If so, find its length and breadth.
4. Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 40 years. Four years ago, the product of their ages in years was 320.