AREAS OF SIMILAR TRIANGLES:
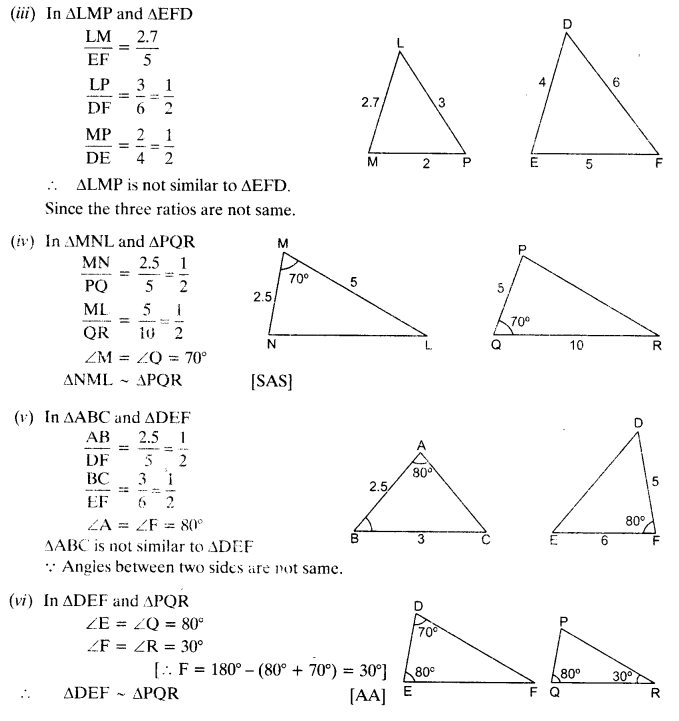
1) State which pairs of triangles in the given figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :


Solution:

2) In the given figure, ∆ODC ~ ∆OBA, ∠BOC = 125° and ∠CDO = 70°.
Find ∠DOC, ∠DCO and ∠OAB.

Solution:

3) Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that OA/OC = OB/OD
Solution:

4). In the given figure QR/QS = QT/PR and ∠1 = ∠2. Show that ΔPQS∼ΔTQR

Solution:


5) S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS. Show that ∆RPQ ~ ∆RTS.
Solution:

6) In the given figure, if ∆ABE ≅ ∆ACD, show that ∆ADE ~ ∆ABC.
Solution:

7) In the given figure, altitudes AD and CE of ∆ABC intersect each other at the point P. Show that:
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC
Solution:
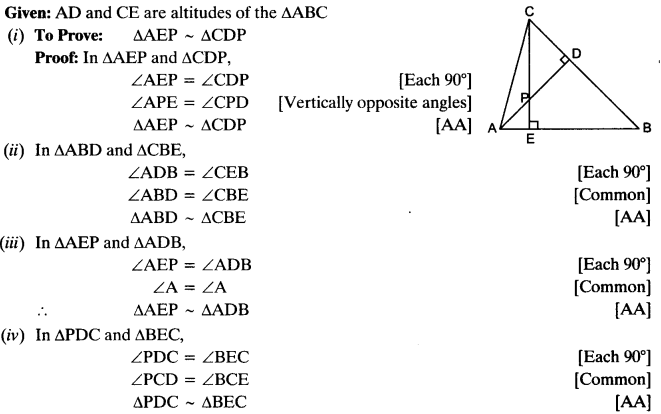
8) E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ABE ~ ∆CFB.
Solution:

9) In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:(i) ΔABC ∼ ΔAMP (ii) CA/PA = BC/MP

Solution:

10) CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG, show that
(i)CD/GH = AC/FG (ii) ΔDCB ∼ ΔHGE (iii) ΔDCA ∼ ΔHGF
Solution:


11) In the given figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ∆ABD ~ ∆ECF.
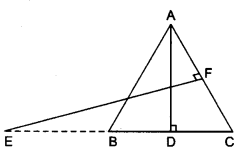
Solution:

12) Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆PQR (see in given figure). Show that ∆ABC ~ ∆PQR.
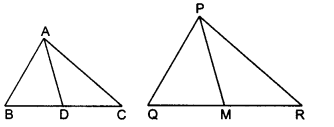
Solution:

13) D is a point on the side BC of a triangle ABC, such that ∠ADC = ∠BAC. Show that CA² = CB.CD.
Solution:

14) Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆PQR.
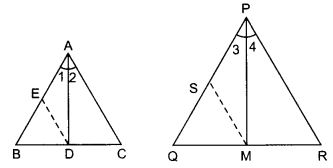
Solution:

15) A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:

DE is a vertical pole of length = 6 m
Length of its shadow = 4 m
Let height of tower AB = h m
Length of its shadow = 28 m
In ∆ABC and ∆DEC,
∠ABC = ∠DEC [Each 90°]
∠C = ∠C [Common]
∆ABC ~ ∆DEC [AA]
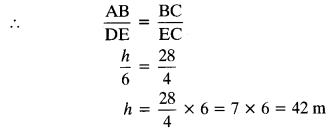
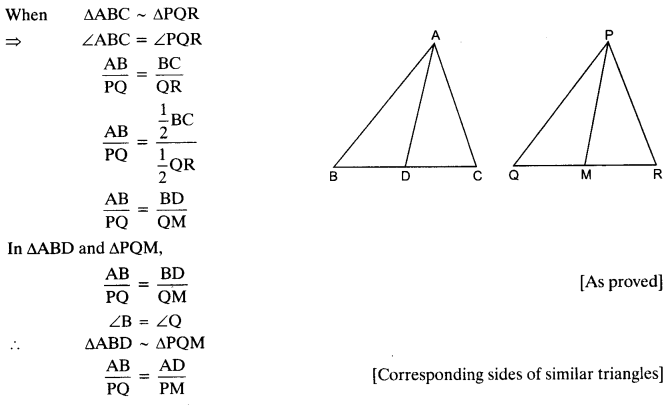
16) If AD and PM are medians of triangles ABC and PQR respectively, where
ΔABC ∼ ΔPQR. Prove that AB/PQ = AD/PM
Solution: