ADDITIONAL QUESTIONS AND ANSWERS:
1) What is the area of the triangle formed by the points 0 (0, 0), A (−3, 0) and B (5, 0)?
Sol:
Area of ∆OAB = 12 [0(0 – 1) – 3(0 – 0) + 5(0 – 0)] = 0
⇒ Given points are collinear. So a triangle cannot be formed.
2) If the centroid of triangle formed by points P (a, b), Q (b, c) and R (c, a) is at the origin, what is the value of a + b + c.
Sol:
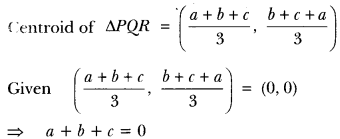
3). AOBC is a rectangle whose three vertices are A (0, 3), O (0, 0) and B (5, 0). Find the length of its diagonal.
Sol:
![]()
4) Find the value of a, so that the point (3, a) lie on the line 2x – 3y = 5.
Sol: Since (3, a) lies on the line 2x – 3y = 5
Then 2(3) – 3(a) = 5
– 3a = 5 – 6
– 3a = −1
⇒ a = 13
5) Find distance between the points (0, 5) and (−5, 0).
Sol: Here x1 = 0, y1 = 5, x2 = −5 and y2 = 0
![]()
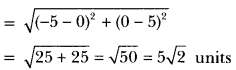
6) Find the distance of the point (−6,8) from the origin.
Sol: Here x1 = −6, y1 = 8
x2 = 0, y2 = 0
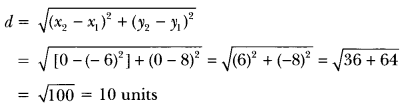
7) If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?
Sol: Using distance formula
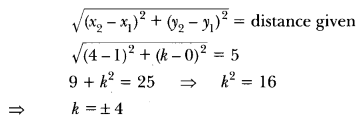
8) If the points A (1, 2), B (0, 0) and C (a, b) are collinear, then what is the relation between a and b?
Sol: Points A, B and C are collinear
⇒ 1(0 – b) + 0 (b – 2) + a(2 – 0) = 0
⇒ −b + 2a = 0 ⇒ 2a = b
9) Find the ratio in which the line segment joining the points (−3, 10) and (6, – 8) is divided by (−1, 6).
Sol: In Fig. 6.6, let the point P(−1, 6) divides the line joining
A(−3, 10) and B (6, −8) in the ratio k : 1

Hence, the point P divides AB in the ratio 2 : 7
10) Write the coordinates of a point on x-axis which is equidistant from the points (−3, 4) and (2, 5).
Sol: Let the required point be (x, 0).
Since, (x, 0) is equidistant from the points (−3, 4) and (2, 5) .
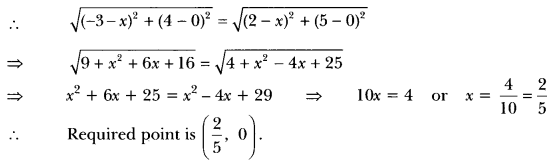
11) Find the values of x for which the distance between the points P (2, −3) and Q (x, 5) is 10.
Sol:
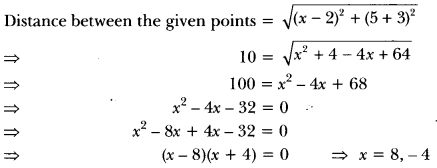
12) In Fig. 6.8, if A(−1, 3), B(1, −1) and C (5, 1) are the vertices of a triangle ABC, what is the length of the median through vertex A?
Sol:
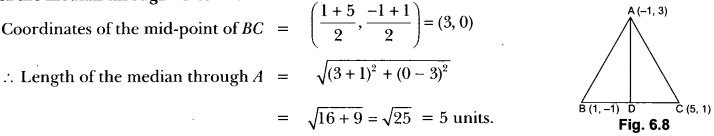
13) Show that ∆ABC, where A (−2, 0), B (2, 0), C(0, 2) and ΔPQR where P(−4, 0), Q(4, 0), R(0, 4) are similar triangles.
Sol:
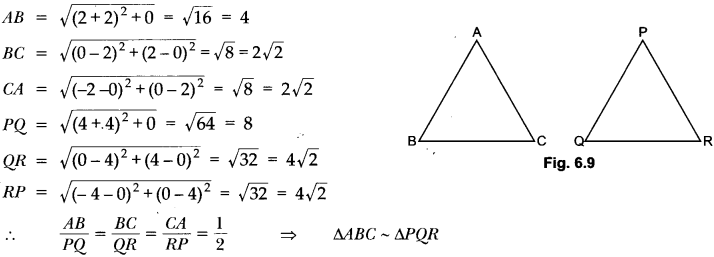
14) Point P (0, 2) is the point of intersection of y-axis and perpendicular bisector of line segment joining the points, A (−1, 1) and B (3, 3). State true or false and justify your answer.
Sol: The point P (0, 2) lies on y axis
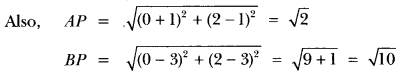
AP ≠ BP
∴ P(0, 2) does not lie on the perpendicular bisector of AB. So, given statement is false.
15) Check whether (5, −2), (6, 4) and (7, −2) are the vertices of an isosceles triangle.
Sol: Let A (5,−2), B (6, 4) and C (7, −2) be the vertices of a triangle
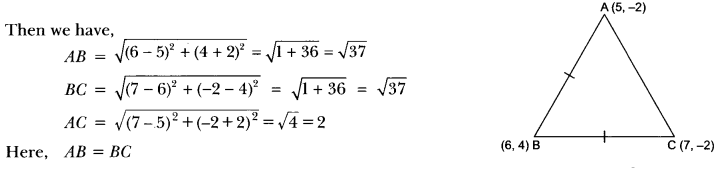
Here, AB = BC
∴ ∆ABC is an isosceles triangle.
16) If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Sol: Let A (1, 2), B (4, y), C (x, 6) and D (3, 5) be the vertices of a parallelogram ABCD.
Since, the diagonals of a parallelogram bisect each other.
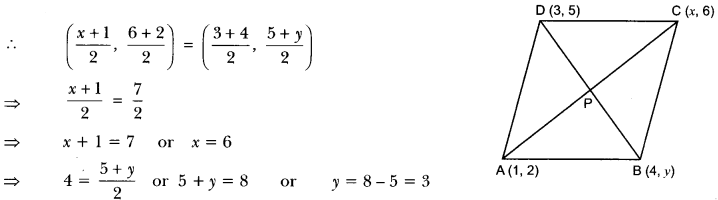
Hence, x = 6 and y = 3.
17) Let P and Q be the points of trisection of the line segment joining the points A (2, −2) and B (−7, 4) such that P is nearer to A. Find the coordinates of P and Q.
Sol:
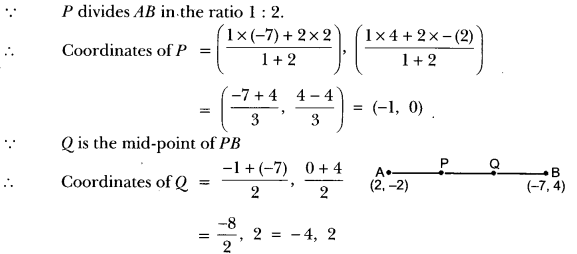
18) The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q (2, −5) and R (−3, 6), find the coordinates of P.
Sol: Let the point P be (2y, y)
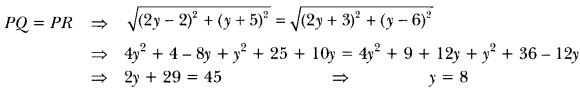
Hence, coordinates of point P are (16, 8).
19) Determine, if the points (1, 5), (2, 3) and (−2, −11) are collinear.
Sol: Let A (1, 5), B (2, 3) and C (−2, −11) be the given points. Then we have
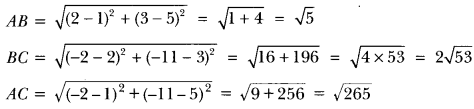
Clearly, AB + BC ≠ AC
∴ A, B, C are not collinear.
20) Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (−1, −2), (1, 0), (− 1, 2), (−3, 0)
Sol: Let A (−1, −2), B (1, 0), C (−1, 2) and D (−3, 0) be the four given points.
Then, using distance formula, we have,
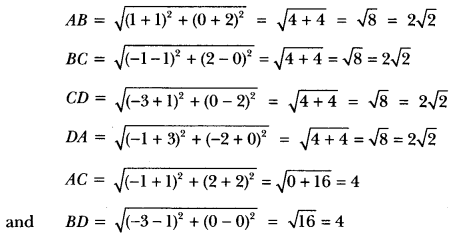
Here, four sides of quadrilateral are equal and diagonals AC and BD are also equal.
∴ Quadrilateral ABCD is a square.
21) If Q (0, 1) is equidistant from P (5,−3) and R (x, 6) find the value of x. Also, find the distances of QR and PR.
Sol: Since, point Q (0, 1) is equidistant from P (5, −3) and R (x, 6).
Therefore, QP = QR
Squaring both sides, we have, QP2 = QR2
⇒ (5 – 0)2 + (−3 −1)2 = (x – 0)2 + (6 – 1)2
25 + 16 = x2 + 25
x2 = 16
∴ x = ±4
Thus, R is (4, 6) or (−4, 6).
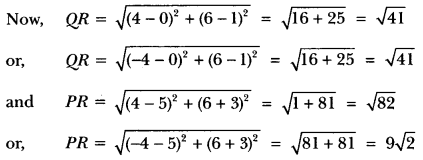
22) Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (−3, 4).
Sol: Let P(x, y) be equidistant from the points A( 3, 6) and B(−3, 4)
i.e., PA = PB
Squaring both sides, we get
AP2 = BP2
⇒ (x – 3)2 + (y – 6)2 = (x + 3)2 + (1 – 4)2
⇒ x2 – 6x + 9 + y2 – 12y + 36 = x2 + 6x + 9 +y2 – 8y + 16
⇒ -12x – 4y + 20 = 0
⇒ 3x + y – 5 = 0, which is the required relation.
Let A (1, 5), B (2, 3) and C (−2, −11) be the given points. Then we have
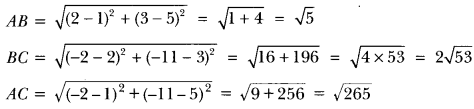
Clearly, AB + BC ≠ AC
∴ A, B, C are not collinear.
24. Find the distance between the following pairs of points:
(i) (-5, 7), (-1, 3)
(ii) (a, b), (-a, -b)
Sol:
(i) Let two given points be A (-5, 7) and B (-1, 3).
Thus, we have x1 = -5 and x2 = -1
y1 = 7 and y2 = 3
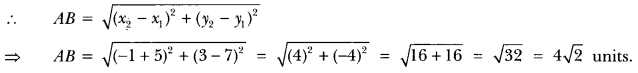
(ii) Let two given points be A (a,b) and B(-a, -b)
Here, x1 = a and x2 = -a; y1 = b and y2 = -b
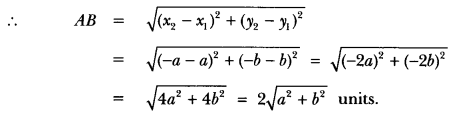
25. A line segment is of length 10 units. If the coordinates of its one end are (2, -3) and the abscissa of the other end is 10, find its ordinate.
Sol:
We have, PQ = 10
![]()
Squaring both sides, we have
⇒ (8)2 + (y + 3)2 = 100
⇒ (y + 3)2 = 100 – 64
⇒ (y + 3)2 = 36 or y + 3 ± 16
⇒ y + 3 = 6, y + 3 = -6 or y = 3, y = -9
Hence, values of y are – 9 and 3.
26. Find the relation between x and y, if the points (x, y), (1, 2) and (7, 0) are collinear.
Sol:
Given points are A (x, y), B (1, 2) and C (7, 0)
These points will be collinear if the area of the triangle formed by them is zero.
Now, ar (∆ABC) = 12 [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
⇒ 0 = 12 [x(2 – 0) + 1(0 – y) + 7(y – 2)]
⇒ 0 = 12 (2x – y + 7y – 14)
⇒ 2x + by – 14 = 0
⇒ x + 3y = 7, which is the required relation between x and y.
27. Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
Sol:
Let the coordinates of A be (x, y)
Now, C is the centre of circle therefore, the coordinates of
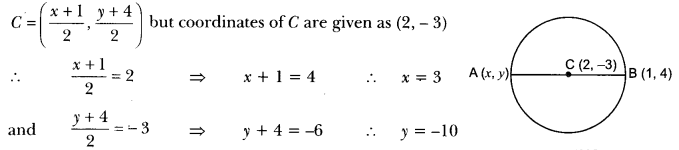
Hence, coordinates of A are (3, −10).
28. Find the area of the triangle whose vertices are: (−5, −1), (3, −5), (5, 2)
Sol:
Let A (x1, y1) = (−5, −1), B (x2, y2) = (3 – 5), C (x3, y3) = (5, 2)
∴ area of ∆ABC = 12 [x1 (y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= 12 [−5(−5 – 2) + 3 (2 + 1) + 5(−1 + 5)]
= 12(35 + 9 + 20) = 12 × 64 = 32 sq units.
29. If the point P(x, y) is equidistant from the points A(a + b, b – a) and B(a – b, a + b).
Prove that bx = ay.
Sol:
Given, PA = PB or (PA)2 = (PB)2
(a + b – x)2 + (b – a – y)2 = (a – b – x)2 + (a + b – y)2
⇒ (a + b)2 + x2 – 2ax – 25x + (b – a)2 + y2 – 2by + 2ay
⇒ (a – b)2 + x2 – 2ax + 2bx + (a + b)2 + y2 – 2ay – 2by
⇒ 4ay = 4bx or bx = ay
Hence proved.
30. Find the value of ‘k”, for which the points are collinear: (7, -2), (5, 1), (3, k).
Sol:
Let the given points be
A (x1, y1) = (7, -2), B (x2, y2) = (5, 1) and C (x3, y3) = (3, k)
Since these points are collinear therefore area (∆ABC) = 0
⇒ 12 [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 0
⇒ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) = 0
⇒ 7(1 – k) + 5(k + 2) + 3(-2 -1) = 0
⇒ 7 – 7k + 5k + 10 – 9 = 0
⇒ -2k + 8 = 0
⇒ 2k = 8
⇒ k = 4
Hence, given points are collinear for k = 4.
