INTRODUCTION:
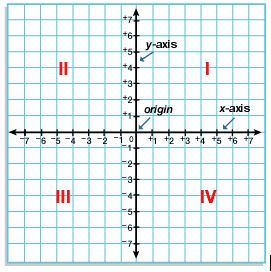
In the Cartesian coordinate system, there is a Cartesian plane which is made up of two number lines which are perpendicular to each other, i.e. x-axis (horizontal) and y-axis (vertical) which represents the two variables. These two perpendicular lines are called the coordinate axis.
• The intersection point of these two lines is known as the center or the origin of the coordinate plane. Its coordinates are (0, 0).
• Any point on this coordinate plane is represented by the ordered pair of numbers. Let (a, b) is an ordered pair then a is the x-coordinate and b is the y-coordinate.
• The distance of any point from the y-axis is called its x-coordinate or abscissa and the distance of any point from the x-axis is called its y-coordinate or ordinate.
• The Cartesian plane is divided into four quadrants I, II, III and IV.
Equation of a Straight Line:
An equation of line is used to plot the graph of the line on the Cartesian plane.
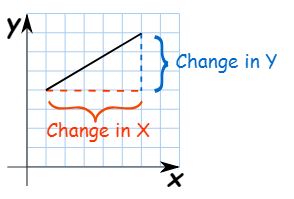
The equation of a line is written in slope intercept form as
y = mx +b where m is the slope of the line and b is the y intercept.
To find the slope of the line first we need to convert the equation in the slope intercept form then we can get the slope and y intercept easily.
The distance between P ( x1 , y1) and Q ( x2,y2) is =√(x2− x1 ) )2 + (y2 − y1 )2
The distance of a point P(x, y) from the origin is √(x2 + y2 ).
The coordinates of the point P(x, y) which divides the line segment joining the points
A (x1 ,y1 ) and B ( x2 ,y2 )) internally in the ratio m1 : m2 are (m1 x2 + m2 x1)/(m1 + m2 ) , (m1 y2+ m2 y1)/(m1 + m2 )
The mid-point of the line segment joining the points P ( x1, y1 ) and Q ( x2 ,y2 ) is
(x1 + x2)/2 , (y1 + y2)/2 .
The area of the triangle formed by the points ( x1 ,y 1) , ( x2, y2 )) and ( x3 ,y3 )) is the numerical value of the expression 1/2 [x2 (y2− y3 )+ x2 (y3 − y1 ) + x3 (y1 − y2)]