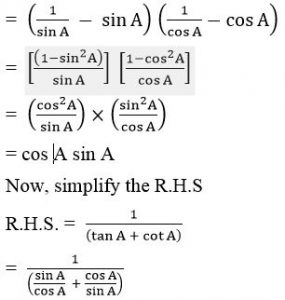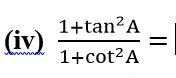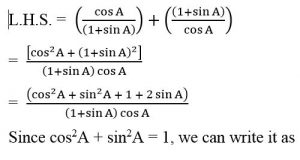EXERCISE 8.4

TRIGNOMETRIC IDENTITIES:  (Pythagoras Identity)

An equation is said to be a trigonometric identity if it contains trigonometric ratios of an angle and satisfies it for all values of the given trigonometric ratios.

 

Example 1 : Find the value of x in each of the following:

(i) cosec 3 x = (cot 30° + cot 60°)/(1 + cot 30° cot 60°)

(ii) cos x = 2 sin 45° cos 45° – sin 30°

(i) cosec 3 x = (cot 30° + cot 60°)/(1 + cot 30° cot 60°)

cot 30° = √3 ; cot 60° = 1/√3
(cot 30° + cot 60°)/(1 + cot 30° cot 60°)
= (√3 + 1/√3)/(1 + √3 × 1/√3)
= ( (3 + 1)/√3)/(2 )  ⇒  4/√3 × 1/2  ⇒ 2/√3
So, cosec 3x  =2/√3
But cosec 3x  = cosec 60°
∴ 3x  = 60°  ⇒   x = 20°

(ii) cos x  = 2 sin 45° cos 45° – sin 30°

 The values are  sin 45° = cos 45°= 1/√2 ;  sin 30° = 1/2
cos x = 2 sin 45° cos 45° – sin 30°= [ 2 × 1/√2 × 1/√2 ] −1/2
cos x = 1 −1/2  ⇒  1/2
We know cos 60° = 1/2                                                                                                                                           ∴ cos x = cos 60° or    x = 60°

Example 2 : If θ is an acute angle and (sinθ + 1 )/(sinθ − 1) = (√3 + 2)/(√3−2) , find θ. 

Divide both numerator and denominator of RHS by 2 :
[(√3 + 2)/2)/((√3−2)/2] = [ (√3 )/2 +1)/(√3/2 −1]
sin 60° = √3/2
[(√3 )/2 +1)/(√3/2 −1] = (sin 60° + 1)/(sin 60°− 1)
∴ sin θ = sin 60°
θ = 60°

Example 3 : Prove that (Cosec A)/(Cosec A−1) +(Cosec A)/(Cosec A+1) = 2 + 2 (tan)² A=2 (sec)² A

Solution: LHS = (Cosec A)/(Cosec A−1) +(Cosec A)/(Cosec A+1)

= [(Cosec A)] x [1/(Cosec A−1)+ 1/ (Cosec A+1) )]
= [CosecA ] x [1/(Cosec A−1)(Cosec A+1)]
= [Cosec A] x [ (Cosec A−1) + (Cosec A+1) / (Cosec A−1)(Cosec A+1) ]

= [Cosec A] x [ (Cosec A + (Cosec A) / (Cosec A−1)(Cosec A+1) ]
= [Cosec A] x [ (2Cosec A) / (Cosec A−1)(Cosec A+1) ]
=  [ (2Cosec² A) / [(Cosec A−1)(Cosec A+1) ]
=  [ (2Cosec² A) / (Cosec² A−1) 
=  [ (2Cosec² A) / (Cot²A ) 
=[ 2 (1 + Cot²A)] / (Cot²A ) 
=[ 2 (1 + Cot²A)] x Tan² A
=[ 2 [ (1 x Tan² A)+ (Cot²A x Tan² A)]
=[ 2 [ (Tan² A)+ 1]              (proved)
= 2 Sec² A  (proved)
= RHS.

EXERCISE 8.4

1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:
To convert the given trigonometric ratios in terms of cot functions, use trigonometric formulas
We know that,
 Cosec² A – cot² A = 1
Cosec² A = 1 + cot² A
Since cosec function is the inverse of sin function, it is written as
1/(sin² A)=1 + cot ² A
Now, rearrange the terms, it becomes
Sin² A = 1/(1+ cot² A)
Now, take square roots on both sides, we get
Sin A = (1)/(√(1 + cot² A) 
The above equation defines the sin function in terms of cot function.

Now, to express sec function in terms of cot function, use this formula
sin² A = 1/(1+ cot² A)
Now, represent the sin function as cos function                                                                                                   1 – cos² A = 1/(1+ cot² A)
Rearrange the terms,                                                                                                                                                  cos² A = 1 – 1/(1+ cot² A)  ⇒ cos² A = (1−1 + cot² A) /(1+ cot² A)
Since sec is the inverse of cos ,
⇒ 1/(sec² A)=(cot² A)/(1+cot² A) 
Take the reciprocal and square roots on both sides, we get
⇒ sec A = ±√ (1+ cot² A)/cot A
Now, to express tan function in terms of cot function                                                                                 
tan A = (sin A)/(cos A) and cot A = cos ⁡A/sin⁡ A
Since cot function is the inverse of tan function, it is rewritten as
tan A = 1/cot⁡ A

2.Write all the other trigonometric ratios of ∠A in terms of sec A.

Solution:   Cos A  in terms of sec A:
sec A = 1/cos⁡A
⇒ cos A = 1/sec⁡A
sin A  in terms of sec A:
cos²A + sin²A = 1
Rearrange the terms
sin²A = 1 – cos²A
sin²A = 1 – (1/(sec² A))
sin²A = ((sec² A−1))/(sec² A)
sin A = (√(sec² A−1))/sec⁡A
cosec A  in terms of sec A:
sin A = 1/(cosec A)
⇒ cosec A = 1/sin⁡A
cosec A =  sec⁡A/(√(sec² A−1) 

  tan A in terms of sec A:
sec²A – tan²A = 1
Rearrange the terms
⇒ tan²A = sec²A + 1
tan A = √(sec²A + 1)
cot A  in terms of sec A:
tan A = 1/cot⁡A
⇒ cot A = 1/tan⁡A
cot A =  1/(√(sec)² A + 1) 

3. Evaluate:
(i) [(sin² 63°+sin² 27°)]/[(cos² 17°+cos² 73°) ]

(ii) sin 25° cos 65° + cos 25° sin 65°

Solution:
(i) [sin² 63°+sin² 27°] / [cos² 17°+cos² 73° ]
To simplify this, convert some of the sin functions into cos functions and cos function into sin function and it becomes,
= [sin² (90°−27°) + sin² 27°] / [cos² (90°−73°) + cos² 73°]
= (cos²27°+ sin² 27°) / (sin 27° + cos² 73°) 
= 1/1 = 1 (since sin²A + cos²A = 1)
Therefore, (sin² 63°+ sin² 27°)/(cos² 17° + cos² 73°)  = 1

(ii) sin 25° cos 65° + cos 25° sin 65°
To simplify this, convert some of the sin functions into cos functions and cos function into sin function and it becomes,

= sin (90°−25°) cos 65° + cos (90°−65°) sin 65°
= cos 65° cos 65° + sin 65° sin 65°
= cos²65° + sin²65° = 1 (since sin²A + cos²A = 1)
Therefore, sin 25° cos 65° + cos 25° sin 65° = 1

4.Choose the correct option. Justify your choice.

(i) 9 sec²A – 9 tan²A =
(A) 1                 (B) 9              (C) 8                (D) 0

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
(A) 0                 (B) 1              (C) 2                (D) – 1

(iii) (sec A + tan A) (1 – sin A) =
(A) sec A           (B) sin A        (C) cosec A      (D) cos A

(A) sec² A                 (B) −1              (C) cot²A                (D) tan²A

Solution:

(i) (B) is correct.
Justification:  9 sec²A – 9 tan²A
= 9 (sec²A – tan²A)
= 9 × 1 = 9             (∵ sec² A – tan² A = 1)
Therefore, 9 sec²A – 9 tan²A = 9

(ii) (C) is correct
Justification:  (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
We know that, tan θ = sin⁡θ/cos⁡θ
sec θ = 1/cos⁡θ
cot θ = cos⁡θ/sin⁡θ
 

5.Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

L.H.S. = (cosec θ – cot θ)²
The above equation is in the form of (a−b)², and expand it
Since (a−b)² = a² + b² – 2ab
Here a = cosec θ and b = cot θ
= (cosec²θ + cot²θ – 2cosec θ cot θ)

Now, apply the corresponding inverse functions and equivalent ratios to simplify

 

Since secant function is the inverse function of cos function and it is written as

With the help of identity function, cosec²A = 1+cot²A, let us prove the above equation.

First divide the numerator and denominator of L.H.S. by cos A,

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan²A + cot²A                                                                   L.H.S. = (sin A + cosec A)² + (cos A + sec A)²
It is of the form (a + b)², expand it   (a + b)² = a² + b² +2ab                                                                                = (sin²A + cosec²A + 2 sin A cosec A) + (cos²A + sec²A + 2 cos A sec A)
= (sin²A + cos²A) + 2 sin A(1/sin⁡A ) + 2 cos A(1/cos⁡A ) + 1 + tan²A + 1 + cot²A
= 1 + 2 + 2 + 2 + tan²A + cot²A
= 7 + tan²A + cot²A = R.H.S.
Therefore, (sin A + cosec A)² + (cos A + sec A)² = 7 + tan²A + cot²A
Hence proved.

(ix) (cosec A – sin A) (sec A – cos A) = 1/((tan⁡A + cot⁡A ) )
First, find the simplified form of L.H.S
L.H.S. = (cosec A – sin A) (sec A – cos A)
Now, substitute the inverse and equivalent trigonometric ratio forms

solution: