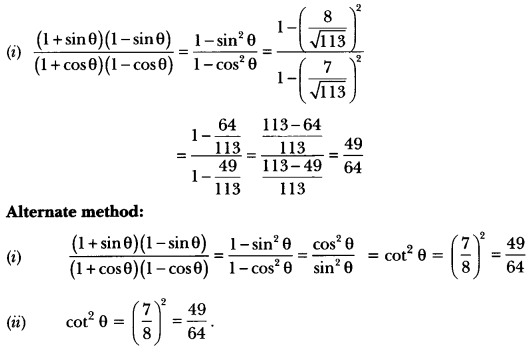ADDITIONAL QUESTIONS AND ANSWERS:

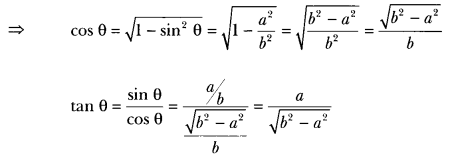
3) If sin (x – 20)° = cos (3x – 10)°, then find the value of x.
Sol:  sin (x – 20)° = cos (3x – 10)°
⇒ cos [90° – (x – 20)°] = cos (3x – 10)°
By comparing the coefficients
90° – x° + 20° = 3x° – 10° = 110° + 10° = 3x° + x°
120° = 4x°
⇒ x = 120°/4 = 30°

4) If x = a cos θ, y = b sin θ, then find the value of b²x² + a²y² – a²b².
Sol:  Given x = a cos θ, y = b sin θ
b²x² + a²y² – a²b² = b²(a cos θ)² + a²(b sin θ)² – a²b²
= a²b² cos²θ + a²b² sin² θ – a²b² = a²b² (sin² θ + cos² θ) – a²b²
= a²b² – a²b² = 0    (∵ sin² θ + cos² θ = 1)

5) If tan A = cot B, prove that A + B = 90°.
Sol:  We have tan A = cot B
⇒ tan A = tan (90° – B)
A = 90° – B
[∵ Both A and B are acute angles]
⇒ A + B = 90°

6) In a ∆ABC, if ∠C = 90°, prove that sin² A + sin² B = 1.
Sol:  Since ∠C = 90°
∴ ∠A + ∠B = 180° – ∠C = 90°
Now, sin² A + sin² B = sin² A + sin² (90° – A) = sin² A + cos² A = 1

7) If sec 4A = cosec (A – 20°) where 4 A is an acute angle, find the value of A.
Sol:  We have
sec 4 A = cosec (A – 20°)
⇒ cosec (90° – 4 A) = cosec (A – 20°)
∴ 90° – 4 A = A – 20°
⇒ 90° + 20° = A + 4 A
⇒ 110° = 5 A
⇒A = 22°

8) If sin A = 3/4, calculate cos A and tan A.
Sol:  Let us first draw a right ∆ABC in which ∠C = 90°.
Now, we know that

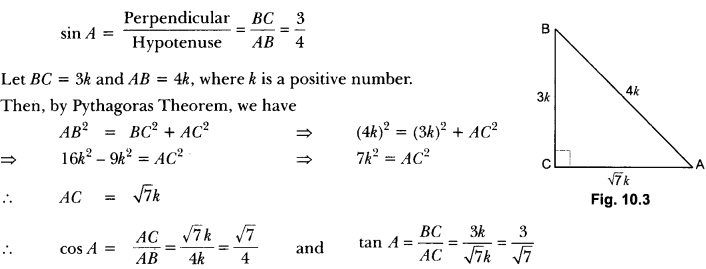
9) Given 15 cot A = 8, find sin A and sec A.
Sol:  Let us first draw a right ∆ABC in which ∠B = 90°.
Now, we have, 15 cot A = 8

10) In Fig. 10.5, find tan P – cot R.
Sol:

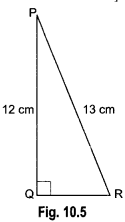
Using Pythagoras Theorem, we have
PR² = PO² + QR²
⇒ (13)² = (12)² + QR²
⇒ 169 = 144 + QR²
⇒ QR² = 169 – 144 = 25
⇒ QR = 5 cm
Now, tan P = QR/PQ = 5/12  and cot R = QR/PQ = 5/12
tan P −cot R = 5/12 − 5/12 = 0

11) Evaluate: sin 25° cos 65° + cos 25° sin 65°.
Sol: sin 25°. cos 65° + cos 25° . sin 65°
= sin (90° – 65°). cos 65° + cos (90° – 65°). sin 65°
= cos 65° . cos 65° + sin 65°. sin 65°
= cos² 65° + sin² 65° = 1.
  ∴ sin 25° cos 65° + cos 25° sin 65°= 1

12)If cosec θ = 13/12, evaluate 2sinθ − 3cosθ4sinθ − 9cosθ
Sol:

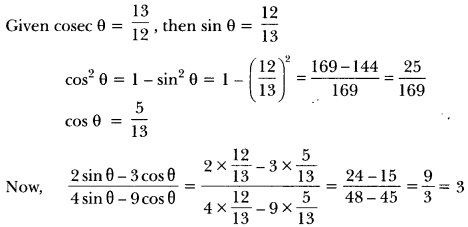
13) Prove that

Sol:

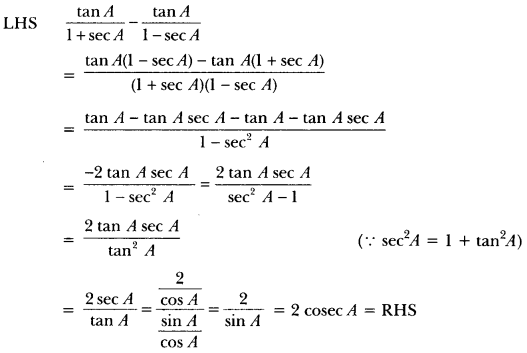
14) Prove that:

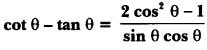
Sol:

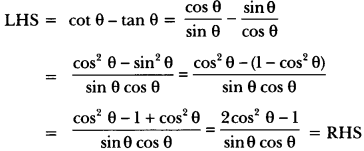
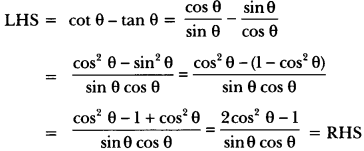
15) If tan (A +B) = √3 and tan (A – B) = √13; 0° < A + B ≤ 90°; A > B, find A and B.
Sol:
We have, tan (A + B) = √3
⇒ tan (A + B) = tan 60°
∴ A + B = 60°                 …(i)
Again, tan (A – B) = √13
∴ A – B = 30°               … (ii)
Adding (i) and (ii), we have
2A = 90°
⇒ A = 45°
Putting the value of A in (i), we have
45° + B = 60°
∴ B = 60° – 45° = 15°
Hence, A = 45° and B = 15°

16) Prove that: (cosec θ – cot θ)² = 1− cosθ/1 + cosθ
Sol:
LHS = (cosec θ – cot θ)²

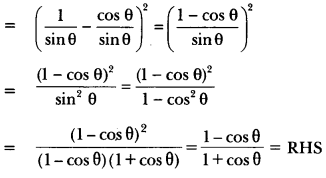
17) Prove that:

Sol:

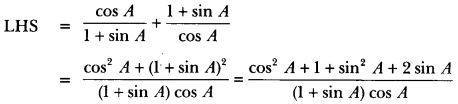
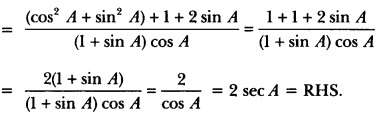
18) In ∆PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Sol:

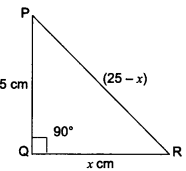
We have a right-angled ∆PQR in which ∠Q = 90°.
Let QR = x cm
Therefore, PR = (25 – x) cm
By Pythagoras Theorem, we have
PR² = PQ² + QR²
(25 – x)² = 5² + x²
= (25 – x)² – x² = 25
(25 – x – x) (25 – x + x) = 25
(25 – 2x) 25 = 25
25 – 2x = 1
25 – 1 = 2x
= 24 = 2x
∴ x = 12 cm
Hence, QR = 12 cm
PR = (25 – x) cm = 25 – 12 = 13 cm
PQ = 5 cm

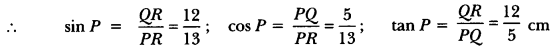
19) Prove that: (cosec A – sin A) (sec A – cos A) = 1/(tanA+cotA).
Sol:
LHS = (cosec A – sin A) (sec A – cos A)

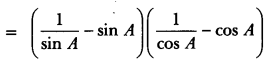
20) Prove that:

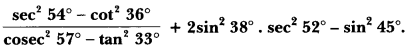
Sol:

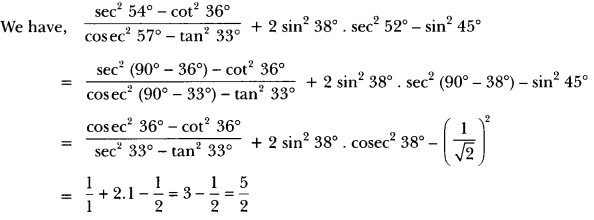
21). If sin (x – 20)° = cos (3x – 10)°, then find the value of x.
Sol:  sin (x – 20)° = cos (3x – 10)°
⇒ cos [90° – (x – 20)°] = cos (3x – 10)°
By comparing the coefficients
90° – x + 20° = 3x – 10° = 110° + 10° = 3x + x
120° = 4x
⇒ x = 30°

22). If tan A = cot B, prove that A + B = 90°.
Sol: We have tan A = cot B
⇒ tan A = tan (90° – B)
A = 90° – B
[∵ Both A and B are acute angles]
⇒ A + B = 90°

23). If sec 4A = cosec (A – 20°) where 4 A is an acute angle, find the value of A.
Sol:   We have
sec 4 A = cosec (A – 20°)
⇒ cosec (90° – 4 A) = cosec (A – 20°)
∴ 90° – 4 A = A – 20°
⇒ 90° + 20° = A + 4 A
⇒ 110° = 5 A
∴ A  = 22°

24). If sin θ + cos θ = √3 , then prove that tan θ + cot θ = 1.
Sol:   sin θ + cos θ = √3
⇒ (sin θ + cos θ)² = 3
⇒ sin² θ + cos² θ + 2 sin θ cos θ = 3
⇒ 2 sin cos θ = 2 (∵ sin² θ + cos² θ = 1)
⇒ sin θ. cos θ = 1 = sin² θ + cos² θ

⇒ 1 = tan θ + cot θ = 1
Therefore tan θ + cot θ = 1

25. Prove that: 2 sec θ – sec θ – 2 cosec θ + cosec θ = cot – tan θ.
Sol:
LHS = 2 sec θ – sec θ – 2 cosec² θ + cosec θ
= 2 (sec² θ) – (sec² θ)² – 2 (cosec² θ) + (cosec θ)²
= 2 (1 + tan² θ) – (1 + tan⁴ θ)² – 2(1 + cot² θ) + (1 + cot² θ)⁴
= 2 + 2 tan² θ – (1 + 2 tan² θ + tan² θ) – 2 – 2 cot² θ + (1 + 2 cot² θ + cot θ) =
= 2 + 2 tan² θ – 1 – 2 tan² θ – tan⁴ θ – 2 – 2 cot² θ + 1 + 2 cot⁴ θ + cot⁴ θ
= cot⁴ θ – tan⁴ θ = RHS

26. Write all the other trigonometric ratios of ∠A in terms of sec A.
Sol:

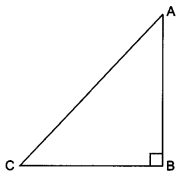
Let us consider a right-angled ∆ABC in which ∠B = 90°.
For ∠A we have

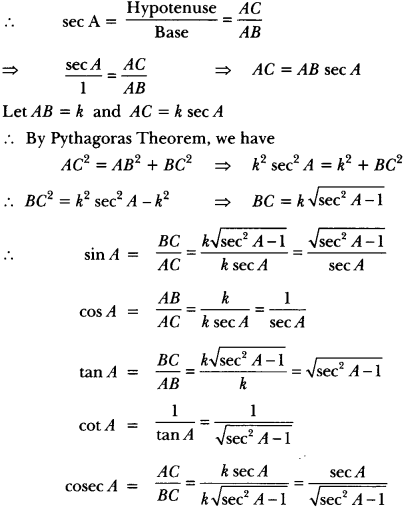
27. If cot θ = 7/8, evaluate:
(i)

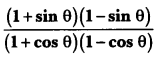
(ii) cot² θ
Sol:
Let us draw a right triangle ABC in which ∠B = 90° and ∠C = θ.