ADDITIONAL QUESTIONS AND ANSWERS:

ADDITIONAL QUESTIONS AND ANSWERS:

1. Find the angle of elevation of the sun when the shadow of a pole h m high is √3 h m long.
Ans:

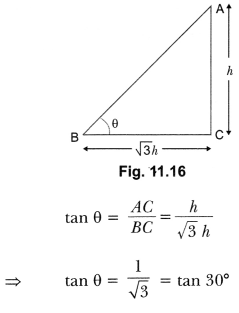
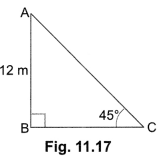
2. The height of a tower is 12 m. What is the length of its shadow when the Sun’s altitude is 45°?
Ans:

Let AB be the tower [Fig. 11.17].
Then, ∠C = 45°, AB = 12 m

∴ The length of the shadow is 12 m.

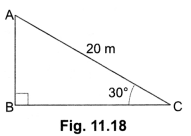
3. A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.
Ans:
Let AB be the vertical pole and AC be the long rope tied to point C.
In right ∆ABC, we have

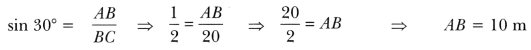
Therefore, height of the pole is 10 m.

4. The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Ans:
Let BC be the tower whose height is h metres and A be the point at a distance of 30 m from the
foot of the tower. The angle of elevation of the top of the tower from point A is given to be 30°.
Now, in right angle ∆CBA we have,

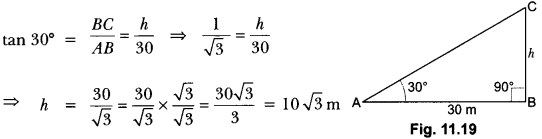
Hence, the height of the tower is 10 √3 m.

5. A tree breaks due to storm and the broken part bends, so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Ans:
In right angle ∆ABC, AC is the broken part of the tree (Fig. 11.20).
So, the total height of tree = (AB + AC)
Now in right angle ∆ABC,

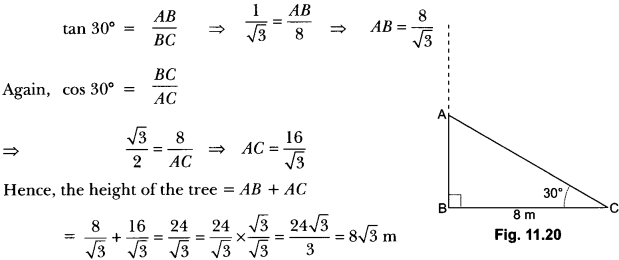
6. The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Ans:

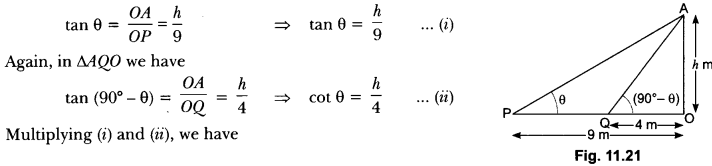
Let OA be the tower of height h metre and P, l be the two points at distance of 9 m and 4 m respectively from the base of the tower.
Now, we have OP = 9 m, OQ = 4 m,
Let ∠APO = θ, ∠AQO = (90° – θ)
and OA = h metre (Fig. 11.21)
Now, in ∆POA, we have


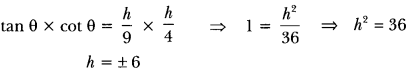
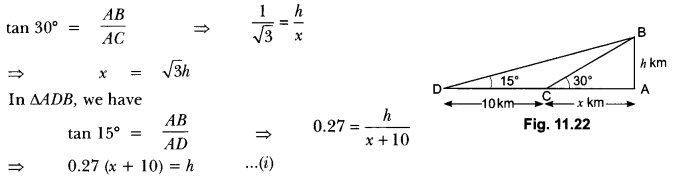
Height cannot be negative.
Hence, the height of the tower is 6 metre.

7. Determine the height of a mountain if the elevation of its top at an unknown distance from the base is 30° and at a distance 10 km further off from the mountain, along the same line, the angle of elevation is 15o°
Ans:
Let AB be the mountain of height h kilometres. Let C be a point at a distance of x km, from the base of the mountain such that the angle of elevation of the top at C is 30°. Let D be a point at a distance of 10 km from C such that angle of elevation at D is of 15°.
In MBC (Fig. 11.22), we have

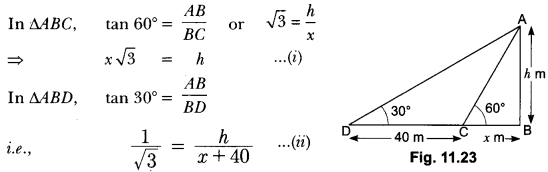
Substituting x = √3h in equation (i), we get
⇒ 0.27 ( √3h + 10) = h
= 0.27 × √3h + 0.27 × 10 = h
⇒ 2.7 = h – 0.27 × √3h
⇒ 27 = h (1 – 0.27 × √3)
⇒ 27 = h (1 – 0.46)
⇒ h = 2.70.54 = 5
Hence, the height of the mountain is 5 km.

8. The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.
Ans:
In Fig. 11.23, AB is the tower and BC is the length of the shadow when the Sun’s altitude is 60°, i.e., the angle of elevation of the top of the tower from the tip of the shadow is 60° and DB is the length of the shadow, when the angle of elevation is 30°.
Now, let AB be h m and BC be x m.
According to the question, DB is 40 m longer than BC.
So, BD = (40 + x) m
Now, we have two right triangles ABC and ABD.

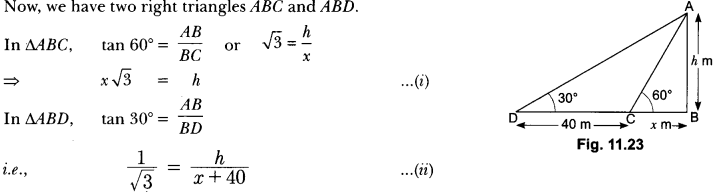
Using (i) in (ii), we get (x √3 ) √3 = x + 40, i.e., 3x = x + 40
i.e., x = 20
So, h = 20 √3 [From (i)]
Therefore, the height of the tower is 20 √3 m.

9. From a point P on the ground, the angle of elevation of the top of a 10m tall building is 30°. A flag is hosted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45o. Find the length of the flagstaff and the distance of the building from the point P. (You may take √3 = 1.732).
Ans:

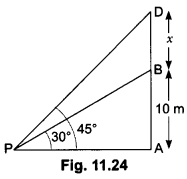
In Fig. 11.24, AB denotes the height of the building, BD the flagstaff and P the given point. Note that there are two right triangles PAB and PAD. We are required to find the length of the flagstaff, i.e., BD and the distance of the building from the point P, i.e., PA.
Since, we know the height of the building AB, we will first consider the right ∆PAB.

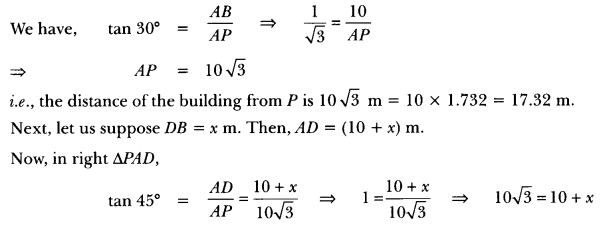
i.e., x = 100(√3 – 1) = 7.32
So, the length of the flagstaff is 7.32 m.

10. A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Ans:
Let AC be a steep slide for elder children and DE be a slide for younger children. Then AB = 3 m and DB = 1.5 m (Fig. 11.25).
Now, in right angle ∆DBE, we have

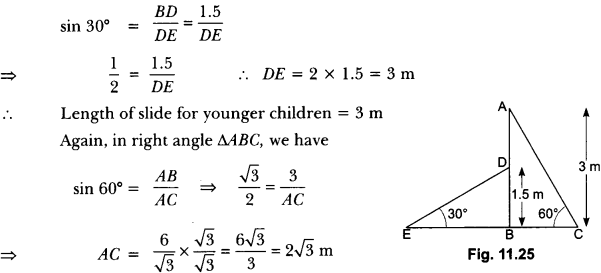
So, the length of slide for elder children is 2 √3 m.

11. A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Ans:
Let AB be the horizontal ground and K be the position of the kite and its height from the ground is 60 m and let length of string AK be x m. (Fig. 11.26)
∠KAB = 60°
Now, in right angle ∆ABK we have

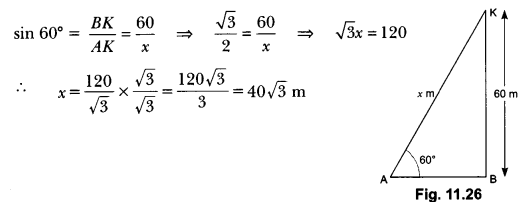
So, the length of string is 40 √3 m.

12. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Ans:
Let AB be the building and PQ be the initial position of the boy (Fig. 11.27) such that
∠APR = 30°
and AB = 30 m
Now, let the new position of the boy be P’Q’ at a distance QQ’.
Here, ∠AP’R = 60°
Now, in ∆ARP, we have

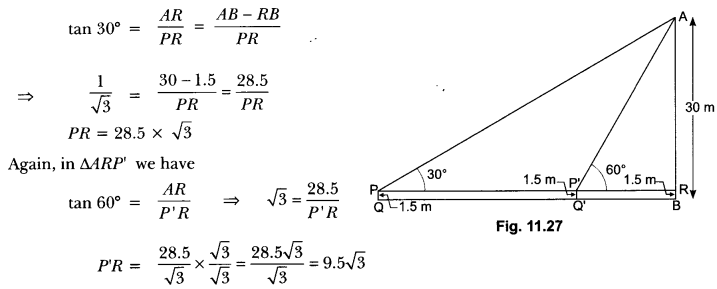
Therefore, required distance, QQ = PP’ = PR – P’R
= 28.5 √3 – 9.5 √3 = 19√3
Hence, distance walked by the boy is 19√3 m.

13. From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.
Ans:
In Fig. 11.28, A and B represent points on the bank on opposite sides of the river, so that AB is the width of the river. P is a point on the bridge at a height of 3 m, i.e., DP = 3m. We are interested to determine the width of the river, which is the length of the side AB of the ∆APB.
In right ∆ADP, ∠A = 30°

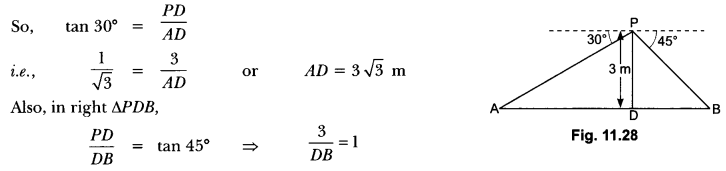
∴ DB = 3m
Now, AB = BD + AD = 3 + 3 √3 = 3 (1 + √3) m
Therefore, the width of the river is 3(√3 + 1) m.

14. As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Ans:

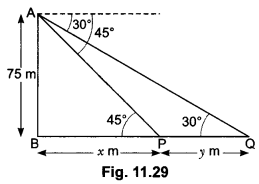
Let AB be the lighthouse of height 75 m and P, Q be the position of the two ships whose angles of depression are 45° and 30°, respectively (Fig. 11.29). Let BP = x m and PQ = y m, we have
∠APB = 45° and ∠AQB = 30°
Now, in ∆ABP we have
tan 45° = ABBP
⇒ 1 = 70x
⇒ x = 75 m …..(i)
Again, in ∆ABQ we have
tan 30° = ABBQ
⇒ 13√ = 75x+y
⇒ x + y = 75 √3 ……(ii)
From (i) and (ii), we have
75 + y = 75 √3
y = 75 √3 – 75
⇒ y = 75(√3 – 1)
Hence, the distance between two ships is 75(√3 – 1) metres.

15. Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. (Use √3 = 1.73]
Ans:
Let the distance between the two ships be d.
Let the distance of one ship from the light house be x metres. Then, the distance of the other ship from the light house will be (d – x) metres.

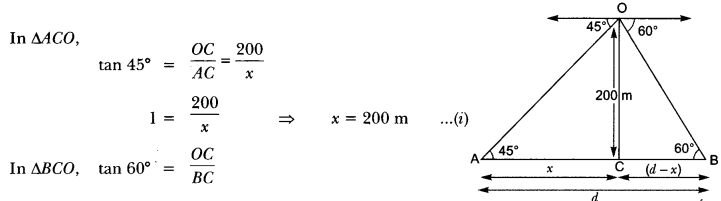
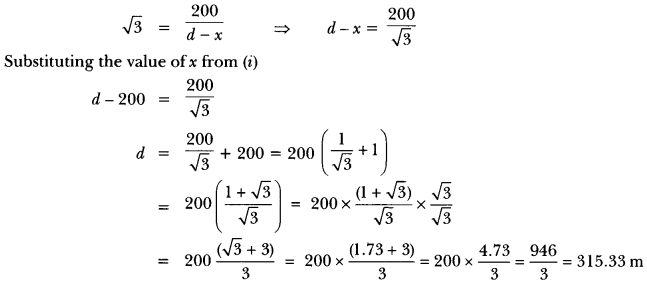
16. Two men on either side of a 75 m high building and in line with base of building observe the angle of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use √3 = 1.73)
Ans:

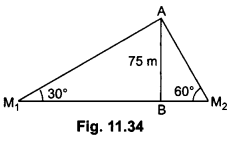
(i) In ∆ABM₁
ABBM1 = tan 30° = 13√
⇒ BM₁ = 75 √3 m

(ii) In ∆ABM₂
ABBM2 = tan 60° = √3
⇒ BM2 = 753√ = 25 √3 m
∴ M₁ M₂ = M₁B + BM₂
= 75√3 + 25 √3 = 100 √3 m = 173 m
∴ Distance between the two men = 173 m.

17. A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
Ans:

Let the speed of boat be x m/min
∴ CD = 2x
In ∆ABC
150y = tan 60°
⇒ y =1503√ = 50√3 m
In ∆ABD
150y+2x = tan 45°
⇒ 150 = 50√3 + 2x
⇒ x = 25(3 – √3)
Speed = 25(3 – √3 ) m/min
∴ = 25 × 60 (3 – √3) m/h
= 1500 (3 – √3) m/h

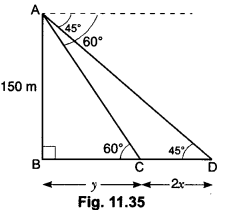
18. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60°, respectively. Find the height of the tower.
Ans:
Let AB be a building of height 20 m and BC be the transmission tower of height x m and D be any point on the ground (Fig. 11.36).
Here, ∠BDA = 45° and ∠ADC = 60°
Now, in ∆ADC, we have

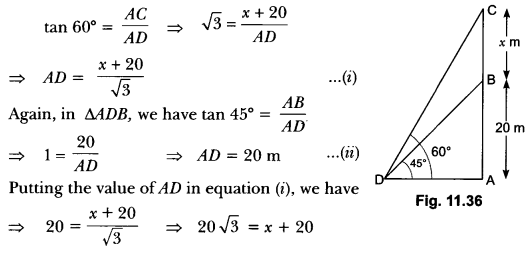
⇒ x = 20√3 – 20 = 20 (√3 – 1)
= 20 (1.732 – 1) = 20 × 0.732 = 14.64 m
Hence, the height of tower is 14.64 m.

19. Find the angle of elevation of the sun when the shadow of a pole h m high is √3 h m long.
Ans:

In ∆ABC

θ = 30°

20. From the top of a 60 m high building, the angles of depression of the top and the bottom of a tower are 45° and 60° respectively. Find the height of the tower. [Take √3 = 1.73]
Ans:
Let the height of the building be AE = 60 m, the height of the tower is ‘h’. The distance between the base of the building and the tower be ‘d’.
In ∆ADE,

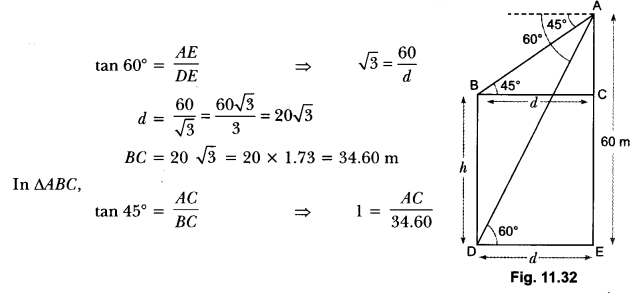
⇒ AC = 34.60 m
Now, height of tower = AE – AC = 60 – 34.60 = 25.4 m

21. Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. (Use √3 = 1.732]
Ans:
Let AD be the light house and its height be h. The distance of one ship from the light house is x and that of other ship is 100 – x.
In ∆ADB,

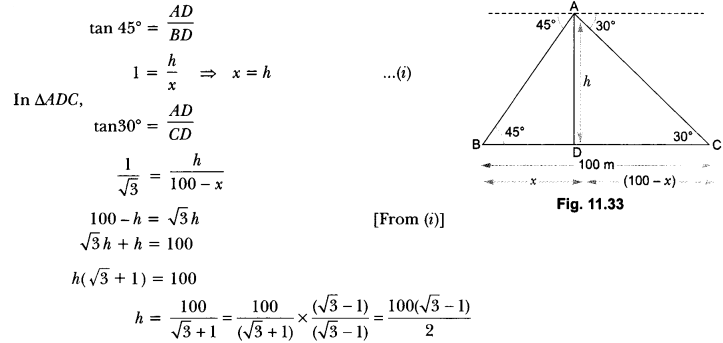
= 50 × (1.732 – 1)
h = 36.6 m