SAMPLE PAPER GOA BOARD : MARCH 2013
1(A) Select and write the most appropriate alternative from those provided in the bracket :
The probability of an event that is sure to happen is ____.
[ − 1 , 0 , 1 , greater than 1 ]
Ans : 1
(B) A bag contains 10 red marbles, 16 green marbles, and 14 white marbles. One marble is drawn at random from the bag. Find the probability of getting :
1.A red marble
Ans : Favourable outcomes = 10 red marbles
Possible outcomes = 10 + 16 + 14 = 20
Probability of getting a red marble
= \frac{10}{40}
= \frac{1}{4}
2.Anon red marble
Ans : Favourable outcomes = 16 + 14
= 30 non red marbles
Possible outcomes = 40
Probability of getting a non red marble
= \frac{30}{40}
= \frac{3}{4}
(C) Attempt ANY ONE of the following. Find roots of the quadratic equation :
1. 4x2 − 4x −15 = 0
(By factorization Method)
Ans : 4x2 − 4x − 15 = 0
4x2 − 10x + 6x − 15 = 0
2x (2x − 5) + 3 (2x − 5) = 0
(2x − 5) (2x +3) = 0
Either 2x −5 = 0 or 2x + 3 = 0
x = \frac{5}{2} OR x = − \frac{3}{2}
2. 2x2− 5x − 3 = 0
(By Quadratic Formula Method)
Ans : 2x2− 5x − 3 = 0
Here a = 2 , b = − 5 and c = − 3
D = b2− 4ac
= ( − 5)2− 4 × 2 ( − 3)
= 25 + 24
= 49
Roots are given as ( \frac{− b ±\sqrt{D} }{2a} )
= \frac{− (− 5) ±\sqrt{49} }{2 × 2}
= 5 ± \frac{7}{4}
Either 5 + \frac{7}{4} OR 5 − \frac{7}{4}
\frac{12}{4} OR − \frac{2}{4}
The roots are 3 OR − \frac{1}{2}
(D) The area of an exhibition hall is 96 sq. m. If the length and breadth be increased by 1 m each, the area increases by 21 sq. m. Find the length and breadth of the hall.
Ans : The area of the rectangular hall is 96 sq. cm.
If the length is x meters, then breadth is \frac{96}{x} meters.
If the length is made (x + 1)m and breadth is made ( \frac{96}{x} + 1) m then new area is
96 + 21 = 117 sq. m
(x + 1) [ \frac{96}{(x + 1)} ] = 117
96+ x +\frac{96}{(x + 1)} = 117
96x + x2 + 96 + x = 117 x
x2 − 20x + 96 = 0
x2 − 12x − 8x + 96 = 0
x (x − 12) − 8 (x − 12) = 0
(x − 8) (x − 12) = 0
Either x − 8 = 0 OR x − 12 = 0
Either x = 8 OR x = 12
As length is bigger than breadth,
The length is 12 m and breadth is 8 m.
2(A) Select and write the most appropriate alternative from those provided from brackets :
The solution of the equation x + 2y = 4 and 2x −3y = 1 is ___.
[ (x = 1 , y= 2) : (x = 2 , y= 1) : (x = − 1, y = − 2) : (x = 2, y = 1 )
Ans : (x = 2, y = 1)
(B) The following is a pair of linear equations in two variables :
x + ky − 2 = 0
2x+ 5y − 3 =
Answer the following questions with reference to the given pair of equations :
1. Write down the conditions for no solution.
Ans : \frac{1}{2} = \frac{k}{− 5} ≠ \frac{− 2}{− 3}
2. Find the value of k.
Ans : \frac{1}{2} = \frac{k}{− 5}
k = \frac{− 5}{2}
(C) Find the solutions of ANY ONE of the following pairs of linear equations by the method specified in the bracket :
1. 4x + 3y = 17 and 5x − 2y = 4
(By eliminating method)
Ans : 4x + 3y = 17 … (1)
5x − 2y = 4 … (2)
Multiply Eq. (1) by 2, we get 8x + 6y = 34
Multiply Eq. (2) by 3, we get 15x − 6y = 12
____________
Adding 23x = 46
x = \frac{46}{23} = 2
Substituting x = 2 in eq (1),
We get 4 × 2 + 3y = 17
3y = 17 − 8
3y = 9
y = \frac{9}{3} = 3
The solution is x = 2 , y = 3.
2. 6x+ 5y = 8 and 9x − 2y = 31
(By substitution method)
Ans : 6x + 5y = 8 … (1)
9x − 2y = 31
9x – 31 = 2y
y = 9x − \frac{31}{2} … (2)
Substituting the value of y in Eq (1)
6x + 5 (9x – \frac{31}{2} ) = 8
12x + 5 (9x – 31) = 16
12x + 45x − 155 − 16 = 0
57x − 171 = 0
x = \frac{171}{57}
= 3
Substituting x = 3 in Eq (1)
6 × 3 + 5y = 8
5y = 8 − 18
y = − \frac{10}{5}
= − 2
The solution is x = 3, y = − 2
(D) Notebooks were equally distributed to the students in std 6th. If there were 20 students more each would have received 2 books less and if there were 20 students less each would have received 3 books more. Find the number of students in the class and the number of books received by each student.
Ans : Let the number of students in the class be x
And the number of notebooks received by each student be y.
Total number of notebooks distributed is xy,
By the given condition, the two-equation are,
( x + 20) ( y − 2) = xy … (1)
(x − 20) ( y + 3) = xy … (2)
Eq. (1) xy − 2x + 20y − 40 = xy
− 2x + 20y = 40
x − 10y = − 20 .. (3)
Eq. (2) xy + 3x − 20y − 60 = xy
3x − 20y = 60 … (4)
3 × eq (3) gives 3x − 30y = − 60 … (5)
− + +
______________
10y = 120
y = \frac{120}{10}
= 12
Substituting y = 12 in Eq (3),
x − 10 × 12 = − 20
x = − 20 + 0
x = 100
No. of students is 100 and each student received 12 notebooks.
3(A) Select and write the most appropriate alternative from those provided in the brackets :
The product of two numbers is 168 and their H.C.F is 7 then their L.C.M is ____.
[ 14 , 24 , 46 , 1 176 )
Ans : 24
(B) Divide the polynomial x3 − 5x2 + 3x − 3 by x2 −2 , and find the quotient and the remainder.
Ans :
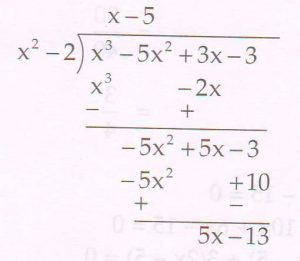
Quotient = x − 5
Remainder = 5x − 13
(C) If two zeros of the polynomial x4 −13x3 −33x2 + 39x + 90 are \sqrt{3} and − \sqrt{3} find the other zeros of the polynomial.
Ans : Since \sqrt{3} and − \sqrt{3} are the two zeros,
(x − \sqrt{3} ) (x + \sqrt{3} ) = x2 −3 is a factor of the polynomial
Let us divide the given polynomial by x2 −3
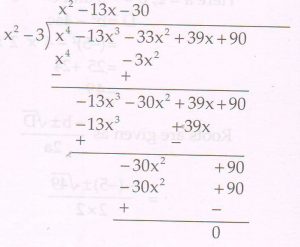
Factorising x2 − 13x − 30 we get
= (x + 2) (x − 15)
The other zeros are given by x + 2 = 0 and x − 15 = 0
x = − 2 and x = 5
The required other two zeros are − 2 and 15.
(D) Prove that \sqrt{5} is an irrational number.
Proof: Let us assume, to the contrary, that \sqrt{5} is rational.
We can find integers a and b () such that = a/b where a and b are coprime
b \sqrt{5} = a
5b2 = a2 … (1)
a2 is divisible by 5
a is divisible by 5 … (2)
a = 5c, for some integer c …. (3)
Substitute (3) in (1), we get
5b2 = 25c2
b2 = 5c2
b2 = 3c2
b2 is divisible by 5.
b is divisible by 5 … (3)
From (2) and (4), a and b are both divisible by 5.
This contradicts our assumption that a and b are coprime.
\sqrt{5} is rational is a wrong assumption.
\sqrt{5} must be irrational.
4(A) Select and write the most appropriate alternative from those provided in the bracket :
The 4th term of an A.P whose first term is 21 and the common difference is − 3 is ____.
[ 12 , 33 , 9 , − 9 )
Ans : 12
(B) The following table gives the literacy rate (in percentage) of 35 cities :
|
Literacy rate (in %) |
Number of cities |
|
45 − 55 |
5 |
|
55 − 65 |
8 |
|
65 − 75 |
13 |
|
75 − 85 |
6 |
|
85 − 95 |
3 |
Find the mode of this data.
Ans : The maximum class frequency is 13.
The modal class is 65 − 75
Where l = lower limit of the modal class = 65
h = class size = 10
f1 = frequency of the modal class = 13
f0= frequency of the class preceding the modal class = 8
f2 = frequency of the class succeeding the modal class = 6
Mode = l + \frac{ f_{1}- f_{0} }{2 f_{1} - f_{0} - f_{2} } × h
= 65 + ( \frac{13 - 8 }{2 × 13 - 8 - 6} ) × 10
= 65 + \frac{5}{12} × 10
= 65 + \frac{25}{6}
= 65 + 4.167
= 69.167
Mode of this data is 69.167
(C) The second and seventh terms of an Arithmetic progression are 2 and 22 respectively. Find the sum of the first 30 terms.
Ans : The nth term is given by, an = a + (n − 1) d
a + ( 2 − 1) d = 2 … (1)
and a + (7 − 1) d = 22 …. (2)
From (1) a + d = 2
From (2) a + 6d = 22
Subtracting (2) from (1) we get
− 5d = − 20
d = 4
From (1) a + (2 − 1) 4 = 2
a = 2 − 4
a = − 2
Sum of n terms, Sn = \frac{n}{2} [ 2 a + (n − 1 ) d ]
S30 = \frac{30}{2} [ 2 × ( − 2) + (30 − 1) × 4
= 15 ( − 4 + 116 )
= 15 × 112
= 1680
Sum of first 30 terms is 1680.
(D) The table below shows the number of wickets taken by a group of 35 bowlers in a one-day cricket match.
Taking the class-mark (denoted by ‘a’) of the class interval 35 − 45 as the ‘assumed mean’, rewrite and complete the table, and also find the mean of the data.
Ans :
|
C. I. |
fi |
xi |
Di= xi−40 |
fidi |
|
15 − 25 |
5 |
20 |
− 20 |
− 100 |
|
25 − 35 |
6 |
30 |
− 10 |
− 60 |
|
35 − 45 |
10 |
40 |
0 |
0 |
|
45 − 55 |
6 |
50 |
10 |
60 |
|
55 − 65 |
5 |
60 |
20 |
100 |
|
65 − 75 |
3 |
70 |
30 |
90 |
|
Total |
∑fi = 35 |
|
|
∑fidi= 90 |
Assumed mean, a = 40
Mean, x = a + \frac{∑fidi }{∑fi }
= 40 + \frac{90}{35}
= 40 + \frac{18}{7}
= 40 + 2.57
= 42.57
5(A) Select and write the most appropriate alternative from those provided in the brackets :
ΔDEF ∼ ΔXYZ and if
\frac{ar (Δ DEF)}{ar (Δ XYZ)} = \frac{25}{64} then \frac{EF}{YZ} = ____.
[ \frac{25}{64} , \frac{8}{5} , \frac{ \sqrt{5} }{ \sqrt{8} } , \frac{5}{8} ]
Ans : \frac{5}{8}
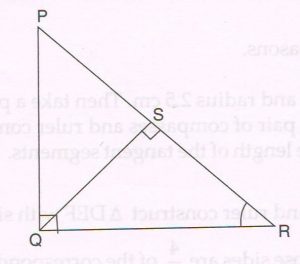
(B) With reference to the given figure and the given conditions write only the proof with reasons of the following theorem.
Given: In ΔPQR, ∠PQR = 90° QS _|_ PR, where S lies on PR.
Prove that: PR2 = PQ² + QR2
Proof :
In ΔPSQ and ΔPQR
∠P = ∠P (common side)
∠PSQ = ∠PQR (each is a right angle)
ΔPSQ ∼ ΔPQR (AA similarity criterion)
= \frac{ PQ}{RS} = \frac{PS}{PQ}
PQ2 = PS × PR … (1)
Similarly we can prove that ΔQSR ∼ ΔPQR
= \frac{ QR}{PR} = \frac{SR}{PR}
QR2 = SR × PR … (2)
Adding (1) and (2)
PQ2 + QR2 = PS × PR × SR × PR
= PR (PS + SR)
= PR PR
= PR2
PR2 = PQ2 + QR2
(C) The perpendicular from K to side MN of ΔKMN intersects MN at R such that 3MR = RN.
Prove that: 2KN2 = 2KM2 + MN2
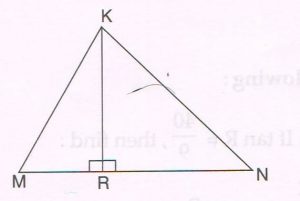
Proof :
MN = MR + RN
= MR +3MR (using given condition)
= 4MR
MR = \frac{1}{4} MN and RN = \frac{3}{4} MR … (1)
Now in right ΔKRN, by Pythagoras theorem,
KN2 = KR2 RN2
= (KM2 – MR2) + RN2 (using right DKRM)
= KM2 − \frac{1}{16} MN2 + \frac{9}{16} MN2 [using (1)]
= KM2 + \frac{8}{16} MN2
KN2 = KM2 + \frac{1}{2} MN2
Multiplying by 2, we get
2KN2 = 2KM2 + MN2
(D) As observed from the top of a 75 m high lighthouse from the sea level, the angles of depression of two ships are 30° and 60°. If one ship is exactly behind the other on the same side of the lighthouse find the distance between the ships.
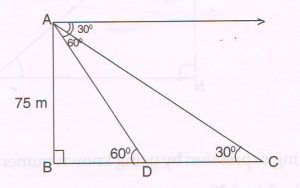
Ans : Let BD = x and BC = y
DC = y − x …(1)
In right ΔABD, tan 60° = \frac{AB}{BD}
\sqrt{3} = \frac{75}{x}
x = \frac{75}{ \sqrt{3} } … (2)
In right Δ ABC, tan 30° = \frac{AB}{BC}
\frac{1}{ \sqrt{3} } = \frac{75}{y}
y = \frac{75}{ \sqrt{3} } … (3)
From (1) (2) and (3)
DC = y − x = \frac{75}{ \sqrt{3} } / \sqrt{3}
= 75 ( \frac{ \sqrt{3} - 1 } { \sqrt{3} } )
= 75 ( \frac{ 3 - 1 } { \sqrt{3} } )
= \frac{150}{ \sqrt{3} } × \frac{ \sqrt{3} }{ \sqrt{3} }
= \frac{150 } { \sqrt{3} }
= 50 \sqrt{3}
Distance between the two ships is 50 meters.
6(A) Select and write the most appropriate alternative from those provided in the bracket :
If PA and PB are two tangent segments to a circle with centre O such that ∠APB = 62° then ∠AOB = _____.
[ 62° , 31° , 180° , 118° ]
Ans : 118°
(B) In the figure below ‘G’ is a point in the exterior of the circle with centre O. And GH and GF are two tangents to the circle at H and F respectively.
Prove that: GH = GF
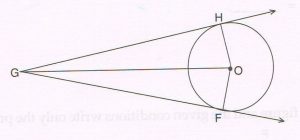
(Write only the proof with reasons).
Proof : Since GH and GF are tangents to the circle at H and F,
They are perpendicular to the radii OH and OF respectively.
ΔGHO and ΔGFO are right triangles, where
OH = OF (radii of the same circle)
OG = OG (common hypotenuse)
ΔGHO ≅ ΔGFO (RHS congruency)
GH = GF (cpct)
(C) Draw a circle with centre O and radius 2.5 cm. Then take a point R at a distance of 6.7 cm from the centre of the circle. Using a pair of compass and ruler construct two tangents RB and RC to the circle. Measure and state the length of the tangent segments.
Ans :
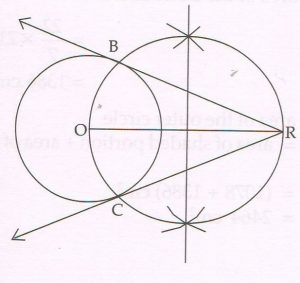
Length of each tangent segment is 6.2 cm.
(D) Using a pair of compass and ruler construct ΔDEF with side EF = 4.5 cm, DE = 5cm, ∠E = 60°. Then construct ΔD’EF’ whose sides are \frac{4}{5} of the corresponding sides of ΔDEF.
Ans :
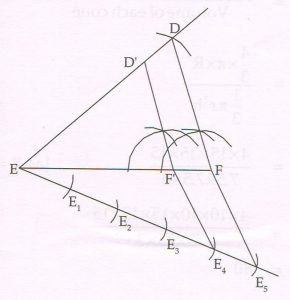
7(A) Select and write the most appropriate alternative from those provided in the bracket :
The numerical value of the trigonometric ratio tan 30° = ____.
[ \sqrt{3} , 1 , \frac{1}{ \sqrt{3} } , not defined )
Ans : \frac{1}{ \sqrt{3} }
(B) Attempt ANY ONE of the following :
1. In ΔPNR, ∠N = 90°. If tan R = \frac{40}{9} , then find:
(a) the length of PR
(b) the value of sin P
(c) the value of cot R.
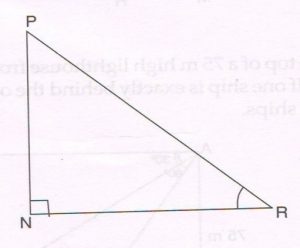
Ans : tan R = \frac{40}{9}
(a) By Pythagoras theorem
PR2 = PN2 + NR2
=402 + 92
= 1600 + 81
= 1681
PR = \sqrt{1681}
=41
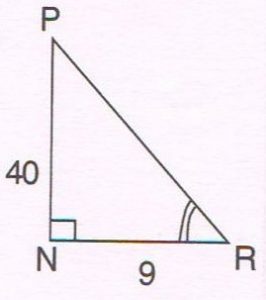
(b) sin P = \frac{opp \thinspace \thinspace side \thinspace \thinspace to \thinspace \thinspace ∠P }{hypotenuse}
= \frac{9 }{41}
(c) cot R = \frac{adj \thinspace \thinspace side \thinspace \thinspace \thinspace to \thinspace \thinspace ∠R }{opp \thinspace \thinspace side \thinspace \thinspace to \thinspace \thinspace ∠R}
= \frac{9 }{40}
2. Evaluate the following expression by using known numerical values of trigonometrical ratios.
5 cos2 60 + 4 sec2 30 − 3 tan2 30
Ans : 5 cos2 60 + 4 sec2 30 − 3 tan2 30
= 5 × \big( \frac{1}{2} \big)² + 4 × \big( \frac{2}{ \sqrt{3} } \big)² − 3 × \big( \frac{1}{ \sqrt{3} } \big)²
= \frac{5}{4} + \frac{16}{3} − 1
= 15 + 64 − \frac{12}{12}
= \frac{67}{12}
= 5 \frac{7}{12}
(C) With the help of a suitable figure prove that
Sin2 B + cos2 B =1
Ans :
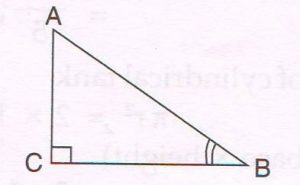
In right Δ ABC, ∠C = 90°.
By Pythagoras theorem
AC2 + BC2 = AB2
Dividing by AB2,
\frac{AC²}{AB²} + \frac{BC²}{AB²} = \frac{AB²}{AB²}
\big( \frac{AC}{AB} \big)² + \big( \frac{BC}{AB} \big)² = 1
But \frac{AC}{AB} = sin B and \frac{BC}{AB} = cos B
( sin B)² + ( cos B)² = 1
sin² B + cos² B = 1
(D) Attempt each of the following :
1. Find the distance between the points A ( 2, − 3) and B ( 5, 6).
Ans : By distance formula,
AB = \sqrt{( 2 − 5)² + ( − 3 − 6)²}
= \sqrt{9 + 81}
= \sqrt{90}
= 3 \sqrt{10}
2. Find the value of k if the points A( 2, 3) , B ( 4, k) C ( 6, 3) are collinear.
Ans : Since the points are collinear, then the area of ΔABC = 0
\frac{1}{2} [ (2 (k – 3) + 4 ( 3 − 3 ) + 6 (3 − k) ] = 0
2k − 6 + 18 − 6k = 0
− 4k + 12 = 0
− 4k = − 12
k = 3
8 (A) Select and write the most appropriate alternative from those provided in the bracket :
1. In a circle of radius 21 cm, an arc of length 22 cm subtends an angle at the centre. If π = \frac{27}{7} , then ∅ = ___°.
[ 30 , 60 , 90 , 120 )
Ans : 60
2. Two cubes each of side 3 cm are joined end to end. The surface area of the resulting cuboid is ______cm2.
[ 18 , 27 , 45 , 90)
Ans : 90
(B) Attempt each of the following :
1. A sector of 36° is cut out from a circle of radius 6 cm. find the area of the circle without substituting the value of π.
Ans : Area of sector O − PXB = \frac{∅}{360} × π r2
= \frac{36}{360} × π × 62
= \frac{1}{10} × π × 36
= 18 \frac{π}{5} cm2
2. The area of the base of a cylindrical tank is 2 cm2 and the height is 1.5 m. find the capacity of the cylindrical tank without substituting the value of π.
Ans : Volume of cylindrical tank
π r2 = 2 × 1.5
(Area of base height) = 3 m³
The capacity of the tank is 3 m³
(C) In the following figure two concentric circles are shown. The radius of the inner circle is 21 cm and the area of the shaded region is 1078 sq.cm, then find:
(take π = \frac{22}{7} )
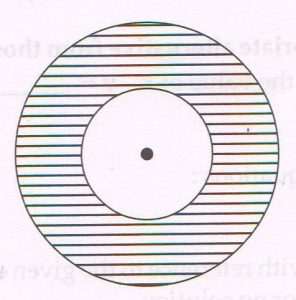
1. Area of inner circle.
Ans :Area of the inner circle = π r2
= \frac{22}{7} × 21 × 21
= 1386 cm2
2. Area of outer circle.
Ans : Area of the outer circle
= area of shaded portion + area of the inner circle
= (1078 + 1386) cm2
= 2464 cm2
(D) A solid metallic sphere of diameter 30 cm is melted and recast into smaller cones each of radius 7.5 cm and perpendicular height 3 cm. find the number of cones formed.
Ans : Number of cones formed
= \frac{Volume of the solid sphere}{ Volume of each cone}
= \frac{4}{3} × π × R³ / \frac{1}{3} π r²h
=\frac{4 × 15 × 15 × 15 × 15 }{7.5 × 7.5 × 3 }
(as R = \frac{30}{2} cm)
= \frac{4 × 10 × 10 × 15 × 15 × 15}{75 × 75 × 3}
= 80