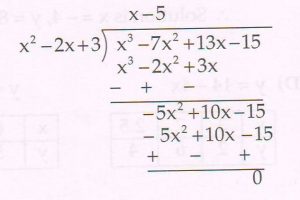SAMPLE PAPER GOA BOARD MARCH 2014
1(A) Select and write the most appropriate alternative from those provided in the bracket :
The H.C.F. and L.C.M. of two numbers is 2 and 208 respectively. If one of the numbers is 16 then the other number is _____.
[ 8 , 26 , 32 , 104 ]
Ans : 26
( B) Attempt the following :
1. Find the product of the zeros of the quadratic polynomial 3x2 − 7x + 15.
Ans : Product of the zeros,
(a = 3 , b = − 7, c = 15)
b = \frac{c}{a} = \frac{15}{3} = 0
2. Find the zeros of the quadratic polynomial (x2 −5).
Ans : To find the zeros, let x2 −5 = 0
x2 = 5
x = ± \sqrt{5}
The zeros are \sqrt{5} and − \sqrt{5}
( C) On dividing the polynomial (x3− 7x2 + 12x +16) by a polynomial g(x), the quotient and the remainder are ( x2 −2x + 3) and (31 − x ) respectively. Find g(x).
Ans : By division algorithm, p(x) = g(x) x q(x) + r(x)
x3− x2 + 12x + 16 = g(x) x ( x2 – 2x + 3) + ( 31 − x)
( x2 − 2 +3) g (x) = x3 − 7x2 + 12x + 16 − 31 + x
= x3 − 7x2 + 13x − 15
g(x) =( x3 −7x2 + 13x − 15) ÷ (x2 −2x + 3)
g(x) = x − 5
(D) Assuming that √3 is an irrational number, prove that 7 − 2 \sqrt{3} is also an irrational number.
Ans : Let us assume, to the contrary, that 7 − 2 \sqrt{3} is a rational number.
That is, we can find coprime a and b ( b ≠ 0) such that
7 − 2 = \frac{a}{b}
2 = 7 − \frac{a}{b}
\sqrt{3} = 7b − \frac{a}{2b}
Since a and b are integers 7b − \frac{a}{2b} is also an integer and is rational
This means \sqrt{3} is rational
But this contradicts the fact that \sqrt{3} is irrational.
Our assumption that 7 − 2 \sqrt{3} is rational, must be wrong.
7 − 2 \sqrt{3} is irrational
2 (A) Select and write the most appropriate alternative from those provided in the bracket :
A card is drawn from a well shuffled deck of 52 cards. Therefore the probability of getting a king of black colour is ____.
[ \frac{1}{4} , \frac{1}{13} , \frac{1}{26} , \frac{25}{26} ]
Ans : \frac{1}{26}
( B) A die is thrown once. What is the probability that the number appearing on the top of the die is :
1. An even number
Ans : Probability of getting an even number on the top
= \frac{Number \thinspace \thinspace of \thinspace \thinspace favourable \thinspace \thinspace outcomes}{Number \thinspace \thinspace of \thinspace \thinspace all \thinspace \thinspace possible \thinspace \thinspace outcomes}
= \frac{3}{6} = \frac{1}{2}
2 . Less than 5
Ans : Probability of getting less than 5 on the top
= \frac{Number \thinspace \thinspace of \thinspace \thinspace favourable \thinspace \thinspace outcomes}{Number \thinspace \thinspace of \thinspace \thinspace all \thinspace \thinspace possible \thinspace \thinspace outcomes}
= \frac{4}{6} = \frac{2}{3}
( C) Find the roots of ANY ONE of the following :
1. 6x2− 13x − 5 = 0
( By factorization method)
Ans : 6x2− 13x − 5 = 0
6x2− 15x + 2x − 5 = 0
3x ( 2x − 5 ) + 1 ( 2x − 5 ) = 0
( 2x − 5 ) ( 3x + 1) = 0
Either 2x − 5 = 0 OR 3x + 1 = 0
x = \frac{5}{2} OR x = − \frac{1}{3}
2. 3x2 − 14x − 5 = 0
( By using the quadratic formula )
Ans : 3x2 − 14x − 5 = 0
Here, a = 3, b = − 14, c = − 5
D = b2 − 4ac
= − (14)2 − 4 × 3 × ( − 5)
= 196 + 60
= 256
By quadratic formula, roots are given by
x = − b ± \frac{ \sqrt{D} }{2 b}
= − ( − 14 ) ± \frac{ \sqrt{256} }{2 × 3}
= 14 ± \frac{16}{6}
Either x = 14 + \frac{16}{6} OR x = 14 − \frac{16}{6}
Either x = \frac{30}{6} OR x = − \frac{1}{3}
x = 5 or x = − \frac{1}{3}
( D) The sum of the present ages of the father and his son is 45 years. Five years ago, the product of their ages was 34 years. Find their present ages.
Ans : Let the father’s age be x years
The son’s age is ( 45 − x ) years
Five years ago, their ages were (x − 5 ) years and (45 − x − 5) years respectively.
From the given condition,
(x − 5 )( 40 − x ) = 34
40 x − x2 − 200 + 5x − 34 = 0
− 2 + 45x − 234 = 0
x2 − 45x + 234 = 0
x2 − 39x − 6x + 234 = 0
x (x − 39 ) ( x − 39 ) = 0
( x − 39 ) ( x − 6 ) = 0
Either x − 39 = 0 or x − 6 = 0
x = 39 or x = 6
Father’s age is 39 years and son’s age is 6 years.
3 ( A) Select and write the most appropriate alternative from those provided in the bracket :
The solution of the equation 2x + 3y = 2 and x + y = 2 is _____.
[ (x = 2 , y =4 ) , (x = 4, y = − 2 ) , (x = -2, y = − 2 ) , (x = 4, y = 2) ]
Ans : x = 4 , y = − 2
(B) The following is a pair of linear equations in two variables.
3x + ky −10 = 0
2x − 8y − 7 = 0
Answer the following questions with reference to the given pair of equations.
(i). Write down the conditions for no solution.
Ans : Condition for no solution.
= \frac{a1}{a2} = \frac{b1}{b2} ≠ \frac{c1}{c2}
Here a1 = 3 a2 = 2 b1 = k b2 = − 8 c1 = − 10 c2 = − 7
\frac{3}{2} = \frac{k}{− 8} ≠ \frac{− 10}{− 7} ,
condition for no solution
(ii). Find the value of k.
Ans : \frac{3}{2} = \frac{k}{ − 8}
2k = − 24
k = − \frac{24}{2}
k= − 12
( C) Find the solution of ANY ONE of the following :
1. 2x − 3y = 12
4x − 5y = 22
( By elimination method )
Ans : 2x − 3y = 12 … (1)
4x − 5y = 22 … (2)
Eq. (1) × 2, 4x − 6y = 24 … (3)
− + −
______________
Subtracting y = − 2
Substituting y = − 2 in eq (1),
We get 2x − 3 ( − 2) = 12
2x + 6 = 12
2x = 6
x = 3
Solution is x = 3 , y = − 2
2. 2x + 3y = 16
4x + 5y = 24
( By cross multiplication method)
Ans : 2x + 3y − 16 = 0
4x + 5y − 24 = 0
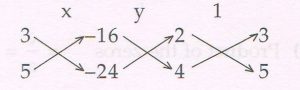
= \frac{x}{3 (−24) − 5(− 16)}
= \frac{y}{(− 16) ×4 − 2(− 24)}
= \frac{1}{2 ×5 −4 × 3}
\frac{x}{− 72 + 80}
= \frac{y}{ − 64 + 48}
= \frac{1}{10 − 12} \frac{x}{8}
=\frac{y}{ − 16}
= \frac{1}{ − 2}
x = \frac{8}{− 2} = − 4
y = \frac{ − 16}{− 2} = 8
Solution is x = − 4 , y = 8
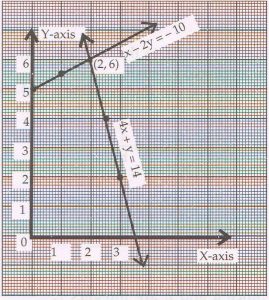
(D) Find the solution of the following pair of linear equations graphically.
4x + y = 14 and x − 2y = − 10
Rewrite and complete the following tables:
4x + y = 14
|
x |
|
|
|
|
y |
|
|
|
x − 2y = − 10
|
x |
|
|
|
|
y |
|
|
|
( Plot at least 3 points for each line on a graph paper.)
Ans : y = 14 − 4x
|
x |
3 |
2 |
2.5 |
|
y |
2 |
6 |
4 |
y = x + 10 /2
|
x |
0 |
2 |
1 |
|
y |
5 |
6 |
5.5 |
4( A) Select and write the most appropriate alternative from those provided in the brackets :
The common difference of arithmetic progression − 1 ,− 6 , − 11… is ____.
[ − 17 , − 7 , − 6 , − 5 ]
Ans : − 5
(B) The following tables shows the distribution of marks of 62 students in a Mathematics test. Find the mode of the data given below.
Ans : Here the maximum class frequency is 18
The modal class is 30 − 45
Lower limit, l = 30, class size, h = 15
Frequency of the modal class, f1 = 18
Frequency of the class preceding the modal class, f0 = 14
Frequency of the class succeeding the modal class, f2 = 10
Mode = l + ( \frac{ f_{1} - f_{0} }{2 f_{1}- f_{0} - f_{2} } ) h
= 30 + ( \frac{18 - 14}{2 × 18 - 14 - 10} ) × 15
= 30 + ( \frac{4}{36 - 24} ) × 15
= 30 + \frac{4}{12} × 15
= 35
( C) If the 5th and 12th terms of an A.P. are 30 and 65 respectively, what is the sum of the first 20 terms of the A.P. ?
Ans : nth term = a + ( n − 1 ) d
a = a + ( 5 − 1 ) d = 30
a12 = a + ( 12 − 1 ) d = 65
a + 4d = 30 … (1)
And a + 11d = 65 … (2)
− − −
___________
− 7 d = − 35
d = 5
From (1) a + 4 × 5 = 30
a = 10
Sum of the first 20 terms = S20
= \frac{n}{1} [ 2a + (n − 1 ) d ]
=\frac{20}{2} [ 2 × 10 + ( 20 − 1) 5 ]
= 10 ( 20 + 19 × 5 )
= 10 ( 20 + 95)
= 10 × 115
= 1150
( D)The following table shows the marks scored by 60 students in a test.
Taking the class- mark denoted by ‘a’ of interval 60 −80 as the assumed mean, rewrite and complete the table, and also find the mean of the marks obtained.
Ans :
Mean
, x
= a + \frac{∑fidi}{∑fi}
= 70 + \frac{ −780}{60}
= 70 − 13
= 57
5 (A) Select and write the most appropriate alternative from those provided in the bracket :
QA and QB are tangent segments from external point Q to a circle with centre O at A and B respectively. If ∠AOB = 130° then, ∠AQB = ____.
[ 25° , 50°, 90° , 260° ]
Ans : 50°
( B) Given : Point O is the centre of a circle. Two tangents segments BM and BR, are drawn from external ‘point B’ to the circle at M and R respectively.
Prove that : BM = BR.
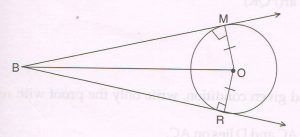
(write only the proof with reasons)
Proof:
Tangents BM and BR are perpendicular to the radii MO and RO at M and R respectively
∠BMO = 90° and ∠BRO = 90°
In right Δs BMO and BRO
Hyp BO = Hyp BO ( common side)
MO = RO ( radii of the same circle)
ΔBMO ≅ ΔBRO ( RHS )
BM = BR ( c.p.c.t)
( C) Draw line segment RS of length 7.5 cm. Taking R as centre and radius 3 cm, draw a circle. Using a pair of compass and ruler, construct two tangents SM and SN to the circle. Measure and state the length of the tangent segments.
Ans :
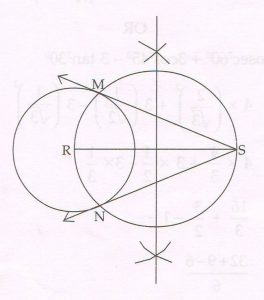
The length of each tangent segment is 6.7 cm
( D) Using a pair of compass and ruler construct ΔPQR with sides QR = cm, PQ =5.5 cm , and ∠PQR = 60°. Then construct Δ P’ QR’ whose sides are \frac{5}{3} of the corresponding sides of Δ PQR.
Ans :
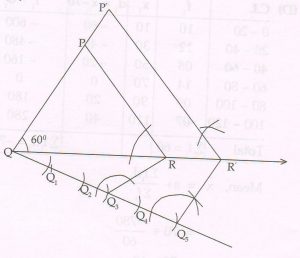
6 (A) Select and write the most appropriate alternative from those provided in the bracket :
If Sin B = Cos (2B − 30 ) where 2B is an acute angle then the value of B = _____.
[ 20° , 30° , 40° , 90° ]
Ans : 20°
(B ) Attempt ANY ONE of the following :
1. In ΔMTR , ∠T = 90° and sin R = \frac{24}{25} then find:
(a) The length of TR.
(b) The value of cot M.
(c) The value of sec R.

Ans : (a) In right ΔMTR, by Pythagoras’ theorem
TR2 + TM2 = MR2
TR2 + 242 = 252
TR2 = 625 − 576
= 49
TR = \sqrt{49}
= 7
(b) cot M = \frac{MT}{RT}
= \frac{25}{7}
(c) sec R = \frac{RM}{RT}
= \frac{25}{7}
OR
(B) Evaluate the following expression using numerical values of trigonometrical ratios.
4 cosec2 60° + 3 cos2 45° − 3 tan2 30°
Ans : 4 cosec2 60° + 3 cos2 45° − 3 tan2 30°
4 × \big( \frac{2}{ \sqrt{3} } \big)² + 3 \big( \frac{1}{ \sqrt{2} } \big)² − \big( \frac{1}{ \sqrt{3} } \big)²
= 4 × \frac{4}{3} + 3 \frac{4}{3} − 3 × \frac{1}{3}
= \frac{16}{3} + \frac{3}{2} − 1
= 32 + 9 − \frac{6}{6}
= \frac{35}{6}
( C) Prove the following identity.
Tan2 Ø+ cot2 Ø = sec2 Ø. cosec2 Ø − 2
Ans : L.H.S. = tan2 Ø + cot2 Ø
= sec2 Ø − 1 + cosec2 Ø − 1
= \frac{1}{cos² Ø } + \frac{1}{sin² Ø}− 2
= sin2 Ø + \frac{cos² Ø}{cos² Ø sin² Ø}− 2
= \frac{1}{cos² Ø sin² Ø} − 2
= \frac{1}{cos² Ø sin² Ø} . \frac{1}{sin² Ø} − 2
= sec2 Ø . cosec2Ø − 2
= R. H. S.
( D) Attempt each of the following :
1. If P ( 4, 2), Q ( 14, 5 ) and R ( 6 , 4 ) are the vertices of Δ PQR,
find the area of ΔPQR.
Ans :
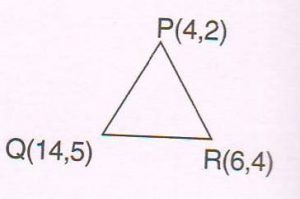
Area of a Δ PQR = \frac{1}{2} [ x1 ( y2− y3 ) + x2 ( y3 − y1 ) + x3 ( y1 − y2 ]
= \frac{1}{2} [ 4 ( 5 − 4) + 14 ( 4 − 2) + 6 ( 2 − 5) ]
= \frac{1}{2} [ 4 1 + 14 2 + 6 ( − 3 ) ]
= \frac{1}{2} [ 4 + 28 − 18 ]
= \frac{1}{2} × 14
= 7 square units
2. If AD is the median of ΔABC, whose vertices are A ( − 2, 6 ) , B (2 , 1) and C ( 8 , 7 ), find the length of median AD.
Ans :
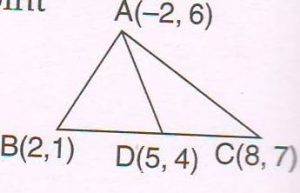
Coordinates of midpoint D =
\frac{(2 + 80)}{2} , \frac{(1 + 7)}{2}
= ( 5 , 4 )
AD = \sqrt{ (-2 -5)^{2} + (6 - 4)^{2} }
= \sqrt{49} + 4
= \sqrt{53 }
7 (A) Select and write the most appropriate alternative from those provided in the bracket :
If Δ DEF ∼ ΔPQR and \frac{EF}{QR}
=\frac{25}{4}then \frac{ar(DEF)}{ar(PQR)} = ____.
[ \frac{5}{2} , \frac{625}{16} , \frac{25}{64} , \frac{16}{625} ]
Ans : \frac{625}{16}
(B) With reference to the given figure and given condition, write only the proof with reasons of the following theorem.
Given: In ΔABC, ∠ABC = 90° , BD ⊥ AC and D lies on AC.
To prove : AC2 = AB2 + BC2
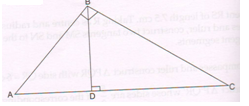
Proof:
By Similarity theorem, ΔADB ∼ ΔABC
\frac{AD}{AB} = \frac{AB}{AC} (sides are proportional )
AD . AC = AB2 … (1)
Also, ΔBDE ΔABC (from above)
\frac{DC}{BC} = \frac{BC}{AC}
DC . AC = BC2 … (2)
Adding (1) and (2),
1. AC + DC . AC = AB2 + BC2
( AD + DC) . AC = AB2 + BC2
AC . AC = AB2 + BC2
AC2 = AB2 + BC2
(C ) In the given figure, ABCD is a parallelogram. AQ and DC are produced to E. P is a point on AD, such that PQ \| DE .
Prove that : AE × BA × PD = DE × AP × QE.
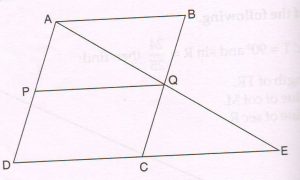
Proof :
Since PQ \| DE , by basic proportionality theorem,
\frac{AP}{PD} = \frac{AQ}{QE}
AQ × PD = AP × QE … (1)
In ΔAPQ and ΔADE
∠A = ∠A ( common angle )
∠APQ = ∠ADE ( corresponding∠s formed by PQ \| DE )
ΔAPQ ∼ ΔADE ( A.A similarity)
\frac{PQ}{DE} = \frac{AQ}{AE} (corresponding sides are proportional)
PQ × AE = AQ × DE … (2)
From (1) and (2),
AQ × PD × BA × AE = AP × QE × AQ × DE
AE × BA × PD = DE × AP × QE
( D) Two lamp posts AB and CD stand on a levelled ground and are of equal heights. A boy measured the elevation of the top of lamp post AB from the midpoint M of the line segment joining the feet of the lamp posts as 30°. After walking 15 meters towards lamp post CD he measured the elevation of its top as 60°. Find the distance between the lamp posts.
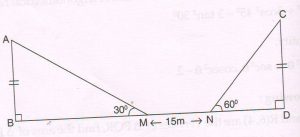
Ans : Let BM = x meters
BD = 2x meters (since M is the midpoint of BD )
Since MN = 15 meters
ND = ( x − 15 ) meters
In rt ΔABM, tan 30° = \frac{AB}{x}
\frac{1}{ \sqrt{3} } = \frac{AB}{x}
AB = \frac{x}{ \sqrt{3} } … (1)
In right ΔCDN, tan 30° = \frac{CD}{ND}
\sqrt{3} = \frac{CD}{x − 15} … (2)
Now, it is given that AB = CD
From (1) and (2) ,
\frac{x}{ \sqrt{3} } = \sqrt{3} ( x − 15 )
x = 3 ( x − 15 )
x = 3x − 45
45 = 3x − x
2x = 45
x = \frac{45}{2}
= 22.5
Distance between the lamp posts
= BD = 2x
= 2 × \frac{45}{2}
= 45 meters.
8 (A) Select and write the most appropriate alternative from those provided in the bracket :
1. The circumference of a circle is 132 cm. therefore its radius is ____cm.
[ Take π = \frac{22}{7} )
[ 84 , 42 , 21 , 10.5 ]
Ans : 21
2. The volume of a sphere of radius 1 cm is _____ cm3.
[ \frac{4}{3} π , \frac{4}{3} π2 , \frac{4}{3} π3 , \frac{4}{3} π4 ]
Ans : \frac{4}{3} π
(B ) Attempt each of the following :
1. Find the area swept by the minute hand of a clock in 20 minutes if the length of the minute hand is 9 cm. Do not substitute the value of π.
Ans : The area swept in 20 minutes
=\frac{Ø}{360} πr2
= \frac{120}{360} × π × 9 × 9 cm2
= 27 π cm2
2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The outer diameter of the hemisphere is 12 cm and the height of the vessel is 13 cm, as shown in the figure. Find the outer curved surface area of the cylindrical part of the vessel.
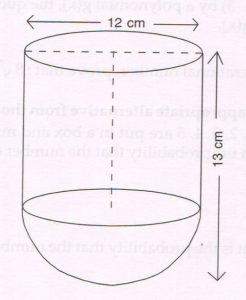
Ans : The outer curved surface area of the cylindrical part
= 2 πr h
= 2 × π × 6 × (13 − 6) cm2
= 12 π × 7 cm2
= 84 π cm2
( C) A wire when bent in the form of an equilateral triangle, encloses an area of 121 \sqrt{3} cm2 . If the same wire is bent in the form of a circle, find the area of circle. ( Take π = \frac{22}{7} )
Ans : Let s cm be the side of the equilateral triangle
∴ Area of equilateral triangle
= \frac{ \sqrt{3} }{4} S2
121 \sqrt{3} = \frac{ \sqrt{3} }{4} S²
S² = 121 × 4
S = \sqrt{121} × 4
= 11 × 2
= 22 cm
Length of the bent wire = 3s
= 3 × 22 cm
= 66 cm
2 π r = 66
2 × \frac{22}{7} π = 66
r = 66 × \frac{22}{7} × 22
= \frac{21}{2}
= 10.5 cm
Area of the circle = π r2
= \frac{22}{7} × \frac{21}{2} × \frac{22}{1}
= \frac{639}{2} cm2
= 346.5 cm2
(D ) Lead spheres of diameter 6 cm are dropped into a beaker containing some water and are fully submerged. If the inner diameter of the beaker is 18 cm, find how many lead spheres have been dropped in it the water level is raised by 40 cm. ( Take π = \frac{22}{7} )
Ans : Let the number of lead spheres be n
Volume of the n spheres submerged = the volume of the water displaced in the cylindrical shape.
n × \frac{4}{3} π r3 = π R2 H
Where r = radius of the sphere
= \frac{1}{2} × 6
= 3 cm
R = radius of the beaker
= \frac{1}{2} × 18
= 9cm
H = height of water risen
= 40 cm
n = \frac{4}{3} × π × 3 × 3 × 3 = π × 9 × 9 × 40
n = 9 × 9 × \frac{40}{4} × 3 × 3 = 90
Number of lead spheres fully submerged is 90.