Goa Board Paper March 2015
1 (A) Select and write the most appropriate alternative from those provided in the bracket :
The product of two numbers is 768 and their L.C.M. is 96. Therefore their HCF is _____.
[ 3 , 8 , 24 , 16 ]
Ans : 8
(B) Attempt the following :
(i). Find the sum of the zeros of the quadratic polynomial 3x2 + 7x + 5.
Ans : Sum of the zeros = − \frac{b}{a} = − \frac{7}{3}
(ii). Find the zeros of the quadratic polynomial x2 − 169.
Ans: Zeros are given by x2 − 169 = 0
x2 = 169
x2 = ± \sqrt{169}
= ± 13
Zeros are − 13 and 13
(C) If two zeros of the polynomial 2x4 + 5x3− 13x2 − 25x + 15 are and − \sqrt{5} , find the other zeros of the polynomial.
Ans : Two zeros are \sqrt{5} and − \sqrt{5}
Factors are x − \sqrt{5} and x + \sqrt{5}
( x − \sqrt{5} ) ( x + \sqrt{5} ) = x2 − 5
Let us divide 2x4 + 5x3 − 3x2 − 25x + 15 by x2 − 5

Other factor will be 2x2 + 5x − 3
Other zeros are given by 2x2 + 5x − 3 = 0
( 2x − 1) ( x + 3 ) = 0
2x − 1 = 0 and x + 3 = 0
x = \frac{1}{2} and x = − 3
Other zeros are \frac{1}{2} and − 3
(D) Assuming that \sqrt{7} is an irrational number, prove that 3 \sqrt{7} + 4 is also an irrational number,
Ans : Let us assume, to the contrary, that 3 \sqrt{7} + 4 is a rational number.
We can find integers a and b , both coprime ( b ≠ 0 )
Such that 3 \sqrt{7} + 4 = \frac{a}{b}
3 \sqrt{7} = \frac{a}{b} − 4
3 \sqrt{7} = a − \frac{4b}{b}
\sqrt{7} = a − \frac{4b}{3b}
Since a and b are integers a − \frac{4b}{3b} is a rational number.
But this contradicts the given condition that \sqrt{7} is irrational.
Our assumption that 3 \sqrt{7} + 4 is a rational number is wrong.
3 \sqrt{7} + 4 is irrational
2 (A) Select and write the most appropriate alternative from those provided in the bracket :
A die is tossed once. Therefore the probability of getting a number less than 3 on the top face of the die is ____.
[ \frac{1}{6} , \frac{1}{3} , \frac{2}{3} , \frac{1}{2} ]
Ans : \frac{1}{3}
(B) Cards marked with numbers 3 , 4 , 5 , ………50, are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that the number on the drawn cardis
(i). Divisible by 6.
Ans : Number divisible by 6 are 6 , 12 , 18 , 24 , 30 , 36 , 42 , 48.
So altogether we have 8 numbers
Probability of getting a number card divisible by 6
= \frac{favourable \thinspace \thinspace outcomes}{all \thinspace \thinspace possible \thinspace \thinspace outcoms}
= \frac{8}{48}
= \frac{1}{6}
(ii). A single digit number.
Ans : Single-digit numbers will be 3 , 4 , 5 , 6 , 7 , 8 , 9
So altogether we have 8 numbers
Probability of getting a single-digit number card
= \frac{favourable \thinspace \thinspace outcomes}{all \thinspace \thinspace possible \thinspace \thinspace outcoms}
= \frac{7}{48}
(C) Find the roots of ANY ONE of the following :
1. 2x2 + 3x − 27 = 0
( By factorization method )
Ans : 2x2 + 3x − 27 = 0
2x2– 6x + 9x − 27 = 0
2x (x − 3 ) + 9 (x − 3 ) = 0
( x − 3 ) (2x + 9 ) = 0
Either x − 3 = 0 or 2x + 9 = 0
x = 3 or x = − \frac{9}{2}
Roots of the equation are 3 and − \frac{9}{2}
2. 3x2 + 6x + 1 = 0 (deleted portion)
( By completing the square method )
Ans : 3x2 + 6x + 1 = 0
Multiplying by 3, we get
9x2 + 18x + 3 = 0
(3x)2 + 2 × 3x × 3 + 32 − 32 + 3 = 0
( 3x + 3 )2 − 9x + 3 = 0
( 3x + 3)2 = 6
3x + 3 = ± \sqrt{6}
3x = − 3 ± \sqrt{6}
x = − 3 ± \frac{ \sqrt{6} }{3}
Roots are − 3+ \frac{ \sqrt{6} }{3} and − 3 − \frac{ \sqrt{6} }{3}
Or − 1 + \frac{ 1}{3 \sqrt{6} } and − 1 − \frac{ 1}{3 \sqrt{6} }
(D) Two cyclists start from the same point, at the same time. One goes due north and the other due west, along straight highways. Also, the speed of one cyclist is 5 km/ h more than the other. If after two hours, they are 50 km apart from each other, find the average speed of each cyclist.
Ans :
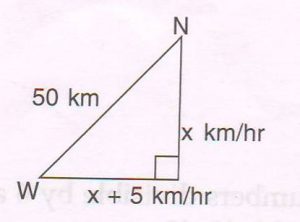
Let the speed of one cyclist be x km/ hr
The speed of the other cyclist will be ( x + 5 ) km/hr
Since Distance = Speed × Time
After 2 hours the distance covered by them are respectively,
2x km and 2 ( x + 5 ) km
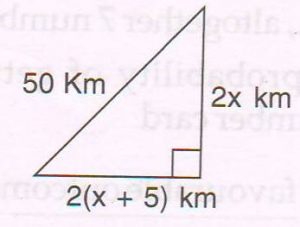
They are 50 km apart. So by Pythagoras theorem,
( 2x)2 + [ 2 ( x + 5) ]2 = 502
4x2 + 4x2 + 40x + 100 − 2500 = 0
8x2 + 40x − 2400 = 0
Dividing by 8 x2 + 5x − 300 = 0
x2 + 20x − 15x − 300 = 0
x (x + 20 ) − 15 ( x + 20 ) = 0
(x + 20 )( x − 15 ) = 0
x + 20 = 0 or x − 15 = 0
x = − 20 or x = 15
Since speed is not negative − 20 is omitted.
x = 15
Speed of one cyclist is 15 km / hr
And that of the other is 15 + 5 = 20 km / hr
3 (A) Select and write the most appropriate alternative from those provided in the brackets :
If 13x + 12 y = 7 and 12x + 13 y = 5 then x −y = ____.
[ − 12 , − 2 , 12 , 2 ]
Ans : 2
(B) A two-digit number is such that the sum of its digits is 9. If the difference of the number obtained by reversing the digits and the original number is 9, then write down two equations in x and y to represent the above statements.
Ans : Let the digit in the ten’s place be x
And the digit in the unit’s place be y
The number with reversed digits is 10y + x .
The two equations are
x + y = 9 … (1)
And ( 10y + x) − ( 10x + y ) … (2)
(C) Find the solution of ANY ONE of the following :
1. 7x + 11y = 3 and 8x + y = 15
(By elimination method)
Ans : 7x + 11y = 3 …. (1)
8x + y = 15 …. (2)
Multiply eq. (2) by 11,
88x + 11y = 165 …. (3)
7x + 11y = 3 …. (1)
− − −
___________________
81x = 162
Subtracting x = \frac{162}{81}
x = 2
Substituting x = 2 in eq . (2),
We get 8 × 2 + y = 15
y = 15 − 16
y = − 1
The solution is x = 2, y = − 1
2. 4x + y = 14 and 5x + 6y = 27
( By cross multiplication method )
Ans : 4x + y − 14 = 0 … (1)
5x + 6y − 27 = 0 …. (2)
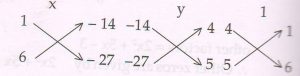
\frac{x}{- 27 −(- 84)} = \frac{y}{- 70 − (- 108)} = \frac{1}{24 − 5}
\frac{x}{− 27 + 84} = \frac{y}{− 70 + 108} = \frac{1}{19}
x =\frac{57}{19} and y = \frac{38}{19}
x = 3 and y = 2
Solution is x = 3 , y = 2
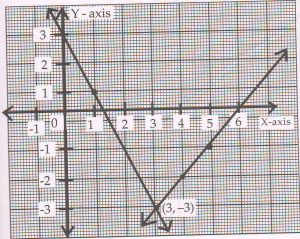
(D) Solve the following pair of linear equations graphically.
2x + y = 3 and x − y = 6
Rewrite and complete the following tables. Plot at least three points for each line using graph paper.
2x + y = 3
|
x |
|
|
|
|
y |
|
|
|
x- y = 6
|
x |
|
|
|
|
y |
|
|
|
Ans : 2x + y = 3
|
x |
0 |
1 |
2 |
|
Y = 3 − 2x |
3 |
1 |
− 1 |
x − y = 6
|
x |
4 |
5 |
6 |
|
y = x − 6 |
− 2 |
− 1 |
0 |
Graphical solution is x = 3, y = − 3
4 (A) Select and write the most appropriate alternative from those provided in the brackets :
The 19th term of an A.P. : 3 , 8 , 13 , 18 …… is _____.
[ 99 , 93 , 77 , 88 ]
Ans : 93
(B) The annual profits earned by 30 shops of a shopping complex in a locality are given as follows:
|
Profits in (Rs) lakhs ( C.I.) |
Number of shops (fi) |
|
4 − 6 |
7 |
|
6 − 8 |
5 |
|
8 − 10 |
10 |
|
10 −12 |
8 |
Find the median of the above data.
Ans : n = 30
\frac{n}{2} = 15
8 − 10 is the median class
Median = l + ( \frac{n}{2} − \frac{cf}{f} )× h
= 8 + [ 15 − \frac{12}{10} ] × 2
= 8 + ( \frac{3}{10}) × 2
= 8 + \frac{6}{10}
= 8.6
(C) John buys a T.V worth Rs 40,500 in 12 monthly installments. He pays Rs 5000 as his first installment and after that, each installment is Rs 150 less than the previous month.
Find the total amount he pays for the T.V by installments. Also, calculate the extra amount paid by him.
Ans : a = 5000 , n = 12 , d = − 150
Total amount paid by instalments is given by
S = \frac{n}{2} [ 2a + ( n − 1 ) d ]
= \frac{12}{2} [ 2 × 5000 + ( 12 − 1 ) ( − 150) ]
= 6 [ ( 10,000 + 11 ( − 150 ) ]
= 6 [ 10,000 − 1650 ]
= 6 × 8350
= 50,100
Total amount is Rs 50,100
Extra amount paid
= Rs ( 50,100 − 40,500 )
= Rs 9600
(D) The table below shows the marks obtained by the students in a Maths test;
Taking class mark ( denoted by a) of the class interval (40 − 50 ) as assumed mean, rewrite and complete the table and find the mean of the data.
Ans :
|
C.I. |
fi |
xi |
di =xi − 45 |
Fi di |
|
20 − 30 |
5 |
25 |
– 20 |
− 100 |
|
30 − 40 |
10 |
35 |
− 10 |
− 100 |
|
40 − 50 |
9 |
[45] |
0 |
0 |
|
50 − 60 |
12 |
55 |
10 |
120 |
|
60 − 70 |
8 |
65 |
20 |
160 |
|
70 − 80 |
6 |
75 |
30 |
180 |
|
Total |
∑ fi = 50 |
|
|
∑fidi = 260 |
Mean of the data = a + \frac{∑fidi }{∑fi}
= 45 + \frac{260}{50}
= 45 + 5.2
= 50.2.
5 (A) Select and write the most appropriate alternative from those provided in the bracket :
PT is a tangent from point P to the circle with center ‘O’ at T. If OP = 13 cm and PT = 12 cm. Then the diameter of the circle is ____cm
[ 5 , 10 , 25 , 15 ]
Ans : 10
(B) In the figure given below, A is a point in the exterior of the circle with center‘ O’. AP and AQ are two tangents to the circle at P and Q respectively.
Prove that: AP = AQ.
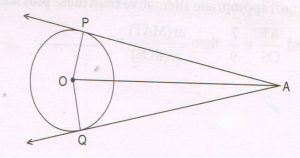
( Write only the proof with reasons)
Proof: Tangents at P and Q are perpendicular to the radii at those points
AP ⊥ OP at P and AQ ⊥ OQ at Q
In right triangles OPA and OQA
OP = OQ ( radii of the same circle)
OA = OA ( common side )
ΔOPA ≅ ΔOQA ( RHS theorem )
AP = AQ ( c.p.c.t )
(C ) Draw a circle with center O and radius 3.5 cm. Then take a point S at a distance of 7.5 cm from the center of the circle. Using a pair of a compass and ruler only, construct two tangents SV and ST the circle. Measure and state the length of the tangent segments.
Ans :
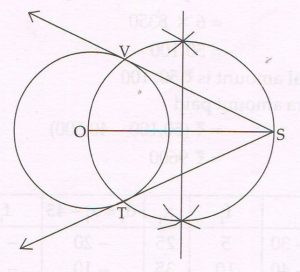
The length of each tangent segment is 6.5 cm
(D) Using a pair of compass and ruler only, construct D ABC such that BC = 5 cm, CA = 6 cm and AB = 7 cm. Then construct Δ AB’C similar to Δ ABC whose sides are \frac{3}{4} of the corresponding sides of ΔABC.
Ans :
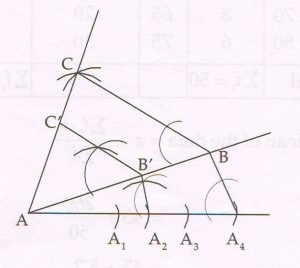
ΔAB’C’ is the required triangle.
6 (A) Select and write the most appropriate alternative from those provided in the bracket :
If Sin 2A = cos ( A + 30 ) where 2A is an acute angle, then A = _____.
[ 10° , 20° , 40° , 30° ]
Ans : 20°
(B) Attempt ANY ONE of the following :
1. In ΔPQR, ∠Q = 90° and cos R = \frac{21}{29} Then find:
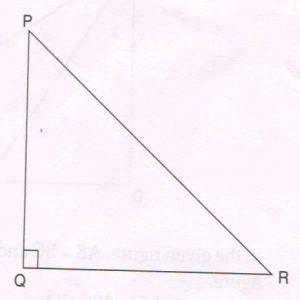
(a) The length of PQ
(b) The value of cot P
(c) The value of cosec R
Ans : In right. ΔPQR, by Pythagoras theorem
(a) PQ2 + QR2 = PR2
PQ2 + 212 = 292
PQ2 = 841 − 441
PQ2 = 400
PQ² = \sqrt{400} = 20
(b) cot P = \frac{1}{tanP} = \frac{1}{ \frac{21}{20} } = \frac{20}{21}
(c) cosec R = \frac{1}{sin R} = \frac{1}{ \frac{20}{29} } = \frac{29}{20}
2. Evaluate the following expression using numerical values of trigonometrical ratios.
4 tan2 30° + cosec2 60° − \frac{1}{sec² 45°}
Ans : 4 tan230 + cosec2 60 − \frac{1}{sec² 45°}
= 4 ( \frac{1}{ \sqrt{3} } )2 + ( \frac{1}{sin 60} )2– cos2 45
= \frac{4}{3} + \frac{1}{ \frac{ \sqrt{3} }{2} }² – ( \frac{1}{ \sqrt{2} } )2
= \frac{4}{3} + \frac{4}{3} − \frac{1}{2}
= \frac{8}{3} − \frac{1}{2}
= 16 − \frac{3}{6}
= \frac{13}{6}
(C) Prove the following identity :
Sin2 Ø [ \frac{1}{1 - cos Ø } + \frac{1}{1 + cos Ø } ] = 2
Ans : L.H.S. = sin Ø \big( \frac{1}{1 - cos Ø } + \frac{1}{1 + cos Ø } \big)
= sin² Ø \big( \frac{1 + cos Ø + 1 - cos Ø}{(1 - cos Ø ) ( 1 + cos Ø)} \big)
= sin² Ø ( \frac{2}{1 − cos² Ø} )
= sin² Ø ( \frac{2}{sin² Ø} )
= 2 = R.H.S.
(D) Attempt the following :
1,. Find the area of the triangle formed by the points, R (4 ,− 3), S (2 , 5 ) and T ( − 3, 4)
Ans :
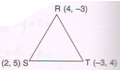
Area of ΔRST = \frac{1}{2} [ x1 (y2 − y3) + x2 (y3 − y1) + x3 (y1 − y2 ) ]
= \frac{1}{2} [ 4 ( 5 − 4) + 2 ( 4+ 3) + (− 3) ( − 3 − 5) ]
= \frac{1}{2} [ 4 ×1 + 2 × 7 − 3 × ( – 8) ]
= \frac{1}{2} [ 4 + 14 + 24 ]
= \frac{1}{2} × 42
= 21 sq. units
2. The midpoints of sides AB and AC of Δ ABC are D ( − 4, 7) and E (2 , − 1) respectively. Find the length of side BC of ΔABC.
Ans : let A = ( x1 , y1 )
B = ( x2 , y2 )
And C = ( x3 , y3 )
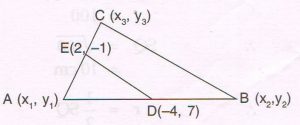
x1 + \frac{ x_{2} }{2} = − 4 x1 + x2 = − 8
And x1 + \frac{ x_{3} }{2} = 2 x1 + x3 = 4
Subtracting, we get x2− x3 = − 12 …. (1)
Also y1 + \frac{ y_{2} }{2} = 7 y1 + y2 = 14
Ans y1 +\frac{ y_{3} }{2}= − 1 y1 + y3 = − 2
Subtracting, we get y2 − y3 = 16 …. (2)
BC = \sqrt{( x_{2}- x_{3)²} + ( y_{2}- y_{3)²} }
= \sqrt{( -12)² + 16²} using (1) and (2)
= \sqrt{144 + 256}
= \sqrt{400}
= 20
7 (A) Select and write the most appropriate alternative from those provided in the bracket :
If D MAT D ROS and AT / OS = 7/9 then ar( MAT) / ar (ROS) = _____.
( \frac{ \sqrt{7} }{3} , \frac{ 3}{ \sqrt{7} } , \frac{81}{49} , \frac{49}{81})
Ans : \frac{49}{81}
(B) With reference to the given figure and given condition, write only the proof with reasons of the following theorem.
Given : In Δ XYZ, X − L − Y , X − M − Z and MT ⊥ XY.
To prove : =\frac{XL}{LY} = \frac{XM}{MZ}
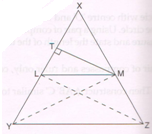
Proof: Let LS ⊥ XZ
Area of a triangle = \frac{1}{2} × base × height
\frac{ar ( XLM)}{ar ( YLM)}
= \frac{ \frac{1}{2} × XL × MT }{ \frac{1}{2} × YL × MT }
= \frac{XL}{YL} …. (1)
And
\frac{ar ( XLM)}{ar ( ZLM)}
= \frac{ \frac{1}{2} × XL × MT }{ \frac{1}{2} × YL × MT }
= \frac{XL}{YL} …. (2)
Now Δ YLM and Δ ZLM are on the same base YZ and between the same parallels LM and YZ
ar ( YLM) = ar ( ZLM) …. (3)
From (1) , (2) and (3) we get
\frac{XL}{YL} = \frac{XM}{ZM}
∴ \frac{XL}{LY} = \frac{XM}{MZ}
(C)
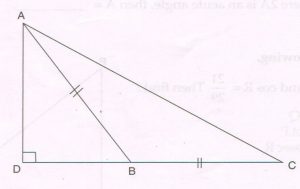
In the given figure, AB = BC and AD is drawn perpendicular to CB produced at D, as shown in the figure.
Prove that : AC2 = 2BC.CD
Ans : L.H.S = AC2
= AD2 + DC2( by Pythagoras theorem)
= ( AB2− DB2) + DC2 ( by Pythagoras theorem )
= BC2– − DB2 + (DB + BC)2( AB = BC)
= BC2 − DB2 − DB2 + 2DB.BC + BC2
= 2BC2 + 2DB.BC
= 2BC ( BC + DB)
= 2BC.CD
= R. H .S
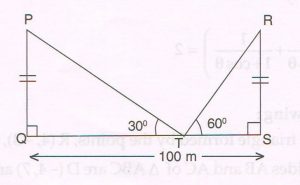
(D) Two towers PQ and RS of equal height are standing opposite each other on a levelled ground and the distance between them is 100 m. From a point T between them on the ground, the angle of elevation of their tops ‘P’ and ‘R’ are 30° and 60° respectively, as shown in the figure. Find the height of each tower and the distance of the point T from the tower PQ
Ans : Let PQ = RS = x meters
And QT = y meters
TS = ( 100 − y ) meters
In right Δ PQT, tan 30° = \frac{PQ}{QT}
\frac{1}{ \sqrt{3} } = \frac{x}{y}x = \frac{y}{ \sqrt{3} } …. (1)
Also in right Δ RST,
Tan 60° = \frac{RS}{TS}
\sqrt{3}
= \frac{x}{100 − y}100 \sqrt{3} − y \sqrt{3}
= x …. (2)
From (1) and (2),
100 \sqrt{3} − y \sqrt{3}
= \frac{y}{ \sqrt{3} }
300 − 3y = y
4y = 300
y = \frac{300}{4} = 75
x = \frac{y}{ \sqrt{3} } = \frac{75}{ \sqrt{3} }
= \frac{75}{ \sqrt{3} } × \frac{ \sqrt{3} }{ \sqrt{3} }
= \frac{75 \sqrt{3} }{3 }
= 25 \sqrt{3}
The height of each tower is 25 meters and the distance of point T from the tower PQ is 75 meters.
8 (A) Select and write the most appropriate alternative from those provided in the bracket :
1. If the angle of a sector is 60° and its radius is 6 cm, then the area of the sector is ___ cm2.
[ π , 2 π , 6 π , 36 π ]
Ans : 6 π
2. If the height of a cubical tank is 1.5 meters, then its volume is ____ m3
[ 2.25 , 3 , 3.375 , 4.5 ]
Ans : 3. 375
(B) Attempt each of the following :
1. In the following figure EYF and GXH are arcs of two concentric circles with center O and radii 5 cm and 8 cm respectively. If ∠ EOF = 30°, then find the length of arc EYF.
( Do not substitute the value of π )
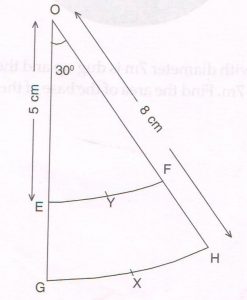
Ans : Length of arc EYF = \frac{Ø}{360} × 2 π r
= \frac{30}{360} × 2π × 5 cm
= \frac{5 π}{6} cm
2. A hemispherical depression is scooped out from one face of a cubical wooden block of edge 5 cm such that the diameter of the hemisphere is equal to the edge of the cube, then find the inner curved surface area of the hemispherical depression.
( Do not substitute the value of π )
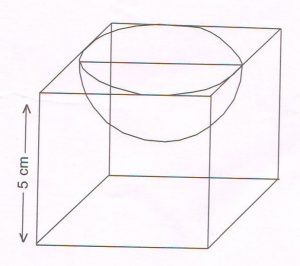
Ans : The inner diameter = \frac{1}{2} × 5cm = 2.5 cm
The inner curved surface area of the hemispherical depression
= \frac{1}{2} × 4 π r2
= 2π × 2.5 × 2.5 cm2
= 12.5 π cm2
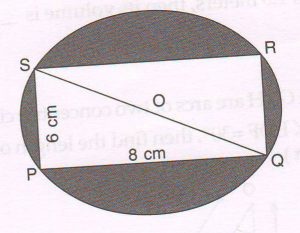
(C) In the following figure, rectangle PQRS is inscribed in a circle with center‘ O’. If PQ = 8 cm and PS = 6 cm, find the area of the shaded portion.
( Take π = 3.14)
Ans : SQ2 = PQ2 + PS2 ( by Pythagoras theorem)
= 82 + 62
= 64 + 36
= 100
SQ = \sqrt{100}
= 10 cm
r = \frac{1}{2} SQ
= \frac{1}{2} × 10 cm
= 5 cm
Area of the circle = π r2
= 3. 14 × 5 × 5 cm2
= 78.5 cm2
Area of rectangle PQRS
= PQ × PS
= 8 × 6 cm2
= 48 cm2
Area of the shaded region
= ( 78.5 − 48 ) cm2
= 30.5 cm2
(D) A 16 m deep well with a diameter of 7 m is dug up and the earth is evenly spread out to form a cuboidal platform of height 7 m. Find the area of the base of the cuboidal platform.
( Take π =\frac{22}{7} )
Ans : Volume of the 16m deep well = Volume of the cuboidal platform
π r2h = area of the base × height
\frac{22}{7} ×\frac{7}{2} × \frac{7}{2}× 16 = area of the base of the cuboid × 7
Area of the base of the cuboid
= \frac{22}{7} × \frac{4}{7}
= 88m2