SAMPLE PAPER MATHEMATICS OCTOBER 2013
1 (A) Select and write the most appropriate alternative from those provided in the bracket :
If two coins are tossed simultaneously, then the probability of getting at least one head is _____.
[ \frac{1}{4} , \frac{1}{2} , \frac{3}{4} , 1 ]
Ans : \frac{3}{4}
(B) A deck of 52 playing cards is well shuffled. If only one card is drawn from the deck of cards at random, find the probability of getting :
1. A black coloured card
Ans : All possible outcomes = 52
Favourable outcomes = 26
Probability of getting a black coloured card
= \frac{26}{52} = \frac{1}{2}
2. A face card
Ans : All possible outcomes = 52
There are 12 face cards
Favourable outcomes = 12
Probability of getting a face card
= \frac{12}{52} = \frac{3}{13}
(C) Find the roots of ANY ONE of the following quadratic equations :
1. 6x2− 11x − 10 = 0
(By Factorisation Method)
Ans : 6x2 − 11x − 10 = 0
6x2 + 4x − 15x − 10 = 0
2x (3x + 2) − 5 (3x + 2) = 0
(3x + 2) (2x − 5) = 0
Either 3x +2 = 0 OR 2x − 5 = 0
3x = − 2 OR 2x = 5
x = − \frac{2}{3} OR x = \frac{5}{2}
The roots are − \frac{2}{3} and \frac{5}{2} .
2. 2x2 + 5x − 3 = 0
(By Quadratic Method)
Ans : Using Quadratic formula method:
(i) We have, 2x2 + 5x − 3 = 0
Here, a = 2, b = 5 and c = − 3
Therefore, D = \sqrt{b}² – 4ac
D = \sqrt{(5)}² – 4 × 2 × − 3 = \sqrt{25} + 24 = \sqrt{49}
D = 7
D > 0, roots exist.
Roots are given as x = (− b ± \frac{ \sqrt{D} }{2 a} )
= − 5 ± \frac{ \sqrt{49} }{2 × 2 }
= \frac{( − 5 ± 7)}{4}
= \frac{( − 5 + 7)}{4} OR \frac{( − 5 − 7)}{4}
= \frac{2}{4} OR − \frac{12}{4}
x = \frac{1}{2} OR − 3
(D ) An express Kadamba bus takes 1 hour less than an ordinary bus to travel a distance of 180 km from Karwar to Sawantwadi. If the average speed of the express Kadamba bus is 15 km/h more than that of the ordinary bus, find the average speed of the ordinary bus.
Ans : Let the average speed of the ordinary bus be x km/hr
Time taken to cover 180 km is 180/x hours … (1)
Since a Kadamba bus takes 1 hr less,
Time taken by a Kadamba bus to cover the same distance is
( \frac{180}{x − 1} )hours
If the average speed of a Kadamba bus is made ( x + 15) km/hr
Then to cover 180 km, it will take the time of
\frac{180}{x + 15} hours. … (2)
(1) and (2) being equal we get,
\frac{180}{x − 1} = \frac{180}{x + 15}
180 (x + 15) − x (x + 15) = 180 x
180x + 2700 – x2 – 15x = 180x
x2 + 15 x − 2700 = 0
(x + 60) (x − 45) = 0
x + 60 = 0 OR x − 45 = 0
x = − 60 OR x = 45
Since speed x cannot be a negative number
− 60 is discarded.
x = 45
Average speed of the ordinary bus is 45 km/hr
2(A) Select and write the most appropriate alternative from those provided in the bracket :
If 4x + y = 7 and x + 4y = − 2, then the value of x − y= _____.
[ 1 , 3 , 5 , 9 ]
Ans : 3
(B) The following is a pair of linear equations :
2x + 3y − 6 = 0
( k +1) x + (2k − 1) y = 18
Answer the following questions with reference to the given equations :
1. Write down the conditions for no solution.
Ans : \frac{2}{k + 1}
= \frac{3}{ 2k − 1} ≠ \frac{ − 6}{ − 18}
2. Find the value of k.
Ans : \frac{2}{k + 1}
= \frac{2}{ 2k − 1}
2 ( 2k − 1) = 3 ( k + 1)
4k − 2 = 3k +3
4k − 3k = 3 + 2
k = 5
(C ) Find the solution of ANY ONE of the following pairs of linear equations :
1. 5x + 7y = − 1 ; 2x − 3y = 17
(By elimination method)
Ans :
5 x + 7y = − 1 …(1)
2x − 3y = 17 …(2)
Eq. (1) × 3, 15x + 21y = − 3
Eq. (2) × 7, 14x − 21y = 119
_____________
Adding we get 29x = 116
x = \frac{116}{ 29} = 4
∴ x = 4
Substituting x = 4 in eq.(1),
We get 5 × 4+ 7y = − 1
7y = − 1 − 20
7y = − 21
y = − \frac{21}{ 7} = − 3
The solution is x = 4, y = − 3
2. 4x + y = 11 ; 7x − 2y = 8
(By substitution method)
Ans : 4x + y = 11 gives y = 11 − 4x … (1)
Substituting value of y in 7x − 2y = 8 we get
7x − 2 (11 − 4x) = 8
7x − 22 + 8x = 8
15x = 8 + 22
15x = 30
x = \frac{30}{ 15} = 2
Substituting x = 2 in eq. (1),
y = 11 − 4 × 2
= 11 – 8
= 3
The solution is x = 2, y = 3.
(D) Two years ago the age of Kamla was four times the age of her daughter. Three years hence Kamla will be three times as old as her daughter. Find the present ages of Kamla and her daughter.
Ans : Let Kamla’s age be x years
And her daughter’s present age be y years
Two years ago, Kamla’s age was (x − 2) years and daughter’s age was ( y − 2) years
By the given condition we get, x − 2 = 4 (y − 2) … (1)
Three years hence, Kamla will be (x + 3) years and her daughter will be ( y + 3) years
By the given condition we get x + 3 = 3 (y + 3) …(2)
Solving (1) and (2) ,
x − 2 = 4y − 8
x − 4y = − 6 … (3)
x + 3 = 3y + 9
x − 3y = 6 … (4)
x − 4y = − 6 … (3)
− + +
___________
y = 12
Substituting y = 12 in eq. (4), we get,
x − 3 = 6
x = 6 + 36
= 42
Kamla’s present age is 42 years and her daughter’s age is 12 years.
3 (A)Select and write the most appropriate alternative from those provided in bracket :
The L.C.M of the numbers 147 and 126 is _____.
[ 14 , 42 , 882 , 18522 ]
Ans : 882
(B) Find the zeros of the quadratic polynomial x2 − 5x + 6 and hence verify the relationship between the zeros and the coefficients.
Ans : To get zeros
x2− 5x + 6 = 0
( x − 2) (x − 3) = 0
x − 2 = 0 OR x − 3 = 0
x = 2 OR x = 3
The two zeros are 2 and 3
Sum of the zeros = 2 + 3 =5
= \frac{− (− 5)}{ 1} = \frac{− (coefficient \thinspace \thinspace of \thinspace x)}{ coeffient \thinspace \thinspace of \thinspace x²}
Product of the zeros = 2 × 3 = 6
= \frac{6)}{ 1} = \frac{− (constant \thinspace \thinspace term)}{ coeffient \thinspace \thinspace of \thinspace x²}
(C) Find the quotient and the remainder when the polynomial 2x3− 5x2 + 7x + 1 is divided by the polynomial 2x − 3. Hence, express the result in the form
Dividend = Divisor × Quotient + Remainder
Ans :
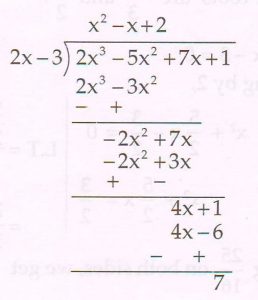
Quotient = x2 −x + 2
Remainder = 7
2x3 − 5x2 + 7x + 1 = (2x − 3) (x2 – x + 2 ) + 7
(D ) Using Euclid’s division algorithm find the H.C.F of the numbers 966 and 707.
Ans : Applying division lemma to 966 and 707 we get
966 = 707 × 1 + 259
Since the remainder is 259 we apply division lemma to
707 and 259
707 = 259 × 2 + 189
Again by division lemma,
259 = 189 × 1 + 70
Again we get,
189 = 70 × 2 + 49
70 = 49 × 1 + 21
49 = 21 × 2 + 7
21 = 7 × 3 + 0
Since the remainder is 0,
We stop our procedure .
At this step , the divisor was 7.
So the H.C.F of 966 and 707 is 7
4( A) Select and write the most appropriate alternative from those provided in the brackets :
The sum of the first ten natural numbers is _____.
[ 11 , 20 , 55 , 100 ]
Ans : 55
(B ) The following distribution gives the daily income of 60 village labourers:
|
Daily income ( in RS) |
Number of labourers |
|
120 − 150 |
3 |
|
150 − 180 |
7 |
|
180 −210 |
8 |
|
210 − 240 |
20 |
|
240 − 270 |
16 |
|
270 − 300 |
6 |
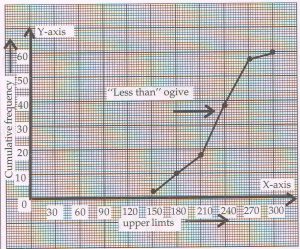
Convert the distribution above to a less than type cumulative frequency distribution and draw it is less than ogive.
Ans :
|
Daily Income (in Rs) |
Numbers of labourers |
|
Less than 150 |
3 |
|
Less than 180 |
10 |
|
Less than 210 |
18 |
|
Less than 240 |
38 |
|
Less than 270 |
54 |
|
Less than 300 |
60 |
For drawing the ogive “less than” type, we take the scale on the horizontal axis (x-axis)
1 cm = 30 units and the scale on the vertical axis ( y-axis) 1 cm = 3 = 10 units
( C) In an Arithmetic Progression consisting of 20 terms the 4th term is 29 and the last term is 125. Find the 10th term of the Arithmetic Progression.
Ans : 29 = a4 = a + (4 − 1) d
a + 3d = 29 … (1)
Also 125 = a20 = a + (20 − 1) d
a + 19d = 125 … (2)
a + 3d = 29
− − −
_____________
16 d = 96
d = \frac{96}{ 16} = 6
From (1) a + 3 = 29
a = 29 – 18
a = 11
The 10th term a10 = a + (10 − 1 )d
= 11 + 9
= 11 + 54 = 65
(D ) The table below gives the percentage distribution of female teachers in the primary schools of a certain taluka of Goa. Rewrite and complete the following table and find the mean percentage of the female teachers by using ‘Direct Method’.
Mean percentage of female teachers
= \frac{10230}{ 200}
= 51.15
5( A) Select and write the most appropriate alternative from those provided in the bracket :
If tan A = cot 32°, then the measure of ∠A is _____.
[ 16° , 32° , 58° , 148° ]
Ans : 58°
( B) Attempt ANY ONE of the following :
1. In D ABC, ∠B = 90°. If cos A =\frac{2}{ \sqrt{13} } , find
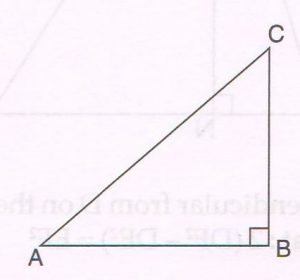
(a) The length of BC
(b) The value of tan A
(c) The value of cosec A
Ans : (a) In right ΔABC, by Pythagoras ‘ theorem
AB2 + BC2 = AC2 … (1)
Since cos A = \frac{2}{ \sqrt{13} } = \frac{AB}{ AC}
From (1) we get 22 + BC2
= ( \sqrt{13} )2 … (2),
BC2 = 13 − 4 = 9
∴ BC = \sqrt{9} = 3
(b) tan A = \frac{BC}{ AB}
= \frac{3}{ 2}
(c) coscA = \frac{1}{ sinA}
= \frac{1}{ \frac{BC}{AC} }
= \frac{AC}{ BC}
= \frac{ \sqrt{13} }{3}
2. Evaluate :
9 cos2 − 60° + sin 45° − cot2 30°.
Ans : 9 × (\frac{1}{2} )² + \frac{ \sqrt{2}× 1 }{ \sqrt{2} } − (\sqrt{3})²
= 9 × \frac{1}{ 4} + 1 − 3
= 2 + \frac{1}{ 4} − 2
= \frac{1}{ 4}
( C) Prove that :
\frac{tanA - sinA}{ tanA + sinA} = \frac{secA - 1}{ secA + 1}
Ans :
LHS = \frac{ \frac{sinA}{cosA} - sinA }{ \frac{sinA}{cosA} + sinA}
= \frac{sinA (1 - cosA) / cosA }{sinA (1 + cosA) / cosA}
= \frac{1 - cosA }{1 + cosA}
= \frac{(1 - cosA) / cosA }{(1 + cosA) / cosA}
[ Dividing Num and Den by cos A]
= \frac{ \frac{1}{cosA} - 1}{ \frac{1}{cosA} + 1 }
= \frac{secA - 1 }{secA + 1} = R.H.S.
(D) Attempt each of the following :
1. Find the distance between the points P ( 5 , 2) and Q ( − 3 , − 4).
Ans :
PQ = \sqrt{(5 + 3)² + (2 + 4)²}
= \sqrt{(8)² + (6)²}
= \sqrt{(64) + (36)}
= \sqrt{100}
= 10
2. If A (2, − 2) , B( − 2, 8) and ( − 1, − 3) are the vertices of ΔABC, find its area.
Ans : Area of Δ ABC
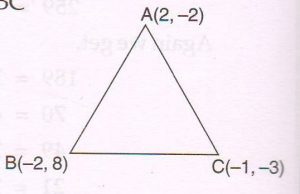
= \frac{1}{ 2} [ 2 × (8 + 3) − 2 ( − 3 + 2 ) − 1 (− 2 − 8) ]
= \frac{1}{ 2} [ 2 × 11 − 2 × ( − 1) − 1 ( −10) ]
= \frac{1}{ 2} [ 22 + 2 + 10]
= \frac{1}{ 2} × 34
= 17 square units.
6( A) Select and write the most appropriate alternative from those provided in the brackets :
ΔPQR ∼ ΔABC. If ar(PQR) = 27cm2 and BC = 10 cm, then QR = _____cm.
[ 3 , 5 , 6 , 36 ]
Ans : 6
(B) Given: D and E are the points on the sides RS and RT respectively of ΔRST such that DE \parallel ST , EM ⊥RS and DN ⊥ RT . DT and ES are joined.
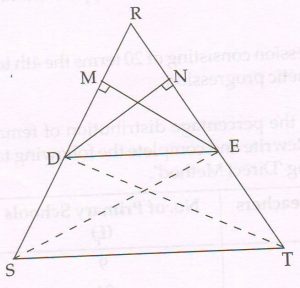
Prove that:
\frac{RD}{ DS} = \frac{RE}{ ET}
(write only the proof with reasons.)
Proof: Now ar (RDE) = ½ base × height
= ½ RD × EM
Similarly ar(DSE) = ½ DS × EM
\frac{ar (RDE)}{ ar (DSE) } = \frac{ \frac{1}{2}RD ×EM }{ \frac{1}{2}DS× EM } = \frac{RD}{ DS} … (1)
Also ar ( RDE) = ½ RE × DN
Similarly ar(DET) = ½ (ET × DN)
\frac{ar (RDE)}{ ar (DET) } = \frac{ \frac{1}{2}RE ×DN }{ \frac{1}{2}ET× DN } = \frac{RE}{ ET} … (2)
Now Δ DSE and ΔDET are on the same base DE and between the same parallels ST and DE
ar (DSE) = ar (DET) … (3)
From (1) (2) and (3), we get
\frac{RD}{ DS} = \frac{RE}{ ET}
(C)
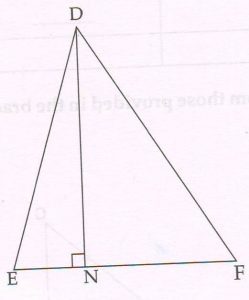
The perpendicular from D on the side EF of ΔDEF intersects EF at N such that NF = 3 EN
Prove that : 2 (DF2− DE2) = EF2
Proof:
Given NF = 3 EN
\frac{NF}{ EN} = \frac{3}{ 1}
\frac{NF + EN}{ EN} = 3 + \frac{1}{ 1}
\frac{EF}{ EN} = \frac{4}{ 1}
EN =\frac{1}{ 4} EF … (1)
So NF =\frac{3}{4} EF … (2)
Now DN2 = DE2 – EN2
(Pythagoras theorem in ΔDNE)
And DN2 = DF2 – NF2
(Pythagoras theorem in ΔDNF)
DF2 – NF2 = DE2– EN2
DF2 – DE2 = NF2– EN2
= (\frac{3}{ 4} EF)2− (\frac{1}{ 4} EF)2
=\frac{9}{ 16} EF2− \frac{1}{ 16} EF2
DF2− DE2 = \frac{8}{ 16} EF2
= \frac{1}{ 2} EF2
2 (DF2 – DE2) = EF2
(D ) Two poles AB and CD of equal heights are standing opposite to each other on either side of the road, which is 50m wide. From the top of the pole AB, the angle of depression of a point E on the road is 30° and the angle of elevation of the top of the pole CD from the point E is 60°. Find the distance of point E from the pole AB.
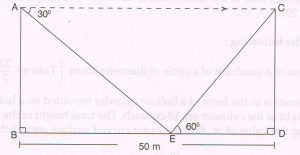
Ans : Let AB = x meters CD = x meters
Let BE = y meters ED = (50− y) meters
In right ΔCDE,
Tan 60° = \frac{CD}{ ED}
= \frac{x}{ 50 − y}
\sqrt{3}
= \frac{x}{ 50 − y}
x = \sqrt{3} (50 − y) … (1)
∠AEB =∠CAE = 30°
In right ΔABE,
Tan 30° = (\frac{AB}{ BE} = \frac{x}{ y}
\frac{1}{ \sqrt{3} } = \frac{x}{ y}
x = \frac{y}{ \sqrt{3} } …(2)
From (1) and (2)
\frac{y}{ \sqrt{3} }
= \sqrt{3} (50 − y)
y = 3 (50 – y)
y = 150 – 3y
4y = 150
y = \frac{150}{ 4}
= 37.5
Distance of the point E from the pole AB is 37.5 meters.
7 (A)Select and write the most appropriate alternative from those provided in the brackets :
AP and AQ are the two tangent segments drawn from a point A to a circle with centre O.
if ∠PAQ = 60°, then ∠ POA = _____’
[ 30° , 60° , 90° , 120° ]
Ans : 60°
(B) A quadrilateral ABCD is drawn to circumscribe a circle as shown in the figure.
Prove that:
AB + DC = AD + BC
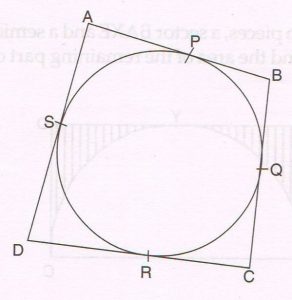
Ans : Proof:
We know that tangents segments, drawn from an external point, to a circle are equal in length.
AP = AS (from point A)
BP = BQ (from point B)
CR = CQ (from point C)
DR = DS (from point D)
Adding them we get
(AP + BP) + (CR + DR) = (AS + DS) + (BQ+ CQ)
AB + CD = AD + BC
(C ) Draw a circle with centre ’O’ and radius 2.5 cm. Then, take a point ‘A’ at a distance of 7 cm from the centre of the circle. Using a pair of compass and ruler construct two tangents AM and AN to the circle. Measure and state the length of the tangent segments.
Ans :
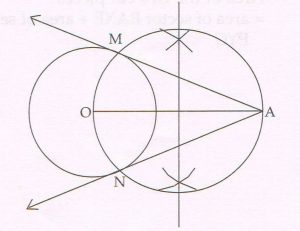
The length of each tangent segment is 6.7 cm
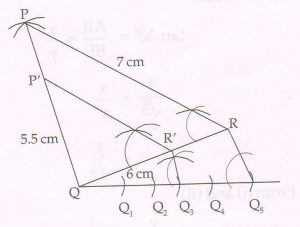
(D ) Using a pair of compass and ruler construct ΔPQR with sides PQ = 5.5 cm, QR = 6 cm and PR =7 cm. Then construct Δ P’QR’ ΔPQR whose sides are \frac{3}{ 5} of the corresponding sides of ΔPQR.
Ans :
8 ( A) Select and write the most appropriate alternative from those provided in the bracket :
1. The circumferences of two concentric circles are 8 π cm and 6 π cm. Therefore the distance between their radii is ___cm.
[ 48 , 14 , 2 , 1 ]
Ans : 1
1. The total surface area of a wooden cube is 5400 cm2. The length of its side is ____cm.
[ 54 , 34 , 30 , 20 ]
Ans : 30
(B) Attempt each of the following :
1. Find the area of a quadrant of a circle of diameter 28 cm ( Take π = \frac{22}{ 7} )
Ans : Area of quadrant = \frac{1}{ 4} πr2
= \frac{1}{ 4} × \frac{22}{ 7} × 14 × 14
= 154 cm2
2 . An open vessel is in the form of a hollow cylinder mounted on a hollow cone. The diameter and height of the cylinder are 10 cm each. The total height of the vessel is 22 cm. without substituting the value of π , find the outer curved surface area of the cylindrical part of the vessel.
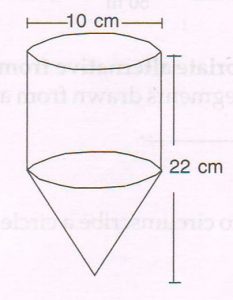
Ans : The outer curved surface area of the cylindrical part
= 2 π rh
= 2 × π × 5 × 10 sq. cm
= 100 π sq.cm
( C) From a rectangular metal sheet ABCD, two pieces, a sector BAXE and a semicircle EYC, each of radius 70 cm are cut off as shown in the figure. Find the area of the remaining part of the metal sheet shaded as shown in the figure. ( Take π = \frac{22}{ 7} )
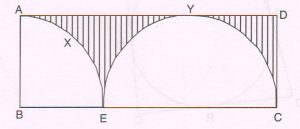
Ans : Area of the rectangular metal sheet ABCD
= AB × BC
= 70 × 210 sq. cm
= 14700 sq. cm … (1)
Area of the two cut pieces
= area of sector BAXE + area of semicircle EYC
= \frac{ø}{ 360} × πr2 + \frac{1}{ 2} × π r2
= ( \frac{90}{ 360} + \frac{1}{ 2} ) × πr2
= ( \frac{1}{ 4} + \frac{1}{ 2} ) × \frac{22}{ 7} × 70 × 70 sq. cm.
= \frac{3}{ 4} × 22 × 70 × 10
= 11550 sq cm … (2)
From (1) and (2), area of the remaining part left out
= (14700 − 11550 ) sq. cm.
= 3150 sq. cm
(D ) From a solid cylinder of height 30 cm and diameter 21 cm, two hemispherical cavities of the same diameter are hollowed out from either end. Find the volume of the remaining solid.
( Take π = \frac{22}{ 7} )
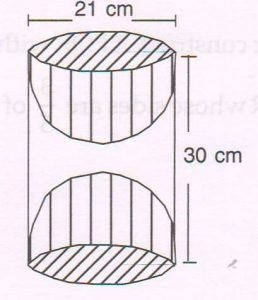
Ans : Volume of the solid cylinder
= π r2 h
= \frac{22}{ 7} × 10.5 × 10.5 × 30 cm3
= 22 × 1.5 × 1.5 × 315 cm3
= 10395 cm3 … (1)
Volume of the two hemispherical cavities
= Volume of one sphere
= \frac{4}{ 3} π r3
= \frac{4}{ 3}× \frac{22}{ 7} × 10.5 × 10.5 × 10.5 cm3
= 88 × 3.5 × 1.5 × 10.5 cm3
= 4851 cm3 … (2)
Volume of the remaining solid
= ( 10395 − 4851) cm3
= 5544 cm3
