GOA BOARD PAPER OCTOBER 2012
1(A) Select and write the most appropriate alternative from those provided in the bracket :
If two coins are tossed simultaneously, then the property of getting at least one tail is ___.
[ \frac{1}{4} , \frac{1}{2} , \frac{3}{4} , 1 ]
Ans : \frac{3}{4}
(B) A die is thrown once. Find the probability of getting :
1. A number less than 5
Ans : All possible outcomes are 6 in number. Favourable outcomes are 4 in number.
Probability of getting a number less then 5,
= \frac{4}{6} = \frac{2}{3}
2. A non prime number
Ans : Prime numbers are 2,3 and 5. Non-primes are 1 ,4 ,6.
Favourable outcomes = 6
Probability of getting a non-prime number
= \frac{3}{6} = \frac{1}{2} .
(C) Find the roots of ANY ONE of the following quadratic equations:
1. 3x2+ 14x +15 = 0
(By Factorisation Method)
Ans : 3x² +14x + 15x = 0
3x2+ 9x +5x + 15 = 0
3x (3x + 3) + 5 (x + 3) = 0
(x + 3) (3x + 5) = 0
either x + 3 = 0 OR 3x + 5 = 0
either x = −3 OR x= − \frac{5}{3}
Roots are −3 and − \frac{5}{3}
2. 4x² − 3x − 1 = 0 ( Portion deleted)
(By Completing the Square method)
Ans : 4x2 −3x − 1 = 0
Dividing by 4,
x² − \frac{3}{4} x = \frac{1}{4}
Adding \frac{9}{64} on both sides,
X2 − \frac{3}{4} x + \frac{9}{64} = \frac{1}{4} + \frac{9}{64}
[ x − \frac{3}{8} ]² = \frac{16 + 9}{64}
[ x − \frac{3}{8} ]² = \frac{25}{64}
Taking sq. root; i.e. x − \frac{3}{8} = ± \frac{5}{8}
Either x − \frac{3}{8} = \frac{5}{8} OR x − \frac{3}{8} = \frac{5}{8}
x = \frac{3 +5}{8} OR x = \frac{3 −5}{8}
x = 1 OR x = − \frac{1}{4}
Roots are 1 and − \frac{1}{4} .
(D) Riya’s mother is three years more than four times Riya’s age now. If the product of their ages is 280, find their present ages.
Ans : Let Riya’s present age be x years.
Then her mother’s age is 4x + 3 years.
Product of their ages = 280
x (4x +3) = 280
4x2 + 3x − 280 = 0
4x2 − 32x + 35x − 280 = 0
4x (x − 8) + 35 (x − 8) = 0
(x − 8) (4x + 35) = 0
x − 8 = 0 OR 4x + 35 = 0
x − 8 OR x = − \frac{35}{4}
As age cannot be a negative number, − \frac{35}{4} is discarded.
x = 8
Riya’s present age is 8 years, and her mother’s age is 4 × 8 + 3 = 35 years.
2(A) Select and write the most appropriate from those provided in the bracket :
If 3x + 2y = 16 and 2x + 3y = 19, then x + y = ____.
[ − 3 , 3 , 7 , 35 ]
Ans : 7
(B) The sum of the digit of a two-digit number is 9. Also, the difference between this number and the number obtained by reversing the order of the digits is 45. Represent the above statements by two linear equations in two variables.
Ans : Let the digit in the ten’s place be x
And the digit in the unit place be y.
The number is 10x + y
And the number with reversed digits is 10y + x
So the two equations are x + y = 9 ……..( 1 )
And (10x + y) − (10y + x) = 45.
10x + x − 10y + y = 45
11x − 9y = 45 ………………( 2 )
(C) Find the solution of ANY ONE of the following pair of linear equations :
1. 3x + 4y = 5 and 5x − 2y = − 9
(By elimination method)
Ans : 3x + 4y = 5 … (1)
5x − 2y = − 9 … (2)
Multiplying eq (2), by 2 we get
10x − 4y = − 18 … (3)
3x + 4y = 5 … (1)
———————-
13x + 4y = − 13
x = − 1
Subst. x= − 1 in Eq. (1),
3x (− 1) + 4y = 5
4y = 5 + 3
y = \frac{8}{4} = 2
The solution is x = − 1, y = 2
2. 7x + 2y = 20 and x + 2y = 8
(By substitution method)
Ans : 7x + 2y = 20 … (1)
x + 2y = 8
x = 8+2y … (2)
Substituting Eq 2 in (1), we get
7 ( 8 − 2y ) + 2y = 20
56 − 14y + 2y = 20
56 − 12y = 20
− 12y = 20 − 56
− 12y = − 36
y = \frac{36}{12} = 3
Substitute the value in Eq. (2),
x = 8 − ( 2 × 3)
x = 2
The solution is x = 2, y = 3
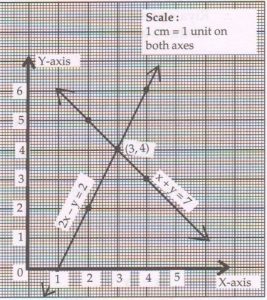
(D) Solve the following pair of linear equations graphically :
2x − y = 2 and x + y = 7
Rewrite and complete the following tables. Plot at least three points for each line using a graph paper.
2x − y = 2
| x | |||
| y |
x + y = 7
| x | |||
| y |
Ans :
y = 2x − 2
| x | 2 | 3 | 4 |
| y | 2 | 4 | 6 |
y = 7 − x
| x | 2 | 3 | 4 |
| y | 5 | 4 | 3 |
3(A) The product of two numbers is 304. If their H.C.F is 8 then their L.C.M is ____
[ 16 , 20 , 30 , 38 ]
Ans : 38
(B) The sum and product of the zeros of a quadratic polynomial are − \frac{4}{3} and \frac{5}{3} respectively. Comparing with the general form, find the values of a,b and c.
Hence write the quadratic polynomial in x.
Ans : Sum of the zeros = − \frac{a}{b} = − \frac{4}{3}
Product of the zeros = \frac{c}{a} = \frac{5}{3}
a = 3, b = 4, c = 5
The quadratic polynomial in x is 3x2 + 4x + 5
(C) If \sqrt{3} and − \sqrt{3} are two zeros of the polynomial x4 + 5x3 + 3x2 − 15x − 18, find the other two zeros.
Ans : Since \sqrt{3} and − \sqrt{3} are zeros of the polynomial.
To find other factors let us divide the polynomial by x2 − 3.
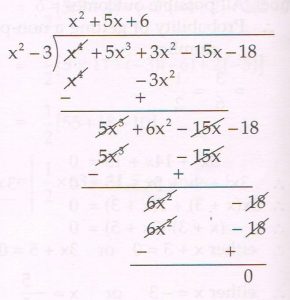
The other factor = x2 + 5x + 6
On factorising it, the factors are x + 2 and x + 3
So zeros are given by x + 2 = 0 and x + 3 = 0
i.e. x = − 2 and − 3.
The other two zeros are − 2 and − 3.
(D) Prove that \sqrt{5} is an irrational number.
Proof : Let us assume, to the contrary, that \sqrt{5} is rational.
We can find integers a and b (b ≠0) such that \sqrt{5} = \frac{a}{b} , where a and b are coprime.
b \sqrt{5} = a
Squaring both sides we get,
5b2 = a2 …. (1)
a2 is divisible by 5
a is divisible by 5 … (2)
Let a = 5c for some integer c … (3)
Substituting (3) in (1), we get
5b2 = (5c)2
5b2 = 25c2
b2 = 5c2
b2 is divisible by 5
b is divisible by 5. … (4)
From (2) and (4) a and b have a common factor 5.
This contradicts that a and b are coprime.
So Our assumption that \sqrt{5} is rational is wrong.
\sqrt{5} must be irrational.
4 (A) Select and write the most appropriate alternative from those provided in the bracket :
The 8th tern of an Arithmetic Progression whose first term is 10 and the common difference is − 5 is ____.
[ − 35 , − 25 , 25 , 35 ]
Ans : − 25
(B) The following table shows the ages of 38 members of a club:
|
Ages in years |
Number of members |
|
35 − 40 |
12 |
|
40 − 45 |
15 |
|
45 − 50 |
8 |
|
50 − 55 |
3 |
Find the mode of the given data.
Ans : Here the maximum frequency is 15,
The modal class = 40 − 45.
Where L = lower limit of the modal class=40
h = class size = 5
f1 = frequency of the modal class = 15
f0 = frequency of the class preceding the modal class = 12
f2 = frequency of the class succeeding the modal class = 8.
Mode = l + ( \frac{f1 + f0}{2f1 - f0- f2} ) × h
= 40 + ( \frac{15 - 12 }{2× 15-12-8} ) × 5
= 40 + ( \frac{3}{10} ) × 5
=40 + \frac{3}{2} = 40 + 1.5 = 41.5.
Mode of the given data is 41.5.
(C) Nita has to pay a sum of Rs.23,250 in 25 instalments such that each instalment is Rs. 40 more than the preceding one. Find the amount of the first and the last instalment.
Ans : Here S25 = 23250, n = 25 , d = 40. To find a and a25
Now Sn = \frac{n}{2} [ 2a + ( n − 1) d ]
S25 = \frac{25}{2} [ 2a + ( 25 − 1) × 40 ]
23250 = 25a +\frac{25}{2} × 24 × 40
23250 − 12000 = 25a
a = \frac{11250}{25} = 450 … (1)
Also an = a+ (n − 1) d
a25 = 450 + ( 25 − 1) 40
= 450 + 24 × 40
= 450 + 960
= 1410 … (2)
The first instalment = Rs 450
And the last instalment = Rs 1410.
(D) The following table shows the marks obtained by 50 students in Mathematics.
Taking the class-mark (denoted by ‘a’ ) of the class intervals 40 − 60 as the assumed mean, rewrite and complete the table, and also find the mean of the marks obtained.
Ans :
|
C.I |
fi |
xi |
di = xi−50 |
fidi |
|
0 − 20 |
8 |
10 |
−40 |
−320 |
|
20 − 40 |
16 |
30 |
−20 |
−320 |
|
40 − 60 |
20 |
50 |
0 |
0 |
|
60 − 80 |
6 |
70 |
20 |
120 |
|
Total |
∑fi= 50 |
|
|
∑fidi= 520 |
Mean = a + ∑ \frac{fi.di}{∑fi}
= 50 + − \frac{520}{50}
= 50 − 10.4
= 39.6
5(A) Select and write the most appropriate alternative from those provided in the bracket :
If sin 4 Ø = \frac{√3}{2} , then Ø = ______
Ans : 15°
(B) Attempt ANY ONE of the following :
1. In ΔPQR, ∠Q = 90°. If cot P = \frac{5}{12} , find
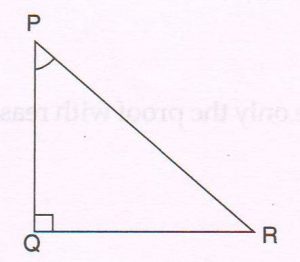
(a) the length of PR
(b) the value of sec R
(c) the value of sin P
Ans : (a) cot P= \frac{5}{12} = \frac{PQ}{QR}
By Pythagoras’ theorem,
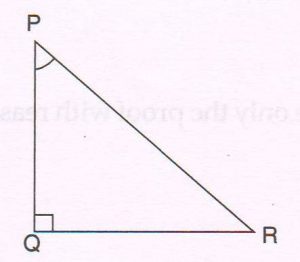
(PR)2 = (PQ)2+ (QR)2
= 52 + 122
= 25 + 144
= 169
PR = \sqrt{169} = 13
(b) sec R =\frac{1}{cos R} = \frac{1}{QR/PR} = \frac{13}{12}
(C) sin P = \frac{QR}{PR} = \frac{12}{13}
2. By substituting the known numerical values of trigonometric ratios evaluate the following :
\frac{2 tan²30° - sin² 60°}{3 cos²30°}
Ans :
\frac{2 tan^{2} 30° - sin^{2}60° }{3 cos^{2}30° } = \frac{2 × \big( \frac{1}{ \sqrt{3}})² - \big( \frac{ \sqrt{3} }{2} )²}{3 × \big( \frac{ \sqrt{3} }{2} )² }
= \frac{ \frac{2} {3} - \frac{3}{4} } {3 × \frac{3}{4} }
= \frac{ \frac{8 - 9}{12} }{ \frac{9}{4} }
= \frac{1}{12} × \frac{4}{9}
= − \frac{1}{27}
(C) In the figure, Δ ABC is a right-angled triangle, right-angled at B.
Prove that :
Sin2 Ø + cos2 ∅ = 1
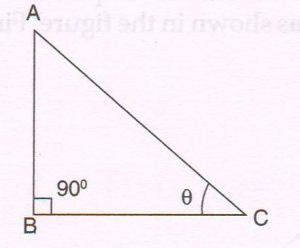
Ans : In ΔABC, right-angled a B, by Pythagoras theorem
(AB)2 + (BC)2 = (AC)2
Dividing each term by AC2, we get
\frac{AB²}{AC²} + \frac{BC²}{AC²} = \frac{AC²}{AC²}
( \frac{AB}{AC} )² + ( \frac{BC}{AC}² ) = 1 … (1)
Now \frac{AB}{AC} = sin ∅ and \frac{BC}{AC} = cos ∅ …. (2)
Using (2) and (1) , we get
(sin ∅ )2 + (cos ∅ ) = 1
sin2 ∅ + cos2 ∅ = 1
(D) Attempt each of the following :
1. Find the distance between the points ( −2 ,− 3) and ( 3, − 5).
Ans : By the distance formula, the distance between the points ( − 2, − 3) and ( 3, − 5) is
= \sqrt{(− 2 − 3)} + ( − 3 + 5)²
= \sqrt{(− 5)} + (2)²
= \sqrt{(25)} + 4
= \sqrt{(29)}
2. A point P (x , y) divides the segment joining the points ( − 1, − 2) and ( 4, −7) in the ratio 2 : 3. Find the values of x and y.
Ans : By section formula,
Coordinates of point are given by
( \frac{2 × 4 + 3 ( −1)}{2+3} ) , ( \frac{2 × ( −7 + 3 × (− 2))}{2+3} )
= ( \frac{8 - 3}{5} , \frac{− 20}{5} )
= ( \frac{5}{5} , \frac{− 20}{5}
= ( 1, − 4)
x = 1 and y = − 4
6(A) Select and write the most appropriate alternatives from those provided in the bracket :
DDEF ∼ ΔXYZ and DE : XY = 5 : 2. If the area of ΔDEF is 70cm2 , then the area of ΔXYZ = ____cm2.
[ 11 , 11.2 , 12 , 17.5 ]
Ans : 11.2
(B) In ΔABC, AC2 = AB2 + BC2 and Δ LMN is constructed such that LM = AB and MN = BC, ∠M = 90°.
Prove that : ΔABC is right-angled at B
(write only the proof with reasons.)
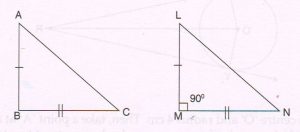
Proof: In ΔLMN, ∠M = 90° ( given)
(LN)2 = (LM)2 + (MN)2 (Pythagoras theorem) … (1)
Now, LM = AB and MN = BC (given)
From (1) , LN2 =AB2 + BC2 … (2)
But AB2 + BC2 = AC2 (given) … (3)
From (2) and (3), LN2 = AC2
LN = AC … (4)
In ΔABC and ΔLMN,
AB = LM (given)
BC = MN (given)
AC = LN (by (4) )
ΔABC ΔLMN (SSS Congruence rule)
∠B = ∠M (c.p.c.t)
But ∠M = 90° ∠B = 90°
ΔABC is right angled at B.
(C) In ΔABC, ∠B = 2 ∠C. if the bisector of ∠B meets side AC at D, then prove that:
\frac{BD}{DA} = \frac{CB}{BA}
(write only the proof with reasons)
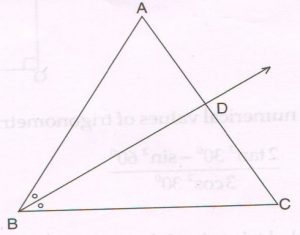
Proof : ∠ABD = ∠B (AD is the bisector)
= \frac{1}{2} × 2 × ∠C (given ∠B = 2 ∠C)
∠ABD = ∠C … (1)
In ΔABD and ΔACB
∠ABD = ∠C (by (1) )
∠A = ∠A (common angle)
ΔABD ≅ ΔACB (AA similarity criterion)
\frac{BD}{DA} = \frac{CB}{BA} (corresponding sides are proportional)
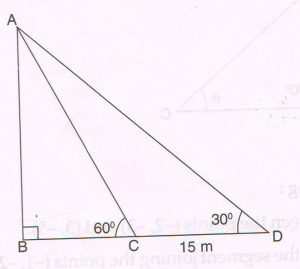
(D) From the points C and D on the ground which are 15m apart the angles of elevation to the top of a building AB are 60° and 30° respectively as shown in the figure. Find the height of the building AB.
BD = BC + CD = y + 15
In right. ΔABC, tan 60° = \frac{AB}{AC}
\sqrt{3} = \frac{x}{y}
x = y \sqrt{3} … (1)
In right ΔABD , tan 30° = \frac{AB}{BD}
\frac{1}{ \sqrt{3} } = \frac{x}{y + 15}
x = \frac{y + 15}{ \sqrt{3} } … (2)
From (1) and (2) we get
y \sqrt{3} = \frac{y + 15}{ \sqrt{3} }
3y = y + 15
2y = 15
y= \frac{15}{2} = 7.5.
From (1) We get x = 7.5 × \sqrt{3}
Height of the building = 7.5\sqrt{3} meters OR 7.5 × 1.73 = 12.975 meters.
7(A)Select and write the most appropriate alternative from those provided in the brackets :
Tangents SP and SQ from a point S to a circle with centre ‘O’ are inclined to each at an angle of 110°, then ∠SOP is equal to ____.
[ 35° , 70° , 80° , 110° ]
Ans : 35°
(B) ‘R’ is a point in the exterior of a circle with centre ‘O’ . RX and RY are two tangents at X and Y respectively. Prove that:
RX = RY
(write only the proof with reasons)
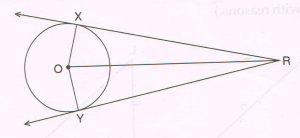
Proof: Since RX and RY are tangents to the circle at X and Y,
So they are perpendicular to the radius OX and OY respectively.
ΔOXR and ΔOYR are right-angled triangles at ∠x and ∠Y respectively.
OX = OY (radii of the same circle)
hyp. OR = hyp. OR (common side)
ΔOXR ≅ ΔOYR (RHS congruency)
RX = RY (c.p.c.t)
(C) Draw a circle with ‘O’ and radius 4 cm. Then, take a point ‘A’ at a distance of 9 cm from the centre of the circle. Using a pair of compasses and ruler construct two tangents AM and AN to the circle. Measure and state the length of the segments.
Ans :
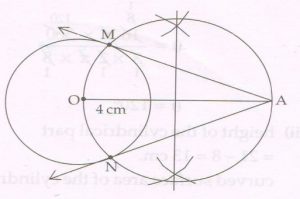
Length of each tangent segment is 8.1 cm.
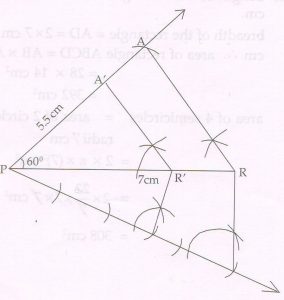
(D) Using a pair of compass and ruler construct ΔAPR with sides PR = 7 cm, PA =5.5 cm and ΔAPR = 60°. Then construct ΔA’PR’ whose sides are of the corresponding sides of ΔAPR.
Ans :
8(A) Select and write the most appropriate alternative from those provided in the brackets :
1. If the longest chord of a circle is 16.8 cm, then the radius of the circle is ___cm.
[ 4.2 , 8.4 , 14.8 , 12.6 ]
Ans : 8.4
2. The diameter of a cone and its height are respectively 10 cm and 12 cm. therefore the slant height of the cone is ___cm.
[ 13 , 16 , \sqrt{244}
Ans : 13
(B) Attempt each of the following :
1.O is the centre of a circle of radius 8 cm. Arc AXB of the circle, of length \frac{16π}{3} cm subtends ∠AOB at the centre. Find the measure of ∠AOB
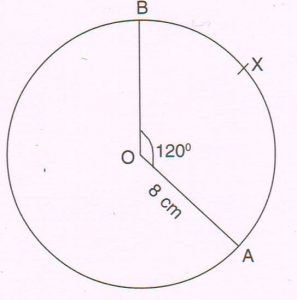
Ans :
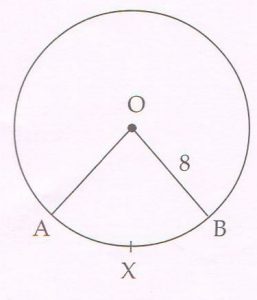
Length of arc = \frac{ø}{360} × 2πr
\frac{16π}{3} = \frac{ø}{360} × 2π × 8
ø = \frac{16π × 360}{3 ×2π × 8}
ø = ∠AOB = 120°
2. An object is in the shape of a cylinder surmounted by a hemisphere. The radius of the base of the cylindrical part is 8 cm and the height of the object is 21 cm.
Find : The curved surface area of the cylindrical part.
(Do not substitute the value of π )
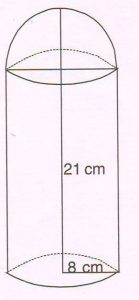
Ans : Height of the cylindrical part
= 21 − 8 = 13 cm.
Curved surface area of cylindrical part
= 2πrh = 2 × π × 8 × 13 cm2
208π cm2
(C) ABCD is a rectangle, four semicircles each of diameter 14 cm are drawn as shown in the figure. Find the area of the shaded region.

Ans : Length of the rectangle = AB = 14 + 14 = 28 cm.
Breadth of the rectangle = AD = 2 7 cm = 14 cm
Area of rectangle ABCD = AB x AD
= 28 x 14cm2
=392cm2 … (1)
Area of 4 semicircle = area of 2 circles of radii 7cm
= 2 × π × (7)2 cm2
= 2 × \frac{22}{7} × 7 × 7 cm2
= 308 cm2 … (2)
Area of the shaded region
= (392 − 308) cm2 (from (1) and (2) )
= 84 cm2
(D) A conical vessel whose internal radius is 15.4 cm and height is 21 cm is filled with water. The water is then poured into a cylinder with internal radius 7 cm. Find the height of water level in the cylinder.
(Take π = \frac{12}{7} )
Ans : Volume of water in the conical vessel = volume of water in the cylinder.
Let R and H be the radius and height of water in the conical vessel.
Let r and h be the radius and height of water in the cylinder.
Then \frac{1}{3} π R2H = πr2h
\frac{1}{3} π 15.4 × 15.4 × 21 = π × 7 × 7 × h
\frac{15.4 ×15.4 ×7}{7 × 7} = h
h = 15.4 × 2.2
= 33. 88 cm
Height of water in the cylinder is 33.88 cm.