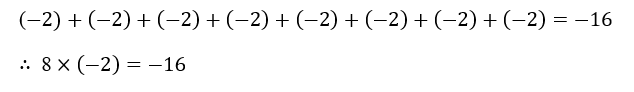1.2 PROPERTIES OF INTEGERS:
The sum of any two integers is always an integer. Integers are closed under addition.
For any two integers a and b, a + b is an integer.
If a and b are any two integers, then a + b = b + a
If a,b,c are any three integers, then (a + b) + c = a + (b + c)
If ‘a’ is any integer, then a + 0 = a or 0 + a. Zero is additive identity for integers.
The sum of an integer and its opposite is 0. Thus , if ‘a’ is an integer, then a + (−a) = 0
If ‘a’ and ‘b’ are any two integers and a − b = c, then ‘c’ is also an integer.
If ‘a’ is an integer. then (a−1) is its predecessor.
If ‘a’ is any integer , then a−o =a, i.e., zero subtracted from any integer is the integer itself.
Exercise 1.2
- Write down a pair of integers whose:
- a) Sum is – 7 b) Difference is – 10 c) Sum is 0
Solution: a) We can have (– 3) + (– 4) =– 7
The required pair of integers is – 3 and – 4
b) We can have – 16 – (– 6) = – 16 + 6 = – 10
The required pair of integers is – 16 and – 6
c) We can have – 8 + 8 = 0
The required pair of integers is – 8 and 8
2.a) Write a pair of negative integers whose difference gives 8 b) Write a negative integer and a positive integer whose sum is –5 c) Write a negative integer and a positive integer whose difference is – 3.
Solution: a) Since, –7 –( –15) = –7 + 15 = 8
So, – 7 and 15 is a pair of negative integers such that their difference is 8.
b) Since, (– 6) + 1 = –5
So, – 6 and 1 is a pair of integers such that their sum is – 5 and one of them is a negative integer.
c) Since, –9 –( – 6) = –9 + 6 = – 3
So, – 9 and – 6 are a pair of integers such that their difference is – 3 and one of them is positive and other is negative.
3.In a quiz, team A scored – 40, 10, 0 and team B scored 10, 0, – 40 in three successive rounds. Which team scored more? Can we say that we can add integers in any order?
Solution:- Total score obtained by team A = – 40 + 10 + 0
= – 40 + 10 = – 30
Total Score of team B = 10, 0, −40
Total score obtained by team B = 10 + 0 + (– 40)
= 10 + 0 – 40 = – 30
Therefore, scores of the both A team and B team are same. – 30.
Yes, we can say that we can add integers in any order.
4.Fill in the blanks to make the following statements true:
(i) (–5) + (– 8) = (– 8) + (…………)
(ii) –53 + ………… = –53
(iii) 17 + ………… = 0
(iv) [13 + (– 12)] + (…………) = 13 + [(–12) + (–7)]
(v) (– 4) + [15 + (–3)] = [– 4 + 15] +…………
Solution:-
i) Since, integers can be added in any order, (– 5) + (– 8) = (– 8) + (– 5)
ii) If we add zero to any integer, we get the same integer. – 53 + 0 = – 53
iii) We know that the sum of an integer and its additive inverse is zero. 17 + (– 17) = 0
iv) Since, the addition of integers is associative. For three integers, a, b, and c, we have: ( a + b) + c = a + (b + c) Thus, [13 + (– 12)] + (– 7) = 13 + [(–12) + (–7)]
v) (– 4) + [15 + (–3)] = [– 4 + 15] + (–3)
( –4) + [15 –3] = [ 11] – 3
– 4 +12 = 11 – 3
8 = 8
Try these: (page 10)
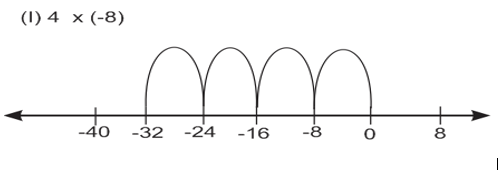
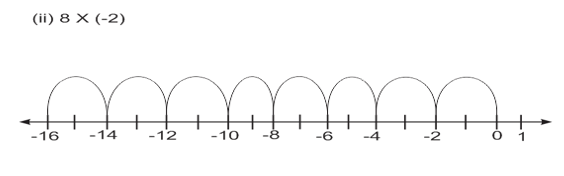
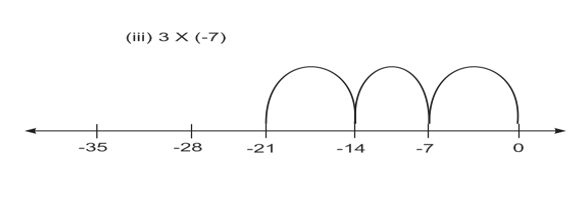
Q.1) Using number line, find:
(i) 4 x ( –8) (ii) 8 x (–2) (iii) 3 (iv) 10
Solution:
From the number line, we have:
(8) (8) (8) (8) = 32
∴ 4 x (–8) = 32
From the number line, we have:
From the number line, we find:
(7) + (7) + (7) = 21
From the number line, we have:
(–1)+ (–1) +(–1) +(–1)+ (–1) +(–1) +(–1)+ (–1) +(–1) +(–1) = –10
Try these: (page 10)
i) 6 ×–19 ii) 12 ×–32 iii) 7 × –22
Solution:
i) 6 × –19= – [6 × 19] = –114
ii) 12 ×–32 = – [12 × 32] = –384
iii) 7 ×–22 = – [7 × 22] = –154
Try these: (page 11)
a) 15 × ( –16) b) 21× ( –32) c) (–42) × 12 d) (–55)× 15
Solution:
While multiplying a positive integer and a negative integer, we multiply them first and put a minus sign (–) before the product.
a) 15 × (– 16) = [15 × –16] = –240
b) 21 ×–32 = [21 ×–32 ] = –672
c) (–42)× 12 = –[42 ×12] = –504
d) (–55) ×15 = –[55 ×15]= –82
Try these: (page 12)
1) Find: (–31)(–100), (–25)(–72), (–83)(–28)
Solution: We multiply the two negative integers and put the positive sign(+) before the product.
(–31)×(–100) = [ –31×–100] = + 3100
(–25)×(–72) = [–25 ×–72] = +1800
(–83)×(–28) = [–83 ×–28] = +2324
Try these: (page 18)
i) Is 10 x [6 + (−2)] = 10 x 6 + 10 x (−2)
ii) Is (−15) x [(−7) + (−1)] = (-15) x (-7) + (−15) x (−1)
Solution:
i) [ a x (b + c) = a x b + a x c]
10 x [ 6 + (−2) ] = 10 x [ 6 − 2 ]
= 10 x 4 = 40
And, 10 x 6 + 10 x (−2) = 60 − 20 = 40.
Thus, 10 x [6 + ( –2)] = 10 x 6 + 10 ( –2)
(ii) [ a x ( b + c ) = a x b + a x c]
( –15) x [ –(7) + ( –1) = ( –15 ) x [ –7 –1 ]
= ( –15 ) x ( –8 )
= ( + ) ( 15 x 8 ) = 120.
And, ( – 15 ) x ( – 7 ) + ( – 15 ) x ( –1 )
= (+) ( 15 x 7 ) + ( + ) ( 15 x 1 )
= 105 + 15 = 120.
Thus, ( – 15 ) x (–7) + ( – 1 ) =(–15) x (7) + (–15) x (–1)
Try these: (Page 19)
By using distributive property find: i) (– 49 ) x 18; ii) (–25) x (–31); iii) 70 x (–19) + (–1) x 70
Solution:
i) ( – 49 ) x 18:
18 = 10 + 8
( –49 ) x 18
= ( – 49 ) x [10 x 8 ]
= ( –49 ) x 10 + ( –49 ) x 8
Using Distributive Property we get
= – 490 + ( –49 ) [ 10 – 2 ] because [ 8 = 10 –2 ]
= − 490 + ( – 49 ) x 10 – ( –49 ) x 2
= 490 + (– 490 ) + 98
= –980 + 98 = 882
(ii) ( –25 ) x (–31):
–31 = ( –30 ) + ( – 1 )
( –25 ) x ( –31 )
= ( – 25 ) x [ ( –30 ) + (–1) ]
= (–25 ) x ( –30 ) + ( –25) x (–1)
using Distributive Property
= + ( 25 x 30 ) + [ (25 x 1) ]
= 750 + 25 = 775
(iii) 70 x ( –19 ) + ( –1 ) x 70 :
a × b + a × c = a × [ b + c ]
70 × ( –19 ) + (– 1 ) × 70
= 70 × [ ( 19 ) + (–1) ]
= 70 × [ – 20 ] = [ 70 × 20 ] = –1400